Usuario:


Aumento del nivel del mar
Imagen

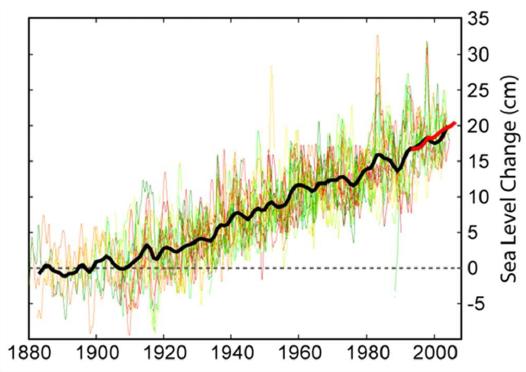
Desde 1900 se observa un continuo incremento del nivel del mar que suma actualmente sobre 20,cm:

Aumento del nivel del mar

ID:(7412, 0)


Mecánica del aumento del nivel por deshielo
Imagen

El hielo y nieve se derrite y fluye como agua al mar haciendo subir el nivel de este:

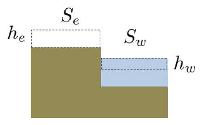
Aumento del nivel del mar por deshielo

ID:(7414, 0)


Distribución del aumento de nivel del mar
Imagen

El aumento del nivel del mar se concentra en las zonas ecuatoriales y en un \'cinturon\' en el hemisferio sur:

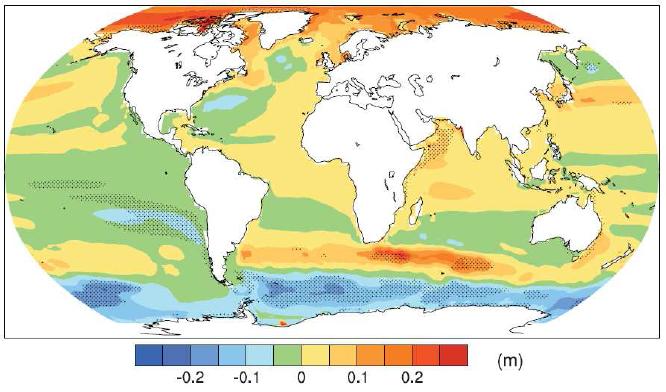
Variación del nivel del mar

ID:(7413, 0)


Profundidad del mar ante escenarios de deshielo
Descripción

Si se aplica esta ecuación a las masas de hielo que existen sobre el planeta se obtienen las siguientes aumentos de profundidad:Hielo | Área [$10^6km^2$] | Volumen[$10^6km^3$ ] | Aumento [$m$]--------|:--------:|:---------:|:-------:Nieves HN | $1,9-25,2$ | $5?imes 10^{-4}-5\times 10^{-3}$ | $10^{-3}-10^{-2}$Hielo en mar | $19-27$ | $0.019-0.025$ | $0$Glaciares | $0,51-0,54$ | $0.05-0.13$ | $0.15-0.37$Groenlandia | $1,7$ |$2.9$ | $7.3$Antártica | $12,3$ | $24.7$ | $56.6$El hielo que esta en el mar no contribuye en aumento del nivel pues el volumen desplazado por el hielo es igual al que luego ocupa el agua derretida.

ID:(7436, 0)


Nivel del Mar
Descripción

ID:(96, 0)


Nivel del mar en el pasado
Imagen

La ultima edad de hielo significo que los mares bajaran hasta 120 metros del nivel del actual:

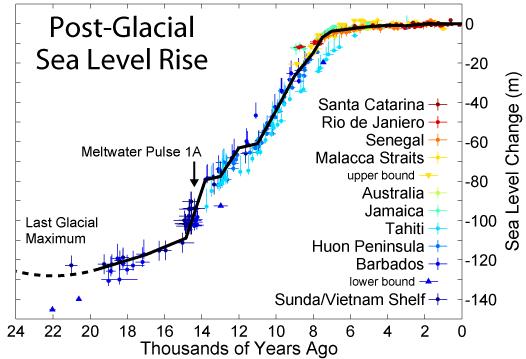
Nivel del mar en el pasado

ID:(7428, 0)


Tendencia en el cambio de nivel del mar
Imagen

La tendencia del nivel del mar calculado entre 1993 y 2008 muestra zonas en que hay aumentos de 5-10 mm/años mientras que en otros hay una reducción entre 0-5 mm/años:

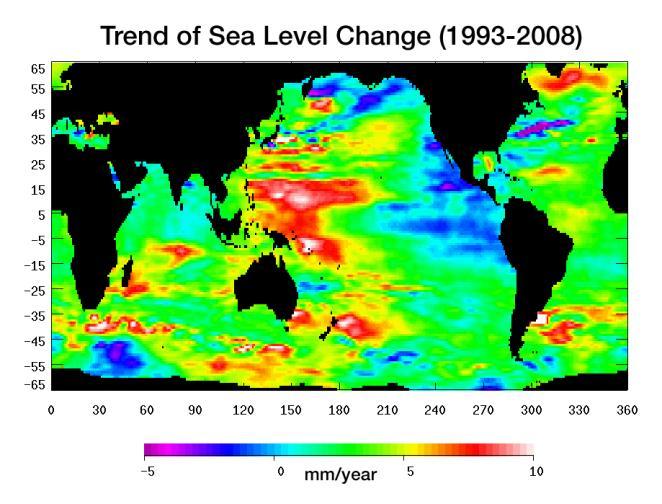
Tendencia en nivel del mar

ID:(7427, 0)


Nivel del mar en Valdivia (sin subida del mar)
Imagen

Visualización de la situación de Valdivia con un aumento en 0 metros del nivel del mar:

Valdivia, 0 metros nivel del mar

ID:(7417, 0)


Nivel del mar en Valdivia (1 metro)
Imagen

Visualización de la situación de Valdivia con un aumento en 1 metro del nivel del mar:

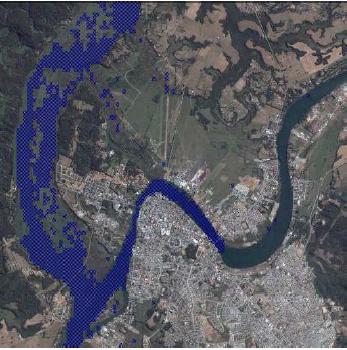
Valdivia, subida en 1 metro

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

ID:(7418, 0)


Nivel del mar en Valdivia (3 metros)
Imagen

Visualización de la situación de Valdivia con un aumento en 3 metros del nivel del mar:

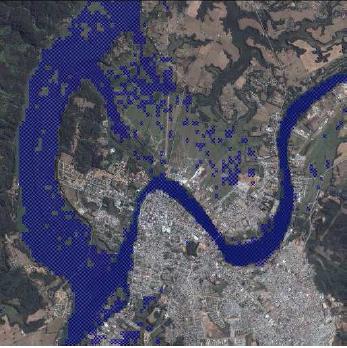
Valdivia, subida en 3 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

ID:(7419, 0)


Nivel del mar en Valdivia (6 metros)
Imagen

Visualización de la situación de Valdivia con un aumento en 6 metros del nivel del mar:

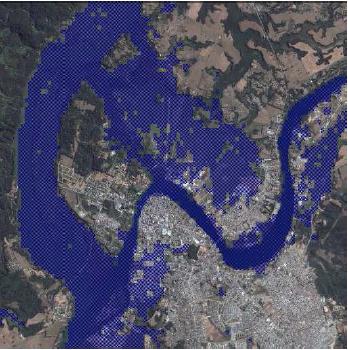
Valdivia, subida en 6 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

ID:(7420, 0)


Nivel del mar en Valdivia (10 metros)
Imagen

Visualización de la situación de Valdivia con un aumento en 10 metros del nivel del mar:

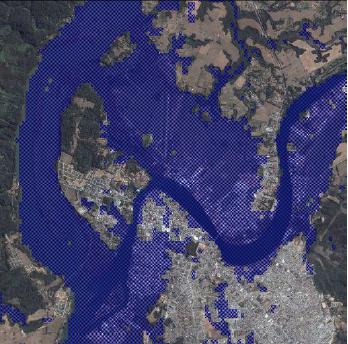
Valdivia, subida en 10 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

ID:(7421, 0)


Nivel del mar en Valdivia (14 metros)
Imagen

Visualización de la situación de Valdivia con un aumento en 14 metros del nivel del mar:

Valdivia, subida en 14 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

ID:(7422, 0)


Teoría de la Isostasia
Imagen

La hipótesis de la isostasia de que los deshielo no contribuyen al aumento del nivel del mar se basa en que la perdida de hielo y nieve lleva a que el contiene pierde masa y flota mas sobre el magma:

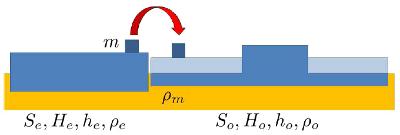
Hipótesis de la isostasia

Al descargar el hielo desde una placa, esta asciende, mientras que la que recibe el peso adicional se hunde. La pregunta es si y como afectaría la subida del mar por el calentamiento global.

ID:(7415, 0)


Estructura de los continentes
Imagen

Uno de los problemas de la teoría de la isostasia es que no existe esa separación contienente-placa submarina lo que implicaría que se debe modelar como un continuo con deformaciones lo que reduce el efecto.

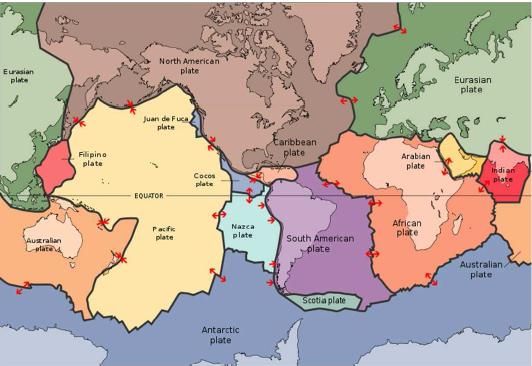
Placas continentales

ID:(7416, 0)


Cálculo en el caso de existir Isostasia
Descripción

Para calcular la altura con que se hunde la placa que carga la masa de hielo h_e , se debe calcular la fuerza gravitacional e igualarla a la fuerza de sustentación que da el magma. La fuerza gravitacional se calcula de la masa total compuesta por el hielo m y aquella de la placa calculada de la densidad \rho_e con una superficie S_e y una altura H_e y la aceleración gravitacional g. La sustentación a su vez depende de la altura hundida h_e y de la densidad del magma \rho_m . De esta forma se tiene la ecuación(S_eH_e\rho_e + m)g = S_eh_e\rho_mSi se despeja la altura que se hunde la placa se obtieneh_e=\displaystyle\frac{\rho_e}{\rho_m}H_e+\displaystyle\frac{m}{S_e\rho_m}Al derretirse la masa de hielo y abandonar la placa la nueva profundidad sera aquella que se calcula con la ecuación anterior para el caso m = 0 o seah_e\'=\displaystyle\frac{\rho_e}{\rho_m}H_eLa altura total que sube el continente es por ello\Delta h_e=h_e-h_e\'=\displaystyle\frac{m}{S_e\rho_m}A su vez la placa que recibe el peso adicional esta hundida a una profundidad deh_0 =\displaystyle\frac{\rho_0}{\rho_m}H_0donde \rho_0 es la densidad y H_0 la altura de dicha placa. En este caso al recibir la segunda placa el peso adicional se hundiría hasta una profundidad deh_0=\displaystyle\frac{\rho_0}{\rho_m}H_0+\displaystyle\frac{m}{S_0\rho_m}De este modo el cambio de profundidad de la segunda placa es de\Delta h_0=h_0-h_0\'=\displaystyle\frac{m}{S_0\rho_m}Por ello la diferencia efectiva entre ambas placas sera la suma de ambos desplazamientos, es decir\Delta_h=\Delta h_e+\Delta h_0=\displaystyle\frac{m}{\rho_m}\left(\displaystyle\frac{1}{S_e}+\displaystyle\frac{1}{S_0}\right)Si expresamos la masa de hielo en función de la variación de la profundidad del nivel del mar h_w tendremos quem=S_0h_w\rho_wdonde \rho_w es la densidad del agua. En este caso la variación total de alturas sera de\Delta h = h_w\displaystyle\frac{\rho_w}{\rho_mm}\left(1+\displaystyle\frac{S_0}{S_e}\right)Como el agua misma sube el nivel del mar sube en h_w , respecto del continente en que se encontraba el hielo la variación del nivel del mar seria por\Delta h_w=\Delta h-h_w=h_w\left(\displaystyle\frac{\rho_w}{\rho_m}\left(1+\displaystyle\frac{S_0}{S_e}\right)-1\right)Si se asume que la densidad del agua es de 1,g/cm^3, la del magma 3.2,g/cm^3 y el mar ocupa el 70\% de la superficie terrestre se llega a la relación\Delta h_w = 0.04167 h_wo sea que el nivel de subida de los océanos seria solo una fracción por el hecho que los continentes subirían y el mar a su vez se hundiría.Con los 20 cm que ha subido el mar en los últimos 150 años se concluiría que si existiese isostasia la capa de hielo que ya se habría derretido tendría una altura de 4.7,m lo que implicaría que no se observa el fenómeno.

ID:(7437, 0)


Efectos sobre el nivel del mar
Modelo

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$h_w$
h_w
Altura adicional nivel del Mar por deshielos
m
$h_e$
h_e
Altura capa de Hielo
m
$\Delta l$
dl
Aumento de Profundidad por Dilatación termica
m
$\alpha$
alpha
Coeficiente de dilatación del Agua
1/K
$\rho_w$
rho_w
Densidad del agua
kg/m^3
$\rho_e$
rho_e
Densidad del Hielo
kg/m^3
$l$
l
Profundidad del Mar
m
$S_e$
S_e
Superficie con Hielo a derretir
m^2
$S_w$
S_w
Superficie de Mares
m^2
$\Delta T$
DT
Variación de Temperature
K

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Desde 1900 se observa un continuo incremento del nivel del mar que suma actualmente sobre 20,cm:

Aumento del nivel del mar

(ID 7412)

El hielo y nieve se derrite y fluye como agua al mar haciendo subir el nivel de este:

Aumento del nivel del mar por deshielo

(ID 7414)

El aumento del nivel del mar se concentra en las zonas ecuatoriales y en un \'cinturon\' en el hemisferio sur:

Variaci n del nivel del mar

(ID 7413)

Si se aplica esta ecuaci n a las masas de hielo que existen sobre el planeta se obtienen las siguientes aumentos de profundidad:Hielo | rea [$10^6km^2$] | Volumen[$10^6km^3$ ] | Aumento [$m$]--------|:--------:|:---------:|:-------:Nieves HN | $1,9-25,2$ | $5?imes 10^{-4}-5\times 10^{-3}$ | $10^{-3}-10^{-2}$Hielo en mar | $19-27$ | $0.019-0.025$ | $0$Glaciares | $0,51-0,54$ | $0.05-0.13$ | $0.15-0.37$Groenlandia | $1,7$ |$2.9$ | $7.3$Ant rtica | $12,3$ | $24.7$ | $56.6$El hielo que esta en el mar no contribuye en aumento del nivel pues el volumen desplazado por el hielo es igual al que luego ocupa el agua derretida.

(ID 7436)

La ultima edad de hielo significo que los mares bajaran hasta 120 metros del nivel del actual:

Nivel del mar en el pasado

(ID 7428)

La tendencia del nivel del mar calculado entre 1993 y 2008 muestra zonas en que hay aumentos de 5-10 mm/a os mientras que en otros hay una reducci n entre 0-5 mm/a os:

Tendencia en nivel del mar

(ID 7427)

Visualizaci n de la situaci n de Valdivia con un aumento en 0 metros del nivel del mar:

Valdivia, 0 metros nivel del mar

(ID 7417)

Visualizaci n de la situaci n de Valdivia con un aumento en 1 metro del nivel del mar:

Valdivia, subida en 1 metro

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

(ID 7418)

Visualizaci n de la situaci n de Valdivia con un aumento en 3 metros del nivel del mar:

Valdivia, subida en 3 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

(ID 7419)

Visualizaci n de la situaci n de Valdivia con un aumento en 6 metros del nivel del mar:

Valdivia, subida en 6 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

(ID 7420)

Visualizaci n de la situaci n de Valdivia con un aumento en 10 metros del nivel del mar:

Valdivia, subida en 10 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

(ID 7421)

Visualizaci n de la situaci n de Valdivia con un aumento en 14 metros del nivel del mar:

Valdivia, subida en 14 metros

Calculado con el simulador de nivel del mar [http://flood.firetree.net/](http://flood.firetree.net/).

(ID 7422)

La hip tesis de la isostasia de que los deshielo no contribuyen al aumento del nivel del mar se basa en que la perdida de hielo y nieve lleva a que el contiene pierde masa y flota mas sobre el magma:

Hip tesis de la isostasia

Al descargar el hielo desde una placa, esta asciende, mientras que la que recibe el peso adicional se hunde. La pregunta es si y como afectar a la subida del mar por el calentamiento global.

(ID 7415)

Uno de los problemas de la teor a de la isostasia es que no existe esa separaci n contienente-placa submarina lo que implicar a que se debe modelar como un continuo con deformaciones lo que reduce el efecto.

Placas continentales

(ID 7416)

Para calcular la altura con que se hunde la placa que carga la masa de hielo h_e , se debe calcular la fuerza gravitacional e igualarla a la fuerza de sustentaci n que da el magma. La fuerza gravitacional se calcula de la masa total compuesta por el hielo m y aquella de la placa calculada de la densidad \rho_e con una superficie S_e y una altura H_e y la aceleraci n gravitacional g. La sustentaci n a su vez depende de la altura hundida h_e y de la densidad del magma \rho_m . De esta forma se tiene la ecuaci n(S_eH_e\rho_e + m)g = S_eh_e\rho_mSi se despeja la altura que se hunde la placa se obtieneh_e=\displaystyle\frac{\rho_e}{\rho_m}H_e+\displaystyle\frac{m}{S_e\rho_m}Al derretirse la masa de hielo y abandonar la placa la nueva profundidad sera aquella que se calcula con la ecuaci n anterior para el caso m = 0 o seah_e\'=\displaystyle\frac{\rho_e}{\rho_m}H_eLa altura total que sube el continente es por ello\Delta h_e=h_e-h_e\'=\displaystyle\frac{m}{S_e\rho_m}A su vez la placa que recibe el peso adicional esta hundida a una profundidad deh_0 =\displaystyle\frac{\rho_0}{\rho_m}H_0donde \rho_0 es la densidad y H_0 la altura de dicha placa. En este caso al recibir la segunda placa el peso adicional se hundir a hasta una profundidad deh_0=\displaystyle\frac{\rho_0}{\rho_m}H_0+\displaystyle\frac{m}{S_0\rho_m}De este modo el cambio de profundidad de la segunda placa es de\Delta h_0=h_0-h_0\'=\displaystyle\frac{m}{S_0\rho_m}Por ello la diferencia efectiva entre ambas placas sera la suma de ambos desplazamientos, es decir\Delta_h=\Delta h_e+\Delta h_0=\displaystyle\frac{m}{\rho_m}\left(\displaystyle\frac{1}{S_e}+\displaystyle\frac{1}{S_0}\right)Si expresamos la masa de hielo en funci n de la variaci n de la profundidad del nivel del mar h_w tendremos quem=S_0h_w\rho_wdonde \rho_w es la densidad del agua. En este caso la variaci n total de alturas sera de\Delta h = h_w\displaystyle\frac{\rho_w}{\rho_mm}\left(1+\displaystyle\frac{S_0}{S_e}\right)Como el agua misma sube el nivel del mar sube en h_w , respecto del continente en que se encontraba el hielo la variaci n del nivel del mar seria por\Delta h_w=\Delta h-h_w=h_w\left(\displaystyle\frac{\rho_w}{\rho_m}\left(1+\displaystyle\frac{S_0}{S_e}\right)-1\right)Si se asume que la densidad del agua es de 1,g/cm^3, la del magma 3.2,g/cm^3 y el mar ocupa el 70\% de la superficie terrestre se llega a la relaci n\Delta h_w = 0.04167 h_wo sea que el nivel de subida de los oc anos seria solo una fracci n por el hecho que los continentes subir an y el mar a su vez se hundir a.Con los 20 cm que ha subido el mar en los ltimos 150 a os se concluir a que si existiese isostasia la capa de hielo que ya se habr a derretido tendr a una altura de 4.7,m lo que implicar a que no se observa el fen meno.

(ID 7437)

ID:(583, 0)