Druyd:Knowledge

Modelo 1D

Storyboard

>Modelo

ID:(1037, 0)

Simplificación del Modelo

Imagen

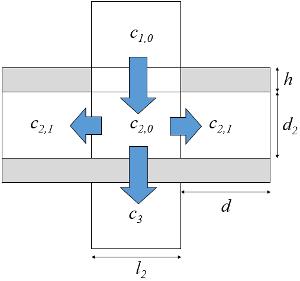
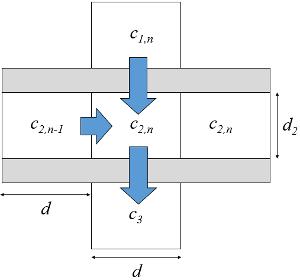
Lo angosto de la cavidad entre membranas muestra que el sistema se comporta como un sistema de conductores paralelos:

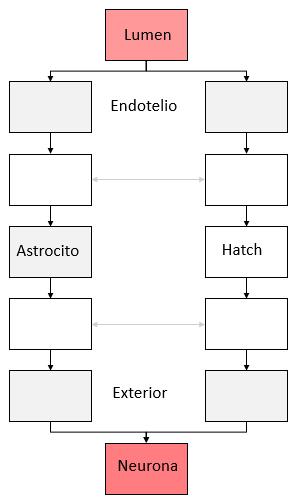
La interacción entre ambos conductores solo es relevante en procesos muy lentos (minutos) ya que depende de la difusión perimetral que es muy lenta ($D$).

ID:(8763, 0)

Flujo para $c_1$ en $0 < s < n$

Imagen

ID:(8890, 0)

Flujo para $c_1$ en $s=0$

Imagen

ID:(8892, 0)

Flujo para $c_1$ en $s=n$

Imagen

ID:(8894, 0)

Flujo para $c_2$ en $0 < s < n$

Imagen

ID:(8891, 0)

Flujo para $c_2$ en $s=0$

Imagen

ID:(8893, 0)

Flujo para $c_2$ en $s=n$

Imagen

ID:(8895, 0)

Solución Constante

Descripción

Si se asumen $c_0$ y $c_3$ constantes tanto en el tiempo como en el perímetro se tiene que las ecuaciones

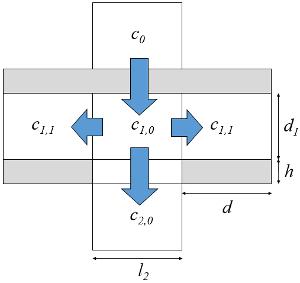
$\displaystyle\frac{d}{dt}c_{1,0}=\displaystyle\frac{1}{2\pi Rd_1}j(j_{s0},c_{s0},c_0,c_{1,0})+\displaystyle\frac{2}{dl_2}D(c_{1,1}-c_{1,0})-\displaystyle\frac{1}{hd_1}D(c_{1,0}-c_{2,0})$

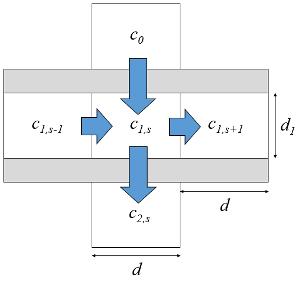
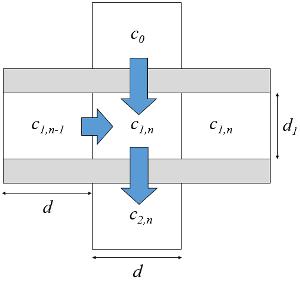
$\displaystyle\frac{d}{dt}c_{1,s}=\displaystyle\frac{1}{2\pi Rd_1}j(j_{s0},c_{s0},c_0,c_{1,s})-j(j_{s1},c_{s1},c_{1,s},c_{2,s}))+\displaystyle\frac{1}{d^2}D(c_{1,s+1}+c_{1,s-1}-2c_{1,s})$

implican que las soluciones para $c_{1,s}$ y $c_{2,s}$ se pueden escribir como una constante mas una parte que puede depender de la posición y/o del tiempo:$c_{1,s}=c_1^0+c_1(s,t)$y$c_{2,s}=c_2^0+c_2(s,t)$Introduciendo ambas soluciones en las ecuaciones anteriores se tiene que se pueden elegir $c_1^0$ y $c_2^0$ de modo que $c_1(s,t)$ y $c_2(s,t)$ ya no dependen de $c_0$ y $c_3$. Esto se da si$D_{s0}(c_0-c_1^0)-D_{s1}(c_1^0-c_2^0)=0$y$D_{s0}(c_1^0-c_2^0)-D_{s1}(c_2^0-c_3)=0$

ID:(8896, 0)

Dependencia Espacial

Descripción

Para el caso estacionario las ecuaciones de la parte de la solución que dependen del perímetro se obtienen de

$\displaystyle\frac{\partial c_{1,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_1}(D_{s0}(c_0-c_{1,s})-D_{s1}(c_{1,s}-c_{2,s}))+D\displaystyle\frac{\partial^2c_{1,s}}{\partial s^2}$

$\displaystyle\frac{\partial c_{2,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_2}(D_{s0}(c_{1,s}-c_{2,s})-D_{s1}(c_{2,s}-c_3))+D\displaystyle\frac{\partial^2c_{2,s}}{\partial s^2}$

siendo$\displaystyle\frac{d^2}{ds^2}c_{1,s}=\displaystyle\frac{1}{2\pi Rd_1}\displaystyle\frac{(D_{s0}+D_{s1})}{D}c_{1,s}-\displaystyle\frac{1}{2\pi Rd_1}\displaystyle\frac{D_{s1}}{D}c_{2,s}$y$\displaystyle\frac{d^2}{ds^2}c_{2,s}=\displaystyle\frac{1}{2\pi Rd_2}\displaystyle\frac{(D_{s0}+D_{s1})}{D}c_{2,s}-\displaystyle\frac{1}{2\pi Rd_2}\displaystyle\frac{D_{s0}}{D}c_{1,s}$La solución tiene la forma$c_{1,s}=A_1e^{ks}$y$c_{2,s}=A_2e^{ks}$Si se introduce esta solución en la ecuación se obtiene que $k$ debe satisfacer:$(D_{s0}+D_{s1}-2\pi Rd_1Dk^2)(D_{s0}+D_{s1}-2\pi Rd_2Dk^2)=D_{s0}D_{s1}$

ID:(8931, 0)

Solución Perimetral

Descripción

Como el vector de onda es positivo la solución es una suma de exponenciales $e^{ks}$ y $e^{-ks}$. Por otro lado, como debe ser simetrica respecto del origen en $s=0$ y continua en el otro extremo $s=\pi R$ se debe tener que la pendiente en dicho punto debe ser nula. Por ello la solución debe corresponder a un coseno hiperbolico. Si se considera el factor constante antes calculado será de la forma

$c_1(s)=c_1^0+(c_{1,0}-c_1^0)\displaystyle\frac{\cosh k(\pi R - s)}{\cosh k\pi R}$

y

$c_2(s)=c_2^0+(c_{2,0}-c_2^0)\displaystyle\frac{\cosh k(\pi R - s)}{\cosh k\pi R}$

donde $c_{1,0}$ y $c_{2,0}$ son las concentraciones frente al hatch. Para calcular ambas concentraciones basta con reemplazar las funciones en

$\displaystyle\frac{\partial c_{1,0}}{\partial t}=\displaystyle\frac{D_{s0}}{2\pi Rd_1}(c_0-c_{1,0})+\displaystyle\frac{2D}{l_2}\displaystyle\frac{\partial c_{1,s}}{\partial s}-\displaystyle\frac{D}{hd_1}(c_{1,0}-c_{2,0})$

$\displaystyle\frac{\partial c_{2,0}}{\partial t}=\displaystyle\frac{D}{hd_2}(c_{1,0}-c_{2,0})+\displaystyle\frac{2D}{l_2}\displaystyle\frac{\partial c_{2,s}}{\partial s}-\displaystyle\frac{D_{s2}}{2\pi Rd_2}(c_{2,0}-c_3)$

Como la derivada en el origen es$\displaystyle\frac{\partial}{\partial s}c_{1,s}\Bigr|_{s=0}=-(c_{1,0}-c_1^0)k\tanh(k\pi R)$y$\displaystyle\frac{\partial}{\partial s}c_{2,s}\Bigr|_{s=0}=-(c_{2,0}-c_2^0)k\tanh(k\pi R)$las ecuaciones para la zona del hatch en el caso estatico se reducen a:$\displaystyle\frac{D_{s0}}{2\pi Rd_1}(c_0-c_{1,0})-\displaystyle\frac{2Dk}{l_2}(c_{1,0}-c_1^0)\tanh(k\pi R)-\displaystyle\frac{D}{hd_1}(c_{1,0}-c_{2,0})=0$y$\displaystyle\frac{D}{hd_2}(c_{1,0}-c_{2,0})-\displaystyle\frac{2Dk}{l_2}(c_{2,0}-c_2^0)\tanh(k\pi R)-\displaystyle\frac{D_{s2}}{2\pi Rd_2}(c_{2,0}-c_3)=0$

ID:(8933, 0)

Simulator

Html

ID:(8457, 0)

Modelo 1D

Modelo

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$\displaystyle\frac{d}{dt}c_{1,s}=\displaystyle\frac{1}{2\pi Rd_1}j(j_{s0},c_{s0},c_0,c_{1,s})-j(j_{s1},c_{s1},c_{1,s},c_{2,s}))+\displaystyle\frac{1}{d^2}D(c_{1,s+1}+c_{1,s-1}-2c_{1,s})$

dc_1,s/dt=(1/2piRd_1)(j(j_s0,c_s0,c_0,c_1)--j(j_s1,c_s1,c_1,s,c_2,s))+(1/d^2)D(c_1,s+1+c_1,s-1-2c_1,s)

(ID 8880)

$\displaystyle\frac{d}{dt}c_{2,s}=\displaystyle\frac{1}{2\pi Rd_2}(j(j_{s0},c_{s0},c_{1,s},c_{2,s})-j(j_{s1},c_{s1},c_{2,s},c_3))+\displaystyle\frac{1}{d^2}D(c_{2,s+1}+c_{2,s-1}-2c_{2,s})$

dc_1/dt=(1/2pi Rd_2)(j(j_s0,c_s0,c_1,s,c_2,s)-j(j_s1,c_s1,c_2,s,c_3))+(1/d^2)D(c_2,s+1+c_2.s-1-2c_2,s)

(ID 8881)

$\displaystyle\frac{d}{dt}c_{1,0}=\displaystyle\frac{1}{2\pi Rd_1}j(j_{s0},c_{s0},c_0,c_{1,0})+\displaystyle\frac{2}{dl_2}D(c_{1,1}-c_{1,0})-\displaystyle\frac{1}{hd_1}D(c_{1,0}-c_{2,0})$

dc_1,0/dt=(1/2pi Rd_1)j(j_s0,c_s0,c_0,c_1,0)+(2/dl_2)D(c_1,1-c_1,0)-(1/hd_1)D(c_1,0-c_2,0)

(ID 8882)

$\displaystyle\frac{d}{dt}c_{2,0}=\displaystyle\frac{1}{hd_2}D(c_{1,0}-c_{2,0})+\displaystyle\frac{2}{dl_2}D(c_{2,1}-c_{2,0})-\displaystyle\frac{1}{2\pi Rd_2}j(j_{s2},c_{2s},c_{2,0},c_3)$

d_2l_2dc_2,0/dt=(l_2/h)D(c_1,0-c_2,0)+(2d_2/d)D(c_2,1-c_2,0)-(l_2/2pi R)j(j_s2,c_2s,c_2,0,c_3)

(ID 8883)

$\displaystyle\frac{d}{dt}c_{1,n}=\displaystyle\frac{1}{2\pi Rd_1}(j(j_{s0},c_{s0},c_0,c_{1,n})-j(j_{s1},c_{s1},c_{1,n},c_{2,n}))+\displaystyle\frac{1}{d^2}D(c_{1,n-1}-c_{1,n})$

dc_1,n/dt=(1/2piRd_1)(j(j_s0,c_s0,c_0,c_1)--j(j_s1,c_s1,c_1,n,c_2,n))+(1/d^2)D(c_1,n-1-c_1,n)

(ID 8884)

c_{1,0}=\displaystyle\frac{16D^2\pi^2R^2c_1^0d_1d_2hk^2\tanh(k\pi R)^2+ ((8D^2R^2c_2^0d_2+8D^2R^2c_1^0d_1)kl_2\pi^2+(4DD_{s0}Rc_0d_2+4DD_{s2}Rc_1^0d_1)hkl_2\pi)\tanh(k\pi R)+(2DD_{s2}Rc_3+2DD_{s0}Rc_0)l_2^2\pi+D_{s0}D_{s2}c_0hl_2^2}{16D^2\pi^2R^2d_1d_2hk^2tanh(k\pi R)^2+((8D^2R^2d_2+8D^2R^2d_1)kl_2\pi^2+(4DD_{s0}Rd_2+4DD_{s2}Rd_1)hkl_2\pi)\tanh(k\pi R)+(2DD_{s2}+2DD_{s0})\pi Rl_2^2+D_{s0}D_{s2}hl_2^2}

(ID 8885)

$\displaystyle\frac{\partial c_{1,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_1}(D_{s0}(c_0-c_{1,s})-D_{s1}(c_{1,s}-c_{2,s}))+D\displaystyle\frac{\partial^2c_{1,s}}{\partial s^2}$

\displaystyle\frac{\partial c_{1,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_1}(D_{s0}(c_0-c_{1,s})-D_{s1}(c_{1,s}-c_{2,s}))+D\displaystyle\frac{\partial^2c_{1,s}}{\partial s^2}

(ID 8923)

$\displaystyle\frac{\partial c_{2,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_2}(D_{s0}(c_{1,s}-c_{2,s})-D_{s1}(c_{2,s}-c_3))+D\displaystyle\frac{\partial^2c_{2,s}}{\partial s^2}$

\displaystyle\frac{\partial c_{2,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_2}(D_{s0}(c_{1,s}-c_{2,s})-D_{s1}(c_{2,s}-c_3))+D\displaystyle\frac{\partial^2c_{2,s}}{\partial s^2}

(ID 8924)

\displaystyle\frac{\partial c_{1,0}}{\partial t}=\displaystyle\frac{D_{s0}}{2\pi Rd_1}(c_0-c_{1,0})+\displaystyle\frac{2D}{l_2}\displaystyle\frac{\partial c_{1,s}}{\partial s}-\displaystyle\frac{D}{hd_1}(c_{1,0}-c_{2,0})

(ID 8925)

\displaystyle\frac{\partial c_{2,0}}{\partial t}=\displaystyle\frac{D}{hd_2}(c_{1,0}-c_{2,0})+\displaystyle\frac{2D}{l_2}\displaystyle\frac{\partial c_{2,s}}{\partial s}-\displaystyle\frac{D_{s2}}{2\pi Rd_2}(c_{2,0}-c_3)

(ID 8926)

$c_1^0=\displaystyle\frac{D_{s0}(D_{s0}+D_{s1})}{D_{s1}^2+D_{s0}D_{s1}+D_{s0}^2}c_0+\displaystyle\frac{D_{s1}^2}{D_{s1}^2+D_{s0}D_{s1}+D_{s0}^2}c_3$

c_1^0=D_s0(D_s0+D_s1)c_0/(D_s1^2+D_s0D_s1+D_s0^2)+D_s1^2c_3/(D_s1^2+D_s0D_s1+D_s0^2)

(ID 8927)

$c_2^0=\displaystyle\frac{D_{s1}^2}{D_{s1}^2+D_{s0}D_{s1}+D_{s0}^2}c_0+\displaystyle\frac{D_{s1}(D_{s0}+D_{s1})}{D_{s1}^2+D_{s0}D_{s1}+D_{s0}^2}c_3$

c_2^0=c_0D_s1^2/(D_s1^2+D_s0D_s1+D_s0^2)+c_3D_s1(D_s0+D_s1)/(D_s1^2+D_s0D_s1+D_s0^2)

(ID 8928)

$c_{1,0}=\displaystyle\frac{1+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}{1+\displaystyle\frac{D_{s2}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_0+\displaystyle\frac{\displaystyle\frac{D_{s2}}{D_{s0}}}{1+\displaystyle\frac{D_{2s}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_3$

c_{1,0}=\displaystyle\frac{1+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}{1+\displaystyle\frac{D_{s2}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_0+\displaystyle\frac{\displaystyle\frac{D_{s2}}{D_{s0}}}{1+\displaystyle\frac{D_{2s}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_3

(ID 8929)

$c_{2,0}=\displaystyle\frac{1}{1+\displaystyle\frac{D_{s2}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_0+\displaystyle\frac{\displaystyle\frac{D_{s2}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}{1+\displaystyle\frac{D_{2s}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_3$

c_{2,0}=\displaystyle\frac{1}{1+\displaystyle\frac{D_{s2}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_0+\displaystyle\frac{\displaystyle\frac{D_{s2}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}{1+\displaystyle\frac{D_{2s}}{D_{s0}}+\displaystyle\frac{h}{2\pi R}\displaystyle\frac{D_{s2}}{D}}c_3

(ID 8930)

$k^2=\displaystyle\frac{1}{4\pi R}\left(\displaystyle\frac{(D_{s0}+D_{s1})}{D}\left(\displaystyle\frac{1}{d_1}+\displaystyle\frac{1}{d_2}\right)\pm\sqrt{4\displaystyle\frac{D_{s0}D_{s1}}{D^2d_1d_2}+\displaystyle\frac{(D_{s0}+D_{s1})^2}{D^2}\left(\displaystyle\frac{1}{d_1}-\displaystyle\frac{1}{d_2}\right)^2}\right)$

(ID 8932)

(ID 8934)

Ejemplos

Simplificaci n del Modelo

Lo angosto de la cavidad entre membranas muestra que el sistema se comporta como un sistema de conductores paralelos:

La interacci n entre ambos conductores solo es relevante en procesos muy lentos (minutos) ya que depende de la difusi n perimetral que es muy lenta ($D$).

(ID 8763)

Flujo para $c_1$ en $0 < s < n$

(ID 8890)

Flujo para $c_1$ en $s=0$

(ID 8892)

Flujo para $c_1$ en $s=n$

(ID 8894)

Flujo para $c_2$ en $0 < s < n$

(ID 8891)

Flujo para $c_2$ en $s=0$

(ID 8893)

Flujo para $c_2$ en $s=n$

(ID 8895)

Soluci n Constante

Si se asumen $c_0$ y $c_3$ constantes tanto en el tiempo como en el per metro se tiene que las ecuaciones

$\displaystyle\frac{d}{dt}c_{1,0}=\displaystyle\frac{1}{2\pi Rd_1}j(j_{s0},c_{s0},c_0,c_{1,0})+\displaystyle\frac{2}{dl_2}D(c_{1,1}-c_{1,0})-\displaystyle\frac{1}{hd_1}D(c_{1,0}-c_{2,0})$

$\displaystyle\frac{d}{dt}c_{1,s}=\displaystyle\frac{1}{2\pi Rd_1}j(j_{s0},c_{s0},c_0,c_{1,s})-j(j_{s1},c_{s1},c_{1,s},c_{2,s}))+\displaystyle\frac{1}{d^2}D(c_{1,s+1}+c_{1,s-1}-2c_{1,s})$

implican que las soluciones para $c_{1,s}$ y $c_{2,s}$ se pueden escribir como una constante mas una parte que puede depender de la posici n y/o del tiempo:$c_{1,s}=c_1^0+c_1(s,t)$y$c_{2,s}=c_2^0+c_2(s,t)$Introduciendo ambas soluciones en las ecuaciones anteriores se tiene que se pueden elegir $c_1^0$ y $c_2^0$ de modo que $c_1(s,t)$ y $c_2(s,t)$ ya no dependen de $c_0$ y $c_3$. Esto se da si$D_{s0}(c_0-c_1^0)-D_{s1}(c_1^0-c_2^0)=0$y$D_{s0}(c_1^0-c_2^0)-D_{s1}(c_2^0-c_3)=0$

(ID 8896)

Dependencia Espacial

Para el caso estacionario las ecuaciones de la parte de la soluci n que dependen del per metro se obtienen de

$\displaystyle\frac{\partial c_{1,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_1}(D_{s0}(c_0-c_{1,s})-D_{s1}(c_{1,s}-c_{2,s}))+D\displaystyle\frac{\partial^2c_{1,s}}{\partial s^2}$

$\displaystyle\frac{\partial c_{2,s}}{\partial t}=\displaystyle\frac{1}{2\pi Rd_2}(D_{s0}(c_{1,s}-c_{2,s})-D_{s1}(c_{2,s}-c_3))+D\displaystyle\frac{\partial^2c_{2,s}}{\partial s^2}$

siendo$\displaystyle\frac{d^2}{ds^2}c_{1,s}=\displaystyle\frac{1}{2\pi Rd_1}\displaystyle\frac{(D_{s0}+D_{s1})}{D}c_{1,s}-\displaystyle\frac{1}{2\pi Rd_1}\displaystyle\frac{D_{s1}}{D}c_{2,s}$y$\displaystyle\frac{d^2}{ds^2}c_{2,s}=\displaystyle\frac{1}{2\pi Rd_2}\displaystyle\frac{(D_{s0}+D_{s1})}{D}c_{2,s}-\displaystyle\frac{1}{2\pi Rd_2}\displaystyle\frac{D_{s0}}{D}c_{1,s}$La soluci n tiene la forma$c_{1,s}=A_1e^{ks}$y$c_{2,s}=A_2e^{ks}$Si se introduce esta soluci n en la ecuaci n se obtiene que $k$ debe satisfacer:$(D_{s0}+D_{s1}-2\pi Rd_1Dk^2)(D_{s0}+D_{s1}-2\pi Rd_2Dk^2)=D_{s0}D_{s1}$

(ID 8931)

Soluci n Perimetral

Como el vector de onda es positivo la soluci n es una suma de exponenciales $e^{ks}$ y $e^{-ks}$. Por otro lado, como debe ser simetrica respecto del origen en $s=0$ y continua en el otro extremo $s=\pi R$ se debe tener que la pendiente en dicho punto debe ser nula. Por ello la soluci n debe corresponder a un coseno hiperbolico. Si se considera el factor constante antes calculado ser de la forma

$c_1(s)=c_1^0+(c_{1,0}-c_1^0)\displaystyle\frac{\cosh k(\pi R - s)}{\cosh k\pi R}$

y

$c_2(s)=c_2^0+(c_{2,0}-c_2^0)\displaystyle\frac{\cosh k(\pi R - s)}{\cosh k\pi R}$

donde $c_{1,0}$ y $c_{2,0}$ son las concentraciones frente al hatch. Para calcular ambas concentraciones basta con reemplazar las funciones en

(ID 8933)

Simulator

(ID 8457)

ID:(1037, 0)