Storyboard

Science allows us to describe situations and the evolution of systems in the real world. It is based on variables that can be measured and on equations that relate them, enabling their calculation and, therefore, prediction.

Each variable can be compared to a brick piece that is assembled to form equations, functioning as a functional element. These different equations allow us to build a model, similar to a brick toy that can be used in various ways.

The different ways of using it correspond to the possible calculations that can be made with various data sets and the necessary intermediate steps.

The use of this model is what we call in physics problem solving.

>Model

ID:(1931, 0)

Concept

>Top

We can establish an analogy between a real-life situation and a brick toy.

The analogy between reality in the form of a journey and a brick toy

In the real-life situation, variables are defined and equations are formulated that link them together.

In the case of the toy, bricks and pieces are used and assembled to build the model.

Each brick, in this way, represents a variable that connects different parts, similar to how equations do.

ID:(14372, 0)

Concept

>Top

If the modeling of a traveling vehicle is considered, the initial position $s_0$ and the final reached position $s$ must be entered:

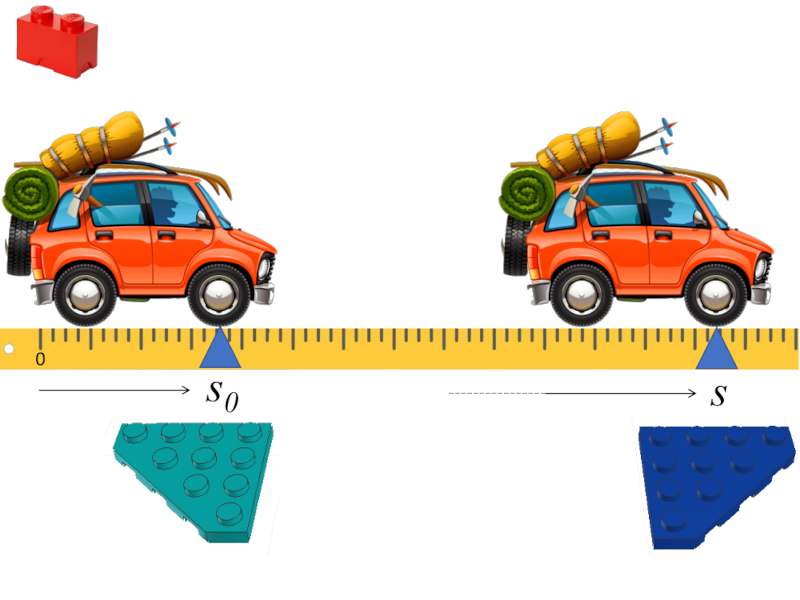
The analogy between variables and bricks

Within the analogy, a brick is associated with each variable. As they are different variables, they are differentiated in this case by their color.

ID:(14373, 0)

Concept

>Top

Within the model it makes sense to calculate the path traveled $\Delta s$.

To do this, a new brick must be introduced into the analogy.

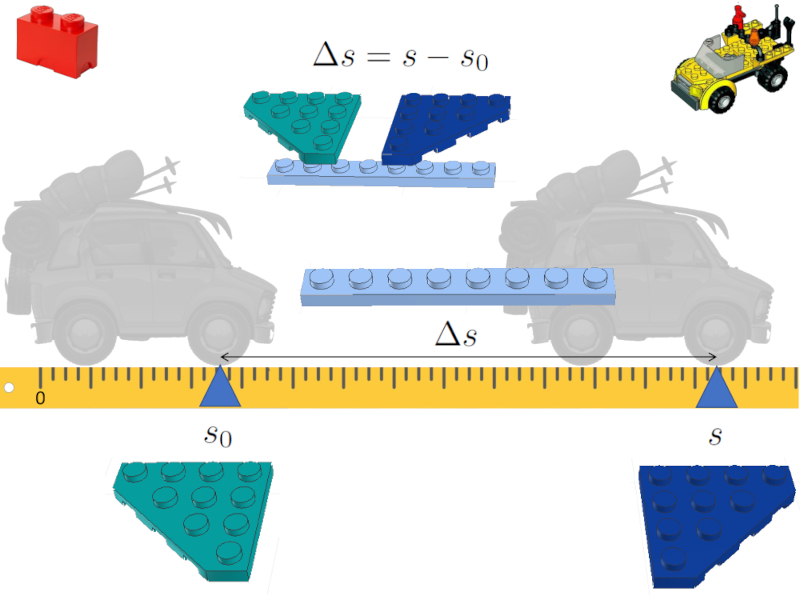
The analogy between equations and sets of bricks

For its calculation, the corresponding equation must be defined, which in this case corresponds to

$\Delta s = s - s_0$

In our analogy, bricks are connected to form the first unit of our model.

ID:(14374, 0)

Concept

>Top

To describe motion in our model, it is necessary to introduce time.

Analogous to position, one must consider an initial time $t_0$, a final time $t$, and the elapsed time $\Delta t$.

Each of these variables is represented as a brick in the image:

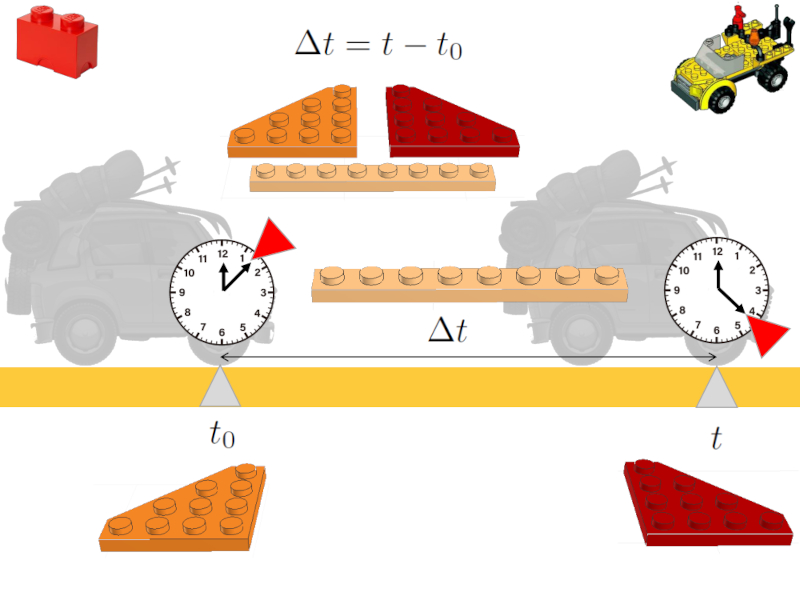
The introduction of time and the brick analogy

Additionally, the elapsed time is introduced, defined by an equation of the form:

$\Delta t = t - t_0$

This equation is represented in the analogy as a new unit within the brick model.

ID:(14375, 0)

Concept

>Top

To predict how the vehicle will move, you must enter the speed.

This is defined as the ratio of the distance covered and the time elapsed.

Within the analogy, the bricks of the path traveled are taken with that of the time elapsed and they are mounted on a new brick that represents the speed:

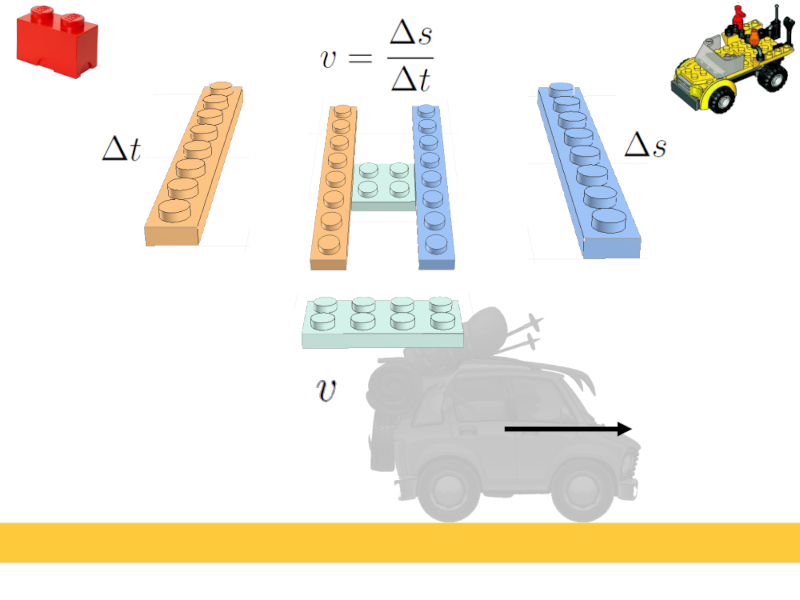
The analogy for the introduction of speed

Thus, the third equation is introduced

$v = \displaystylefrac{\Delta s}{\Delta t}$

ID:(14376, 0)

Concept

>Top

If the brick model is fully assembled, additional relationships are obtained that correspond to other descriptions of groups of bricks.

In this way, the model is represented by the five variables already defined and by a total of four equations:

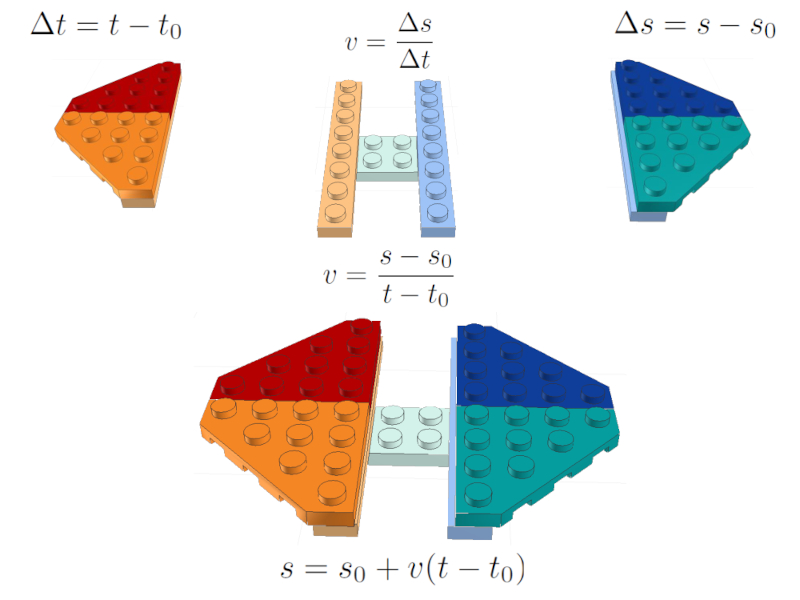
Set of all equations

In the central part, the additional equation that arises from assembling the complete model is shown.

ID:(14377, 0)

Top

>Top

Finally, the complete model is obtained, that is, the variables and the equations that relate them.

In the analogy, it is practically a kind of instruction manual for a brick model, where the necessary bricks and the elements being built are listed.

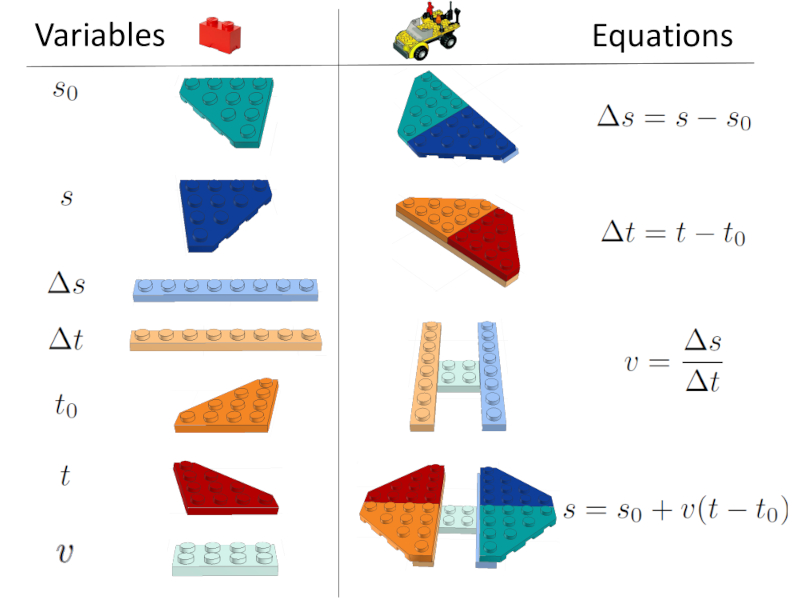
Instructions of the model in the LEGO style

ID:(14378, 0)