Usuario:


Pronostico de periodo
Storyboard

Una vez se ha determinado el segmento similar se puede obtener los datos que lo siguen.

Con la forma como varia la magnitud se puede se puede estimar como debiese continuar el parámetro climático después del segmento actual.

Si se realiza el análisis con un segmento de referencia del pasado reciente, en que existen datos posteriores reales, se pueden comparar estos con el pronostico.

De esta forma se puede estimar el error del pronostico.

>Modelo

ID:(1914, 0)


Gráfica del pronóstico
Definición

Si se grafica la función calculada en los 36 meses posteriores al tiempo en que se calcularon los modos se obtiene un pronostico para el parametro:

ID:(14358, 0)


Error de pronóstico
Imagen

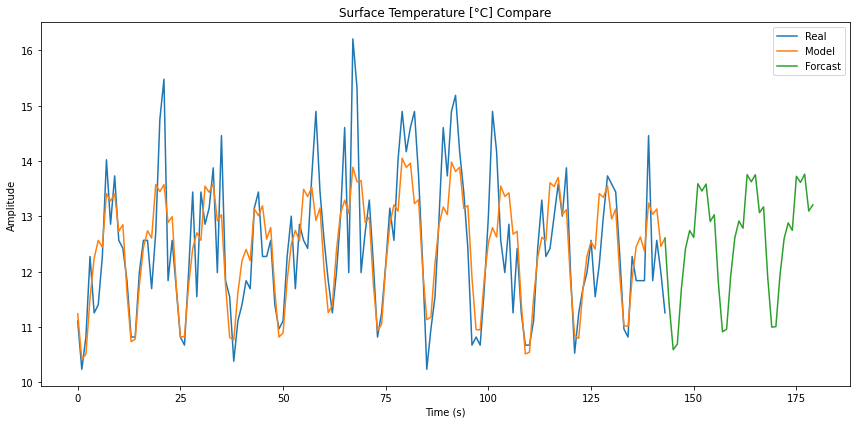
Si se reserva el ultimo año para evaluar el error y se calculan los modos con las 12 años anteriores. Con dichos modos se puede realizar un pronostico para los 12 meses que se reservaron y compararlo con los datos reales. De esta forma se puede estimar la calidad del pronostico para datos ya ocurridos que no se empelaron para el proceso de modelar.

ID:(14360, 0)


Pronostico de periodo
Descripción

Una vez se ha determinado el segmento similar se puede obtener los datos que lo siguen.\n\nCon la forma como varia la magnitud se puede se puede estimar como debiese continuar el parámetro climático después del segmento actual.\n\nSi se realiza el análisis con un segmento de referencia del pasado reciente, en que existen datos posteriores reales, se pueden comparar estos con el pronostico.\n\nDe esta forma se puede estimar el error del pronostico.\n

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

La transformada de Fourier

$ x(t) = \displaystyle\sum_{k=-\infty}^{\infty}( a_k \cos 2 \pi \nu_k t + b_k \sin 2 \pi \nu_k t )$



se puede con la relaci n de Euler

$ e^{i \theta } = \cos \theta + i\sin \theta $



la definici n

$ X_k = a_k - i b_k $



y la descreticaci n del tiempo

$ t_n = n \Delta t $



redefinir como las trasformada discreta en el espacio complejo de la serie temporal x_n igual a

$ x_n = \displaystyle\sum_{k=0}^{N-1} X_k e^{ i 2 \pi \nu_k n \Delta t }$

(ID 14351)

Si se grafica la funci n calculada en los 36 meses posteriores al tiempo en que se calcularon los modos se obtiene un pronostico para el parametro:

(ID 14358)

La eliminaci n de las fluctuaciones conlleva a un error inherente al m todo. Para estimarlo se puede directamente comparar el valor real con el estimado sin la fluctuaci n. Para ello se puede obtener el promedio de la diferencia dividido por el valor medio:

$\epsilon = 2 \displaystyle\sum_n\displaystyle\frac{\mid x_n - \bar{x}_n\mid}{\mid x_n + \bar{x}_n\mid}$



Esto se puede calcular con el c digo

cnt0 = 0
err0 = 0
for i in range(len(x)):
    if Xm[i] + x[i] != 0:
        err0 = err0 + 2*abs(Xm[i] - x[i])/(Xm[i] + x[i])
        cnt0 = cnt0 + 1
        
err0 = err0/cnt0

donde x es el valor real y Xm aquel en que no se incluye la fluctuaci n.

(ID 14359)

Si se reserva el ultimo a o para evaluar el error y se calculan los modos con las 12 a os anteriores. Con dichos modos se puede realizar un pronostico para los 12 meses que se reservaron y compararlo con los datos reales. De esta forma se puede estimar la calidad del pronostico para datos ya ocurridos que no se empelaron para el proceso de modelar.

(ID 14360)

ID:(1914, 0)