User:
Heat transfer
Storyboard 
Heat is conducted within a medium up to the interface with another medium. Between the two, heat is transferred based on the temperature difference between the media, the contact surface, and a thermal transfer constant. When one of the media is a gas (e.g., air) or a liquid (e.g., water), the thermal transfer constant depends on the structure of the interface and the flow rate of the gaseous or liquid medium.
ID:(776, 0)
Dependence of heat transfer on geometry to the conductor
Image
The primary driver of heat transfer from a medium to a conductor is the difference in temperature. In the medium the indoor temperature ($T_i$), particles have more energy, and when they collide with those in the conductor at ERROR:5212.1, they tend to increase the energy of the latter. This interaction can be represented as follows:
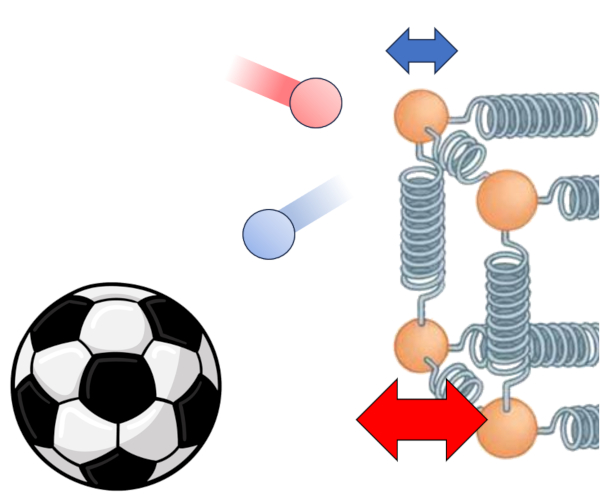
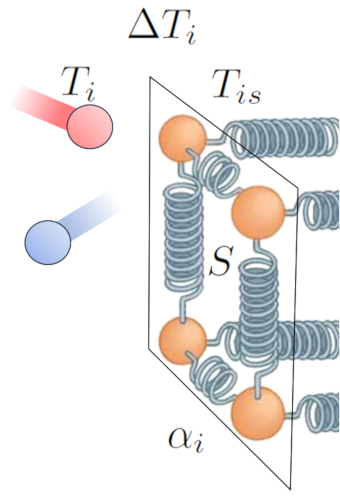
Beyond temperature itself, the heat flow depends on the temperature difference at internal interface ($\Delta T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
Another key factor is the number of atoms whose oscillation amplitude can be increased, which depends on the section ($S$). Lastly, we must consider surface properties, described by the internal transmission coefficient ($\alpha_i$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
ID:(15237, 0)
Calculation of heat transmission to the conductor
Note
In this way, we establish a relationship that allows us to calculate the heat flow rate ($q$) based on the temperature difference at internal interface ($\Delta T_i$), and the internal transmission coefficient ($\alpha_i$):
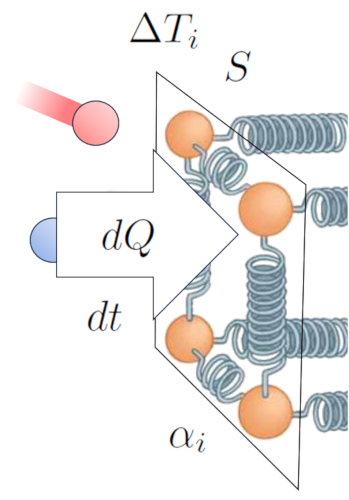
This can be expressed mathematically as follows:
| $ q = \alpha_i \Delta T_i $ |
ID:(15238, 0)
Dependence of heat transfer on geometry from the conductor
Quote
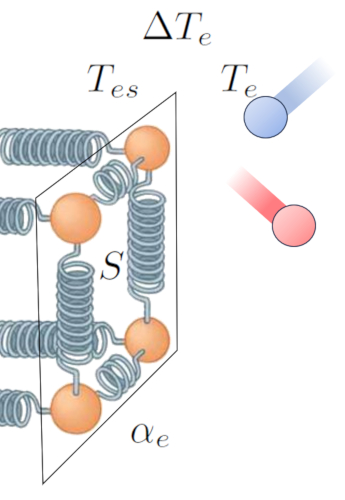
The primary driver of heat transfer from a conductor to a medium is the temperature difference. When the outer surface temperature ($T_{es}$), particles have more energy and oscillate with a greater amplitude when interacting with the atoms and molecules of the medium at ERROR:5207.1. This tends to increase the energy of the latter. This interaction can be represented as follows:
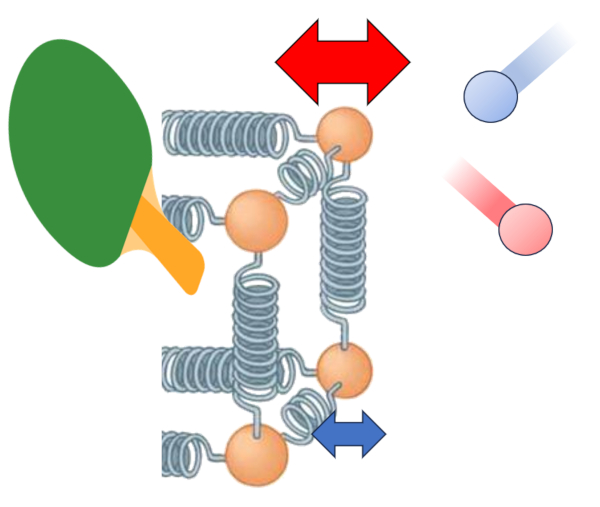
Beyond temperature, the heat flow depends on the temperature difference at external interface ($\Delta T_e$).
| $ \Delta T_e = T_{es} - T_e $ |
Another key factor is the number of atoms that can have their oscillation amplitude increased, which depends on the section ($S$). Finally, we must consider surface properties, represented by the external transmission coefficient ($\alpha_e$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
ID:(15239, 0)
Heat transfer from the conductor
Exercise
In this manner, we establish a relationship that enables us to calculate the heat flow rate ($q$) based on the temperature difference at external interface ($\Delta T_e$), and the external transmission coefficient ($\alpha_e$):
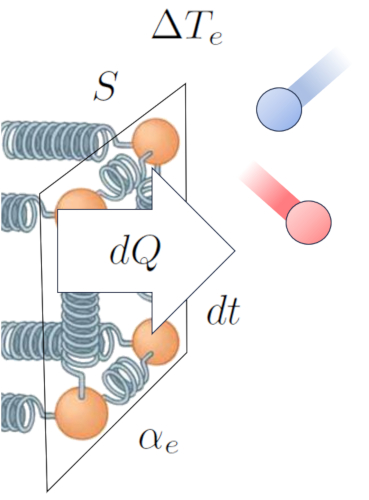
This can be expressed mathematically as follows:
| $ q = \alpha_e \Delta T_e $ |
ID:(15240, 0)
Heat transfer to and from the conductor
Equation
The first description of the heat transfer model at the interface between two media was developed by Thomas Graham Balfour [1]. His theory posits that the rate of heat transfer depends on the temperature difference and a specific constant of the interface.
When heat is transferred to the conductor, represented by the heat flow rate ($q$) along with the internal transmission coefficient ($\alpha_i$) and the temperature difference at internal interface ($\Delta T_i$), the relationship is expressed by the following equation:
| $ q = \alpha_i \Delta T_i $ |
In the case where heat passes from the conductor, identified by the heat flow rate ($q$) with the external transmission coefficient ($\alpha_e$) and the temperature difference at external interface ($\Delta T_e$), the relationship is specified as:
| $ q = \alpha_e \Delta T_e $ |
[1] "The Theory of Heat", Thomas Graham Balfour, 1876.
ID:(15123, 0)
Heat transport
Script
The basic system includes a transfer generated by the temperature difference ($\Delta T$), which consists of the temperature difference at internal interface ($\Delta T_i$), the temperature difference in the conductor ($\Delta T_0$), and the temperature difference at external interface ($\Delta T_e$). Therefore:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
With the heat flow rate ($q$) being responsible for the transfer between the interior and the conductor, using the internal transmission coefficient ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
Conduction involves the thermal conductivity ($\lambda$) and the conductor length ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
And the transfer from the conductor to the exterior, with the external transmission coefficient ($\alpha_e$), is represented by:
| $ q = \alpha_e \Delta T_e $ |
All this is graphically represented by:
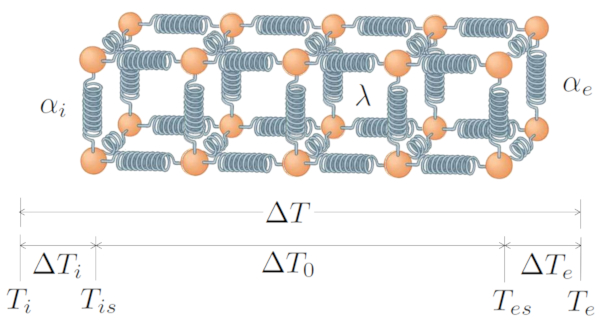
ID:(7723, 0)
Dependence of the transfer coefficient on the velocity of the medium
Variable
One of the effects of heat transfer from a conductor to an external medium is the heating of the medium near the interface, creating an interference zone in the transmission. This decreases the efficiency of the transfer and tends to form an insulating layer that reduces the flow of energy.
However, this effect can change in the presence of wind. The wind can remove the layer of high-temperature atoms and molecules, enhancing the efficiency of heat transfer. This suggests that the transmission coefficient ($\alpha$) is influenced by the mean speed ($v_m$) [1,2]:
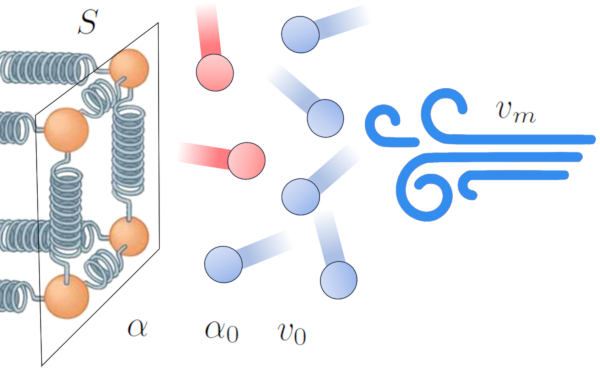
In this context, we model the relationship based on ERROR:9844,0 and a reference factor of the media reference speed ($v_0$).
The mathematical relationship that describes this phenomenon for a gas with the transmission coefficient in gases, dependent on speed ($\alpha_{gv}$), the mean speed ($v_m$), the transmission coefficient in gases, independent of speed ($\alpha_{g0}$), and the transmission coefficient gas velocity factor ($v_{g0}$) is:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
And for a liquid with the transmission coefficient dependent on the speed ($\alpha_{wv}$), the mean speed ($v_m$), the transmission coefficient Independent of the speed ($\alpha_{w0}$), and the factor velocidad del coefiente de transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
This illustrates how wind can significantly influence the efficiency of heat transfer between a conductor and an external medium.
[1] "Über Flüssigkeitsbewegung bei sehr kleiner Reibung" (On Fluid Movement with Very Little Friction), Ludwig Prandtl, 1904
[2] "Die Abhängigkeit der Wärmeübergangszahl von der Rohrlänge" (The Dependence of the Heat Transfer Coefficient on the Length of the Pipe), Wilhelm Nusselt, 1910
ID:(3620, 0)
Heat transfer
Storyboard
Heat is conducted within a medium up to the interface with another medium. Between the two, heat is transferred based on the temperature difference between the media, the contact surface, and a thermal transfer constant. When one of the media is a gas (e.g., air) or a liquid (e.g., water), the thermal transfer constant depends on the structure of the interface and the flow rate of the gaseous or liquid medium.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
Consider a volume where particles bounce off the walls at a speed representing their temperature. Each time they strike a central grid, they collide with the atoms of a solid, causing them to start oscillating. This oscillation propagates through the solid until it reaches the opposite end, where energy is transferred to the gas through new collisions.
Experimentation:
You can adjust the speed of the particles in the side boxes and observe how energy is transferred into the solid and then to the gas on the opposite side.
The primary driver of heat transfer from a medium to a conductor is the difference in temperature. In the medium the indoor temperature ($T_i$), particles have more energy, and when they collide with those in the conductor at ERROR:5212.1, they tend to increase the energy of the latter. This interaction can be represented as follows:
Beyond temperature itself, the heat flow depends on the temperature difference at internal interface ($\Delta T_i$):
Another key factor is the number of atoms whose oscillation amplitude can be increased, which depends on the section ($S$). Lastly, we must consider surface properties, described by the internal transmission coefficient ($\alpha_i$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
In this way, we establish a relationship that allows us to calculate the heat flow rate ($q$) based on the temperature difference at internal interface ($\Delta T_i$), and the internal transmission coefficient ($\alpha_i$):
This can be expressed mathematically as follows:
The primary driver of heat transfer from a conductor to a medium is the temperature difference. When the outer surface temperature ($T_{es}$), particles have more energy and oscillate with a greater amplitude when interacting with the atoms and molecules of the medium at ERROR:5207.1. This tends to increase the energy of the latter. This interaction can be represented as follows:
Beyond temperature, the heat flow depends on the temperature difference at external interface ($\Delta T_e$).
Another key factor is the number of atoms that can have their oscillation amplitude increased, which depends on the section ($S$). Finally, we must consider surface properties, represented by the external transmission coefficient ($\alpha_e$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
In this manner, we establish a relationship that enables us to calculate the heat flow rate ($q$) based on the temperature difference at external interface ($\Delta T_e$), and the external transmission coefficient ($\alpha_e$):
This can be expressed mathematically as follows:
The first description of the heat transfer model at the interface between two media was developed by Thomas Graham Balfour [1]. His theory posits that the rate of heat transfer depends on the temperature difference and a specific constant of the interface.
When heat is transferred to the conductor, represented by the heat flow rate ($q$) along with the internal transmission coefficient ($\alpha_i$) and the temperature difference at internal interface ($\Delta T_i$), the relationship is expressed by the following equation:
In the case where heat passes from the conductor, identified by the heat flow rate ($q$) with the external transmission coefficient ($\alpha_e$) and the temperature difference at external interface ($\Delta T_e$), the relationship is specified as:
[1] "The Theory of Heat", Thomas Graham Balfour, 1876.
The basic system includes a transfer generated by the temperature difference ($\Delta T$), which consists of the temperature difference at internal interface ($\Delta T_i$), the temperature difference in the conductor ($\Delta T_0$), and the temperature difference at external interface ($\Delta T_e$). Therefore:
With the heat flow rate ($q$) being responsible for the transfer between the interior and the conductor, using the internal transmission coefficient ($\alpha_i$):
Conduction involves the thermal conductivity ($\lambda$) and the conductor length ($L$):
And the transfer from the conductor to the exterior, with the external transmission coefficient ($\alpha_e$), is represented by:
All this is graphically represented by:
One of the effects of heat transfer from a conductor to an external medium is the heating of the medium near the interface, creating an interference zone in the transmission. This decreases the efficiency of the transfer and tends to form an insulating layer that reduces the flow of energy.
However, this effect can change in the presence of wind. The wind can remove the layer of high-temperature atoms and molecules, enhancing the efficiency of heat transfer. This suggests that the transmission coefficient ($\alpha$) is influenced by the mean speed ($v_m$) [1,2]:
In this context, we model the relationship based on ERROR:9844,0 and a reference factor of the media reference speed ($v_0$).
The mathematical relationship that describes this phenomenon for a gas with the transmission coefficient in gases, dependent on speed ($\alpha_{gv}$), the mean speed ($v_m$), the transmission coefficient in gases, independent of speed ($\alpha_{g0}$), and the transmission coefficient gas velocity factor ($v_{g0}$) is:
And for a liquid with the transmission coefficient dependent on the speed ($\alpha_{wv}$), the mean speed ($v_m$), the transmission coefficient Independent of the speed ($\alpha_{w0}$), and the factor velocidad del coefiente de transmisión ($v_{w0}$):
This illustrates how wind can significantly influence the efficiency of heat transfer between a conductor and an external medium.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (On Fluid Movement with Very Little Friction), Ludwig Prandtl, 1904
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (The Dependence of the Heat Transfer Coefficient on the Length of the Pipe), Wilhelm Nusselt, 1910
The temperature difference at internal interface ($\Delta T_i$) is calculated by subtracting the inner surface temperature ($T_{is}$) from the indoor temperature ($T_i$):
The temperature difference at external interface ($\Delta T_e$) is calculated by subtracting the outer surface temperature ($T_{es}$) from the outdoor temperature ($T_e$):
In the case of a solid, and similarly for a liquid, we can describe the system as a structure of atoms held together by something that behaves like a spring. When both ends have temperatures of ERROR:10165.1, with the inner surface temperature ($T_{is}$) and the outer surface temperature ($T_{es}$):
In the process of heat transfer, the temperature gradually decreases from the system with the highest temperature (internal) to the one with the lowest temperature (external). In this process, it first decreases from the internal average temperature to the temperature difference at internal interface ($\Delta T_i$), then to the temperature difference in the conductor ($\Delta T_0$), and finally to the temperature difference at external interface ($\Delta T_e$). The sum of these three variations equals the total drop, that is, the temperature difference ($\Delta T$), as shown below:
The the heat flow rate ($q$) is defined based on the heat transported ($dQ$) passing through the section ($S$) in the time variation ($dt$):
In this way, we establish a relationship that allows us to calculate the heat flow rate ($q$) based on the temperature difference at internal interface ($\Delta T_i$), and the internal transmission coefficient ($\alpha_i$):
In this manner, we establish a relationship that enables us to calculate the heat flow rate ($q$) based on the temperature difference at external interface ($\Delta T_e$), and the external transmission coefficient ($\alpha_e$):
The heat flux ($q$) is a function of the thermal conductivity ($\lambda$), the conductor length ($L$) and the temperature difference in the conductor ($\Delta T_0$):
If a medium is moving with a constant of the transmission coefficient dependent on the speed ($\alpha_{wv}$), and the mean speed ($v_m$) is equal to
where the transmission coefficient Independent of the speed ($\alpha_{w0}$) represents the case where the medium is not moving, and the factor velocidad del coefiente de transmisión ($v_{w0}$) is the reference velocity.
The thermal transfer constant of the material for the case of a stationary liquid is equal to $340 J/m^2sK$, while the reference velocity is $0.0278 m/s$.
In the event that a medium moves with a constant value of ERROR:5250.1 and the transmission coefficient in gases, dependent on speed ($\alpha_{gv}$) is equal to
where the transmission coefficient in gases, independent of speed ($\alpha_{g0}$) represents the scenario where the medium does not move, and the transmission coefficient gas velocity factor ($v_{g0}$) is the reference velocity.
The thermal transfer constant for the material in the case of a stationary gas is equal to $5.6 J/m^2sK$, while the reference velocity is $1.41 m/s$.
ID:(776, 0)