Usuario:
Formación de Gotas
Storyboard
A medida que un vapor de un liquido comienza a condensar las moléculas pasan al estado liquido con lo que no tienen la energía de evitar ligadas a otras moléculas o ser absorbidas por gotas que se hayan ido formando. La velocidad con que crecen estas gotas depende de la concentración de vapor de agua y el tamaño de estas.
ID:(1333, 0)
Trabajo realizado
Ecuación
El trabajo aportado o realizado ($W$) es igual a la integral de la presión ($p$) en el volumen ($V$) desde $V_1$ hasta $V_2$. Esto representa el trabajo realizado por la máquina, que se puede expresar como:
 $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
ID:(10253, 0)
Representación gráfica del trabajo obtenido
Imagen
Dado que el trabajo es
| $ \delta W = p dV $ |
se puede representar en un gráfico de presión versus volumen como el área debajo de la curva de presión en función del volumen:
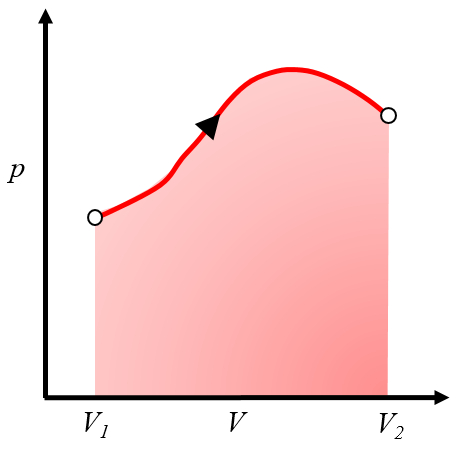
Este área representa el trabajo obtenido cuando un gas realiza trabajo al expandirse desde el volumen $V_1$ al volumen $V_2$.
Normalmente, este proceso se logra calentando el sistema, lo que provoca la expansión y realiza el trabajo. Un ejemplo sería un pistón con gas calentado en una caldera.
ID:(10266, 0)
Representación gráfica del trabajo a ser invertido
Imagen
Para repetir el proceso, es necesario volver del volumen $V_2$ al volumen $V_1$, lo que implica seguir una curva en el diagrama de presión versus volumen en sentido contrario:
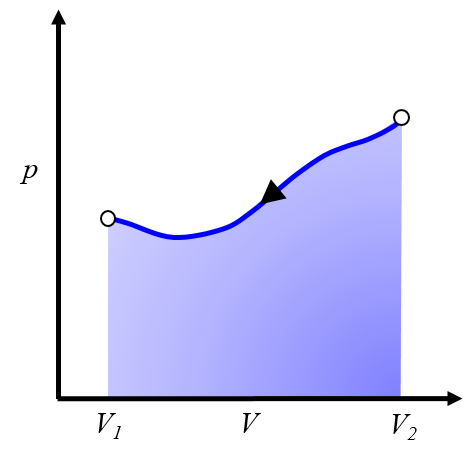
Esto representa un trabajo que debe ser invertido y que debemos suministrar para poder repetir el ciclo.
Por lo general, este proceso se logra enfriando el sistema, lo que provoca su contracción. La energía que debemos invertir corresponde al calor retirado del sistema.
ID:(10254, 0)
Trabajo a invertir
Ecuación
Al contraer el volumen desde $V_2$ a $V_1$, es necesario suministrar energía a la máquina, representada por
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
La necesidad de suministrar esta energía se refleja en el signo del integral.
ID:(10255, 0)
Representación gráfica del trabajo efectivo obtenido
Imagen
El trabajo neto obtenido es la diferencia entre el trabajo obtenido y el trabajo necesario para completar el ciclo:
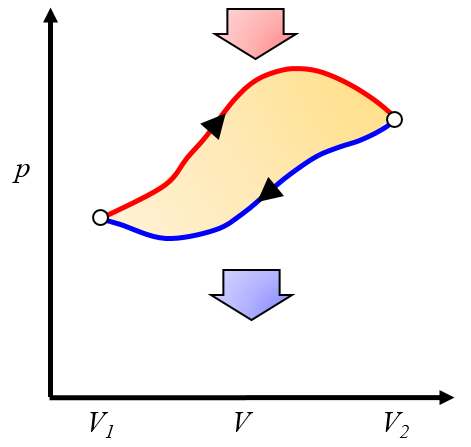
ID:(10268, 0)
Trabajo total
Ecuación
El trabajo total se calcula integrando sobre el ciclo completo, es decir, la parte en la que se realiza trabajo
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
y la parte en la que se invierte el proceso
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
que se convierte en una resta. Este proceso cíclico se representa matemáticamente mediante una integral con un círculo y corresponde a la suma de los elementos debajo de la curva en cada etapa:
| $\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$ |
ID:(10256, 0)
Modelo simplificado
Imagen
Una manera sencilla de modelar una máquina termodinámica es asumir que trabaja de manera isotérmica y adiabática.
| $W=\displaystyle\oint_C T\,dS$ |
Esto se puede representar en el espacio temperatura versus entropía, en el que se observan dos segmentos isotérmicos y dos adiabáticos:
ID:(10257, 0)
Máquina termodinámica y primera ley
Ecuación
Dado que el trabajo generado por la máquina termodinámica es igual a
| $\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$ |
y la primera ley de la termodinámica es
| $ dU = \delta Q - p dV $ |
se deduce que
$\displaystyle\oint_C p dV=\displaystyle\oint_C (\delta Q -dU)$
Por lo tanto, el trabajo es igual a
| $\delta W=\displaystyle\oint_C (\delta Q -dU)$ |
ID:(10258, 0)
Maquina termodinámica y segunda ley
Ecuación
Dado que el trabajo es igual a
| $\delta W=\displaystyle\oint_C (\delta Q -dU)$ |
se puede deducir, de acuerdo con la segunda ley de la termodinámica
| $ \delta Q = T dS $ |
que esto se puede expresar como
| $\delta W=\displaystyle\oint_C (TdS -dU)$ |
ID:(10259, 0)
Caso adiabático
Ecuación
En las fases en las que el proceso es adiabático, la energía interna no varía
| $ dU =0$ |
por lo que el trabajo realizado por la máquina termodinámica
| $\delta W=\displaystyle\oint_C (TdS -dU)$ |
se reduce a
| $W=\displaystyle\oint_C T\,dS$ |
ID:(10260, 0)
Trabajo en el modelo simplificado
Ecuación
La integral en el modelo simplificado,
| $W=\displaystyle\oint_C T\,dS$ |
puede estimarse de manera sencilla utilizando la fórmula de área, multiplicando la altura por la base del área que representa el trabajo:
| $ W =( T_H - T_C )( S_H - S_L )$ |
ID:(10261, 0)
Calor aportado
Ecuación
The heat supplied to expand the gas is calculated directly by integrating the entropy from
| $W=\displaystyle\oint_C T\,dS$ |
from $S_L$ to $S_H$.
| $Q_H=T_H(S_H-S_L)$ |
ID:(10262, 0)
Calor a retirar (refrigerar)
Ecuación
El calor necesario para restaurar el sistema se calcula directamente mediante la integración de la entropía en
| $W=\displaystyle\oint_C T\,dS$ |
desde $S_H$ hasta $S_L$.
| $Q_C=T_C(S_H-S_L)$ |
ID:(10263, 0)
Rendimiento
Ecuación
El rendimiento de la máquina se define como la relación entre el trabajo obtenido y la energía total suministrada, lo que representa una medida de cuánto se puede aprovechar en relación con lo que se aporta.
| $\eta=\displaystyle\frac{W}{Q_H}$ |
ID:(10264, 0)
Rendimiento de Carnot
Ecuación
Si definimos el rendimiento como
| $\eta=\displaystyle\frac{W}{Q_H}$ |
y utilizamos la expresión para el trabajo
| $ W =( T_H - T_C )( S_H - S_L )$ |
y el calor aportado
| $Q_H=T_H(S_H-S_L)$ |
obtenemos la relación del rendimiento en función de la temperatura, conocida como el rendimiento de Carnot.
| $\eta=1-\displaystyle\frac{T_C}{T_H}$ |
Es esencial recordar que estamos hablando de temperatura absoluta y que, según la segunda ley de la termodinámica, el rendimiento siempre será menor que uno. En otras palabras, siempre habrá una pérdida de calor que representa energía no aprovechada.
ID:(10265, 0)
Modelo más complejo
Imagen
Un modelo más realista se puede desarrollar utilizando un gas ideal, en el que:
Se expande desde un volumen $V_1$ a $V_2$ de manera isotérmica a una temperatura $T_H$.
Luego, continúa expandiéndose desde un volumen $V_2$ a un volumen $V_3$ de manera adiabática, enfriándose desde la temperatura $T_H$ a $T_C$.
Después, se contrae de manera isotérmica desde el volumen $V_3$ hasta el volumen $V_4$ mientras mantiene una temperatura de $T_C$.
Finalmente, continúa contrayéndose desde el volumen $V_4$ hasta el volumen $V_1$ de manera adiabática mientras se calienta de la temperatura $T_C$ a $T_H$.
Esto se resume en la siguiente gráfica:
El proceso realiza trabajo en el punto 1 a través de la ruta 2 a 3, mientras que se debe realizar trabajo desde el punto 3 a través de la ruta 4 a 1. Esto se logra suministrando calor en la primera etapa y extrayendo calor en la segunda.
ID:(10267, 0)