Druyd:Knowledge

Límites de Estadiísticas de Gases Cuanticos

Storyboard

>Modell

ID:(514, 0)

Ocupación de estados

Definition

ID:(13508, 0)

Potencial químico en las tres distribuciones

Bild

ID:(13509, 0)

Límites de Estadiísticas de Gases Cuanticos

Beschreibung

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$\alpha$

alpha

Alpha

$\beta$

beta

Beta

1/J

$\epsilon_r$

epsilon_r

Energía de la partícula en el estado

$r$

$\epsilon_r$

epsilon_r

Energía del fermion en el estado

$r$

$\alpha$

alpha

Factor alpha

$\beta$

beta

Factor beta

1/J

$Z_{BE/FD}$

Z_BEFD

Función partición de Bose-Einstein/Fermi-Dirac

$Z_{MB}$

Z_MB

Función partición de Maxwell-Boltzmann

$N$

Numero de partículas

$n_r$

n_r

Numero de partículas en el estado

$r$

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$N =\displaystyle\sum_ r \displaystyle\frac{1}{e^{ \alpha + \beta \epsilon_r }\pm 1}$

N =sum_r 1/(e^( alpha + beta * epsilon_r )+/-1)

(ID 3731)

$n_r=\displaystyle\frac{1}{e^{\alpha+\beta\epsilon_r}\pm 1}$

n_r=\displaystyle\frac{1}{e^{\alpha+\beta\epsilon_r}\pm 1}

(ID 3732)

$\ln Z_{BE/FD} = \alpha N \pm\displaystyle\sum_ r \ln(1\pm e^{- \alpha - \beta \epsilon_r })$

ln Z_BE/FD = alpha * N +/- sum_rln(1 +/- exp( -alpha - beta* epsilon_r ))

(ID 3733)

$n_r=e^{-\alpha-\beta\epsilon_r}$

n_r=e^{-\alpha-\beta\epsilon_r}

(ID 3734)

$\alpha =- \ln N +\ln\left(\displaystyle\sum_ r e^{- \beta \epsilon_r }\right)$

alpha =-ln( N )+ln(sum_ r e^(- beta * epsilon_r ))

(ID 3735)

$\ln Z_{MB} = N \ln\left(\displaystyle\sum_ r e^{- \beta \epsilon_r }\right)$

ln Z_MB = N *ln(sum_ r e^(- beta * epsilon_r ))

(ID 3736)

$Z_{BE/FD} =\displaystyle\frac{1}{ N !} Z_{MB}$

Z_BE_FD = Z_MB / N !

(ID 3737)

Beispiele

Ocupaci n de estados

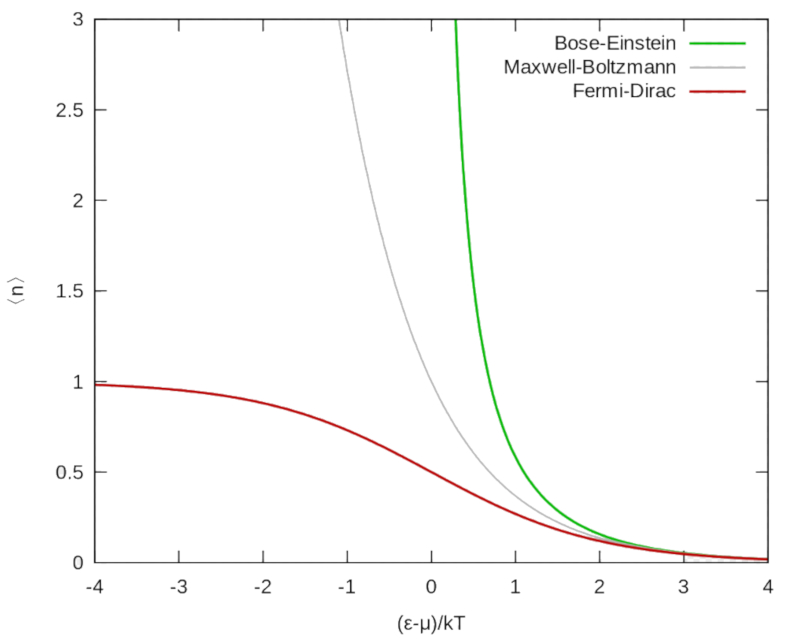
Si se compara la ocupaci n de estados se obtiene que

- la distribuci n de Fermi-Direc (FD) disminuye con la energ a por temperatura
- la distribuci n de Bose Einstein (BE) aumenta con la energ a por temperatura
- la distribuci n de Maxwell-Boltzmann (MB) muestra un comportamiento intermedio
- ambas distribuciones de los gases cuanticos (FD, BE) convergen a alta energ a por temperatura a la distribuci n de Maxwell Boltzmann

(ID 13508)

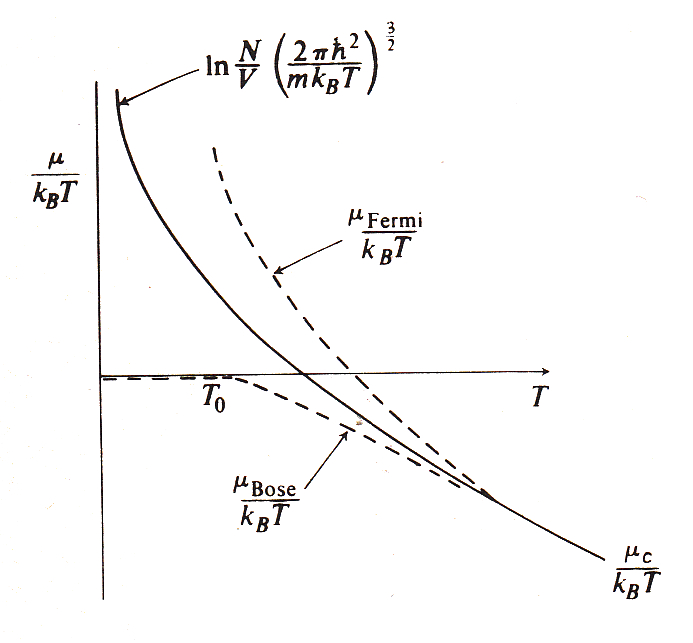
Potencial qu mico en las tres distribuciones

En el caso del potencial qu mico se observa

- en la distribuci n de Fermi-Direc (FD) que decrece al aumentar la temperatura volvi ndose negativo
- en la distribuci n de Bose Einstein (BE) que presenta el condensado (en que es cero) y de igual forma decrece con el aumento de la temperatura
- en la distribuci n de Maxwell-Boltzmann (MB) muestra un comportamiento intermedio
- ambas distribuciones de los gases cuanticos (FD, BE) convergen a alta energ a por temperatura altas a la distribuci n de Maxwell Boltzmann

(ID 13509)

ID:(514, 0)