Storyboard

Paramagnetics sind Materialien, die unter einem externen Magnetfeld polarisieren und ein eigenes Magnetfeld erzeugen. Dies ist jedoch nicht dauerhaft, dh wenn sie aus dem externen Feld entfernt werden, kehren sie in einen Zustand magnetischer Depolarisation zurück.

>Modell

ID:(488, 0)

Bild

>Top

Der Paramagnetismus beschreibt ein Verhalten, bei dem Materialien in Abhängigkeit von einem angelegten externen Magnetfeld magnetisiert werden können. In diesem Sinne bleiben sie nicht dauerhaft magnetisiert und verlieren diese Eigenschaft, sobald das externe Feld entfernt wird.

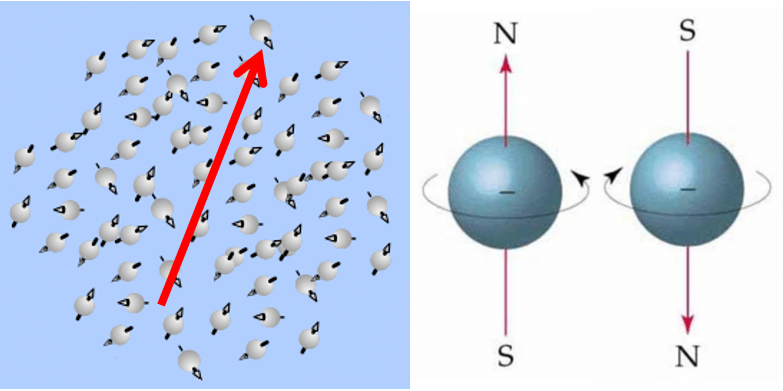
Beispiele für Materialien mit paramagnetischen Eigenschaften sind Magnesium, Molybdän, Lithium und Tantal.

ID:(12106, 0)

Bild

>Top

Paramagnetismus beschreibt ein Verhalten, bei dem Materialien sich unter Einwirkung eines äußeren Magnetfelds magnetisieren können, aber die Magnetisierung nicht beibehalten, wenn das äußere Magnetfeld entfernt wird.

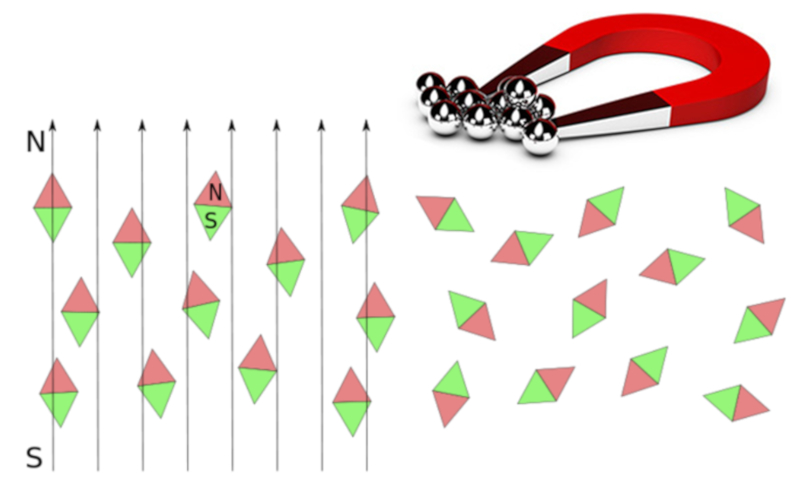
Der Paramagnetismus stammt von drei Arten von magnetischen Momenten:

• Das magnetische Moment des Kerns (bezeichnet als $\mu_n$)
• Das magnetische Moment der Elektronen (bezeichnet als $\mu_s$)
• Das magnetische Moment, das sich aus der Bewegung der Elektronen in den Orbitalen ergibt (bezeichnet als $\mu_l$)

Das erste dieser magnetischen Momente ist in der Regel wesentlich kleiner als die anderen beiden und wird oft vernachlässigt. Das Gesamtmagnetmoment der Elektronen ($S$) und Orbitale ($L$) kann mit der Formel berechnet werden:

$\mu_{L+S}=\sqrt{4S(S+1)+L(L+1)}\mu_B$

wobei $\mu_B$ das Bohrsche Magneton ist.

ID:(12107, 0)

Bild

>Top

Jedes Element kann als ferromagnetisch, paramagnetisch oder diamagnetisch klassifiziert werden, wobei unterschiedliche Empfindlichkeitsgrade zur Magnetisierung auftreten. Elemente, die ferromagnetisch, paramagnetisch oder diamagnetisch sind, können anhand ihrer magnetischen Eigenschaften identifiziert werden, und es ist wichtig, die entsprechenden Skalen bei der Verwendung dieser Werte zu berücksichtigen.

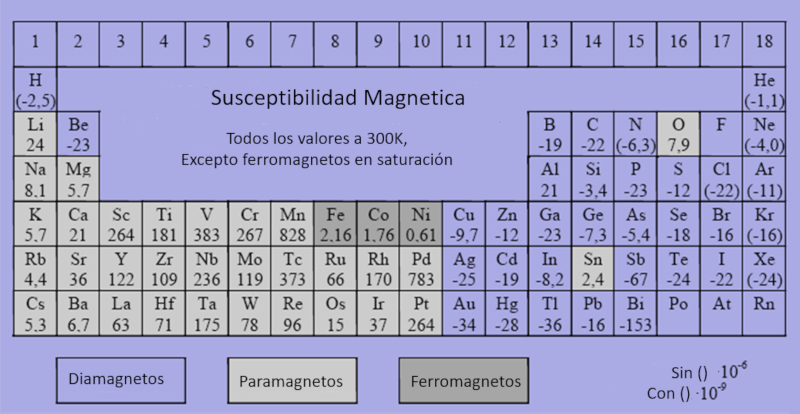
Allgemeine Informationen zu diesen Klassifikationen können in zusätzlichen Ressourcen abgerufen werden unter: Datos.

ID:(12117, 0)

Gleichung

>Top, >Modell

La energía magnética de un átomo \epsilon se puede calcular con de

en donde \vec{\mu} es el momento magnético y \vec{H} es el campo magnético.

ID:(3655, 0)

Gleichung

>Top, >Modell

El momento magnético de un átomo es con igual a

\\n\\ndonde \\n\\n

$\gamma\equiv\displaystyle\frac{e}{2m_e}=8.7821\times 10^{10} C/kg$

es el radio giroscópico, con e la carga del electrón, y m_e la masa del electrón.

ID:(3656, 0)

Gleichung

>Top, >Modell

Si el campo esta en dirección \hat{z} solo sera relevante la componente del Spin en esta dirección. Sus valores serán múltiplos de la constante de Planck dividida por 2\pi o sea con

con m=-s,-s+1,\ldots,s-1,s.

ID:(12109, 0)

Gleichung

>Top, >Modell

El momento magnético se puede expresa con factor g $-$, momento magnético $C m^2/s$ und radio giroscópico $C/kg$ del orden de uno:

Si el campo esta orientado en dirección del eje z se puede reescribir con componente $z$ del spin $kg m^2/s$, constante de Planck dividia con $2\pi$ $J s$ und numero cuántico $-$ el spin

\\n\\ny con ello la energía como\\n\\n

$\epsilon=-g\gamma\vec{S}\cdot\vec{H}=-g\gamma HS_z=-g\gamma\hbar Hm$

\\n\\nSi se introduce el magneto de Bohr como\\n\\n

$\mu_B=\gamma\hbar=\displaystyle\frac{e\hbar}{2m_e}=9.2613\times 10^{-24} C m^2/s$

se tiene que la energía pueden asumir con componente $z$ del spin $kg m^2/s$, constante de Planck dividia con $2\pi$ $J s$ und numero cuántico $-$ los valores

ID:(3657, 0)

Gleichung

>Top, >Modell

Con la definición de la función partición para un sistema en que los elementos no se sobreponen con

y los niveles de energía están definidos con campo magnético $C/m s$, energía del spin en el campo externo $J$, magneton de Bohr $C m^2/s$ und numero cuántico $-$

se puede escribir la función partición para el sistema de N átomos con campo magnético $C/m s$, energía del spin en el campo externo $J$, magneton de Bohr $C m^2/s$ und numero cuántico $-$ como

ID:(3658, 0)

Gleichung

>Top, >Modell

Por analogía el campo magnético cumple el rol de variable mientras que el momento magnético la de una fuerza generalizada es con es

ID:(3661, 0)

Gleichung

>Top, >Modell

La suma de una expresión del tipo\\n\\n

$Z=\displaystyle\sum_{m=-s}^s e^{-\eta m}$

\\n\\nse puede escribir como dos sumas desde 0 a -s y 0 a s restando el elemento 0 que se estaría sumando dos veces\\n\\n

$Z=\displaystyle\sum_{m=-s}^0 e^{-\eta m}+\displaystyle\sum_{m=0}^s e^{-\eta m}-1$

\\n\\nRealizando un cambio de variable (m>-m) en la primera suma se obtiene\\n\\n

$Z=\displaystyle\sum_{m=0}^s e^{\eta m}+\displaystyle\sum_{m=0}^s e^{-\eta m}-1$

\\n\\nDado que las sumas corresponden a series geométricas finitas se tiene que\\n\\n

$\displaystyle\sum_{m=0}^s e^{\eta m}=\displaystyle\frac{1-e^{(s+1)\eta}}{1-e^{\eta}}$

\\n\\ny\\n\\n

$\displaystyle\sum_{m=0}^s e^{-\eta m}=\displaystyle\frac{1-e^{-(s+1)\eta}}{1-e^{-\eta}}$

\\n\\nlo que da\\n\\n

$Z=\displaystyle\frac{1-e^{(s+1)\eta}}{1-e^{\eta}}+\displaystyle\frac{1-e^{-(s+1)\eta}}{1-e^{-\eta}}-1$

\\n\\nComo\\n\\n

$\displaystyle\frac{1-e^{-(s+1)\eta}}{1-e^{-\eta}}-1=\displaystyle\frac{1-e^{-\eta s}}{e^{\eta}-1}$

\\n\\nla expresión se puede reescribir como\\n\\n

$Z=\displaystyle\frac{1-e^{(s+1)\eta}}{1-e^{\eta}}+\displaystyle\frac{1-e^{-\eta s}}{e^{\eta}-1}=\displaystyle\frac{e^{(s+1)\eta}-e^{-\eta s}}{e^{\eta}-1}$

\\n\\nSi multiplicamos numerador y denominador por e^{-\eta/2} resulta\\n\\n

$Z=\displaystyle\frac{e^{(s+1/2)\eta}-e^{-\eta (s+1/2)}}{e^{\eta/2}-e^{-\eta/2}}$

que se puede escribir con la función seno hiperbólico con como

ID:(10727, 0)

Gleichung

>Top, >Modell

Con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ und temperatura $K$ el factor

la función partición en este caso con campo magnético $C/m s$, factor $\beta$ $C m^2/s$, factor g $-$, función de partición del paramagneto $-$, magneton de Bohr $C m^2/s$, numero cuántico $-$, numero cuántico máximo $-$ und números de partículas $-$

se puede sumar con campo magnético $C/m s$, factor $\beta$ $C m^2/s$, factor g $-$, función de partición del paramagneto $-$, magneton de Bohr $C m^2/s$, numero cuántico $-$, numero cuántico máximo $-$ und números de partículas $-$ dando

Por analogía el campo magnético cumple el rol de variable mientras que el momento magnético la de una fuerza generalizada.

ID:(3660, 0)

Gleichung

>Top, >Modell

Con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ und temperatura $K$ el factor

se puede definir una temperatura característica con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ und temperatura $K$

ID:(9553, 0)

Gleichung

>Top, >Modell

Como la energía de un spin en un campo magnético se puede calcular del momento magnético g\mu_0m y con campo magnético $C/m s$, energía del spin en el campo externo $J$ und momento magnético $C m^2/s$ el campo magnético H mediante

se puede asociar el campo magnético con la variable generalizada y el momento magnético con la fuerza generalizada. En tal caso se puede emplear la relación entre fuerza generalizada y función partición con

para calcular el momento magnético medio se puede calcular mediante con :

ID:(3662, 0)

Gleichung

>Top, >Modell

La derivada en el campo magnético del logaritmo de la función con factor $\eta$ $-$, función de partición del paramagneto $-$, numero cuántico máximo $-$ und números de partículas $-$

con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ und temperatura $K$ la definición

\\n\\nes\\n\\n

$\displaystyle\frac{\partial\ln Z}{\partial H}=\displaystyle\frac{\partial\ln Z}{\partial\eta}\displaystyle\frac{\partial\eta}{\partial H}=\displaystyle\frac{g\mu_B}{kT}\frac{\partial\ln Z}{\partial \eta}\equiv \displaystyle\frac{g\mu_B}{kT} B_s(\eta)$

donde con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ und temperatura $K$

ID:(3664, 0)

Gleichung

>Top, >Modell

Como el momento de magnetización medio se calcula con

se tiene para la función partición con factor $\eta$ $-$, función de partición del paramagneto $-$, numero cuántico máximo $-$ und números de partículas $-$

se tiene que con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ und numero cuántico máximo $-$

el momento magnético medio es con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ und numero cuántico máximo $-$

ID:(3659, 0)

Gleichung

>Top, >Modell

En el limite de altas temperaturas el factor \eta tiende a cero por lo que como el cotangente hiperbólico tiende a\\n\\n

$coth(x)\sim\displaystyle\frac{1}{x}+\displaystyle\frac{1}{3}x$

y la función con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ und numero cuántico máximo $-$

tiende con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ und numero cuántico máximo $-$ a

ID:(3663, 0)

Gleichung

>Top, >Modell

El momento magnético con factor g $-$, función de Brillouin de $\eta$ $-$, magneton de Bohr $C m^2/s$, momento magnético medio $C m^2/s$ und números de partículas $-$ es

que en el limite de altas temperaturas, con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ und numero cuántico máximo $-$ en que

y \eta es con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ und temperatura $K$

se tiende con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ und temperatura $K$ a

ID:(9559, 0)

0

Video

Video: Paramagnetismo