Druyd:Knowledge

Función Partición de los Fermiones

Storyboard

>Modell

ID:(503, 0)

Fermi-Funktion für verschiedene Temperaturen

Definition

La función de Fermi tiene el siguiente aspecto:

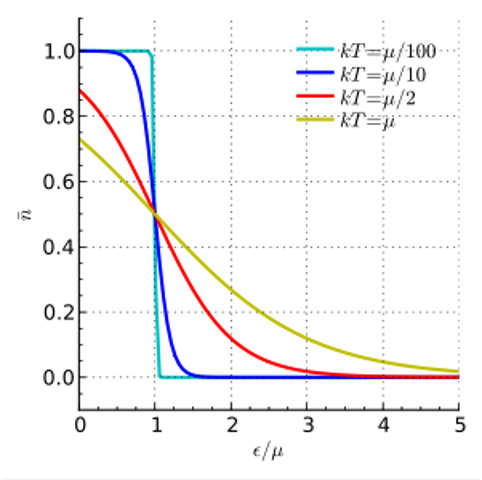
Energía de Fermi

ID:(1923, 0)

Función Partición de los Fermiones

Beschreibung

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$k_B$

k_B

Constante de Boltzmann

J/K

$\hbar$

hbar

Constante de Planck dividida por

$2\pi$

J s

$\epsilon$

epsilon

Energía del electrón

$\epsilon_r$

epsilon_r

Energía del fermion en el estado

$r$

$\alpha$

alpha

Factor alpha

$\beta$

beta

Factor beta

1/J

$\lambda_F$

lambda_F

Largo de onda

$m_e$

m_e

Masa del electrón

$\vec{p}$

Momento (vector)

kg m/s

$n$

Numero de estados

$n_r$

n_r

Numero de fermiones en el estado

$r$

$N$

Numero de partículas

$\epsilon_F$

epsilon_F

Potencial químico del gas de electrones

$T_F$

T_F

Temperatura de Fermi

$k$

Vector de onda

1/m

$\vec{k}$

Vector de onda (vector)

1/m

$k_F$

k_F

Vector de onda de Fermi

1/m

$V$

Volumen

m^3

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$N=\displaystyle\sum_r\displaystyle\frac{1}{e^{\alpha+\beta\epsilon_r}+1}$

N=sum_r 1/(e^(alpha+beta*e_r)+1)

(ID 3729)

$n_r =\displaystyle\frac{1}{e^{ \alpha + \beta \epsilon_r }+1}$

n_r =1/(exp( alpha + beta * epsilon_r )+1)

(ID 3730)

$\vec{p} = \hbar \vec{k}$

&p = hbar * &k

(ID 3793)

$\epsilon =\displaystyle\frac{ \hbar ^2 \vec{k} ^2}{2 m }$

e = hbar ^2 &k ^2/(2* m )

(ID 3794)

$d^3 n =2\displaystyle\frac{ V }{(2 \pi )^3}d^3 k$

d^3 n =2* V /((2* pi )^3)*d^3 k

(ID 3795)

$N =2\displaystyle\frac{ V }{(2 \pi )^3}\displaystyle\frac{4 \pi }{3} k_F ^3$

N =2* V * 4 * pi * k_F ^3/(3*(2 \pi )^3)

(ID 3796)

$k_F =\left(3 \pi ^2\displaystyle\frac{ N }{ V }\right)^{1/3}$

k_F =(3* pi ^2 * N / V )^(1/3)

(ID 3797)

$\lambda_F =\displaystyle\displaystyle\frac{2 \pi }{ k_F }$

lambda_F = 2* pi / k_F

(ID 3798)

$\epsilon_F =\displaystyle\frac{ \hbar ^2}{2 m }\left(3 \pi ^2\displaystyle\frac{ N }{ V }\right)^{2/3}$

epsilon_F = hbar ^2/(2* m )*(3* pi ^2* N / V )^(2/3)

(ID 3799)

$T_F =\displaystyle\frac{ \epsilon_F }{ k_B }$

T_F = epsilon_F / k_B

(ID 3800)

$\displaystyle\sum_ i \rightarrow\displaystyle\frac{ 2 V }{4 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2} \epsilon ^{1/2} d\epsilon$

(ID 13452)

$\ln Z_{FD} = \alpha N + \displaystyle\frac{ V }{2 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2}\displaystyle\int_0^{\infty}\ln(1+e^{- \beta \epsilon - \alpha }) \epsilon ^{1/2} d\epsilon$

ln Z_FD = alpha * N + ( V /2* pi ^2)*(2* m / hbar ^2)^(3/2)*@INTEGARTE(ln(1+exp(- beta * epsilon - alpha ))* epsilon ^(1/2), epsilon , 0 , infty )

(ID 13453)

$N =\displaystyle\frac{ V }{2 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2}\int_0^{\infty}\displaystyle\frac{ \epsilon ^{1/2} d\epsilon }{e^{ \beta \epsilon + \alpha }+1}$

N =\displaystyle\frac{ V }{2 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2}\int_0^{\infty}\displaystyle\frac{ \epsilon ^{1/2} d\epsilon }{e^{ \beta \epsilon + \alpha }+1}

(ID 13680)

Beispiele

Z hlen Zust nden

Si se supone una 'caja' de aristas de largo L los vectores de onda de la funciones de onda ser n iguales a\\n\\n

$k_i=\displaystyle\frac{2\pi}{L}n_i$

\\n\\nPor ello el numero de estados en un volumen en el espacio de estados d^3n es igual a\\n\\n

$d^3 n =\displaystyle\frac{ L ^3}{(2 \pi )^3}d^3 k$

Esta expresi n no considera de que por estado pueden existir dos electrones por lo que debemos incluir un factor 2. Por otro lado la expresi n L^3 corresponde al volumen V por lo que con

$d^3 n =2\displaystyle\frac{ V }{(2 \pi )^3}d^3 k$

en donde m es la masa y \hbar es la constante de Planck devidido por 2\pi.

(ID 3795)

Momentum und Wellenvektor der Elektronen

Cada part cula esta relacionado a un momento \vec{p} que se relaciona con el vector de onda \vec{k}. Con el momento

$\vec{p} = \hbar \vec{k}$

(ID 3793)

Energie der Elektronen

Como los electrones se modelan como part culas libres y podemos asumir el limite no relativista se tiene que la energ a en funci n del vector de onda \vec{k} es con

$\epsilon =\displaystyle\frac{ \hbar ^2 \vec{k} ^2}{2 m }$

en donde m es la masa y \hbar es la constante de Planck devidido por 2\pi.

(ID 3794)

Summe zu Integral

Si consideramos part culas libres en el limite no relativista se puede expresar la energ a \epsilon en funci n del vector de onda k, la constante de Planck \hbar y la masa m:

$\epsilon =\displaystyle\frac{ \hbar ^2 \vec{k} ^2}{2 m }$

\\n\\nLa suma se asocia a la integral del numero de modos\\n\\n

$\displaystyle\sum_i\rightarrow 2\displaystyle\int d^3n$

\\n\\ndonde 2 corresponde los estados spin up y down. Si pasamos al vector de onda se obtiene\\n\\n

$\displaystyle\sum_i\rightarrow \displaystyle\frac{2V}{(2\pi)^3}\int d^3k=\displaystyle\frac{2V}{(2\pi)^3}4\pi\int k^2dk$

Con la relaci n de la energ a con el vector de onda se obtiene con la relaci n

$\displaystyle\sum_ i \rightarrow\displaystyle\frac{ 2 V }{4 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2} \epsilon ^{1/2} d\epsilon$

(ID 13452)

Funci n partici n de Fermiones caso continuo

En el caso continuo la funci n partici n se tiene que con es

$\ln Z_{FD} = \alpha N +\displaystyle\sum_ r \ln(1+e^{- \alpha - \beta \epsilon_r })$

puede re-escribirse con

$\displaystyle\sum_ i \rightarrow\displaystyle\frac{ 2 V }{4 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2} \epsilon ^{1/2} d\epsilon$

con como

(ID 13453)

Anzahl der Partikel in dem Zustand $r$

El n mero de part culas en el estado r se puede calcular con mediante

$\bar{n}_r =-\displaystyle\frac{1}{ \beta }\displaystyle\frac{\partial \ln Z_{BE} }{\partial \epsilon_r }$

con la funci n partici n

$\ln Z_{FD} = \alpha N +\displaystyle\sum_ r \ln(1+e^{- \alpha - \beta \epsilon_r })$

lo que da con

$n_r =\displaystyle\frac{1}{e^{ \alpha + \beta \epsilon_r }+1}$

(ID 3730)

Gesamtzahl der Fermionen

Como la funci n partici n es independiente del factor \alpha se tiene que con

$\ln Z_{FD} = \alpha N +\displaystyle\sum_ r \ln(1+e^{- \alpha - \beta \epsilon_r })$

\\n\\nla derivada de \ln Z_{FD} en \alpha nos da\\n\\n

$\displaystyle\frac{\partial\ln Z_{FD}}{\partial\alpha}=N-\sum_r\displaystyle\frac{e^{-\alpha-\beta\epsilon_r}}{1+e^{-\alpha-\beta\epsilon_r}}$

por lo que el numero de part culas es con

$N=\displaystyle\sum_r\displaystyle\frac{1}{e^{\alpha+\beta\epsilon_r}+1}$

(ID 3729)

Numero de part culas caso continuo

Como el numero de part culas la suma es con energía del fermion en el estado $r$ $J$ , factor alpha $-$ , factor beta $1/J$ und numero de fermiones en el estado $r$ $-$ de

$n_r =\displaystyle\frac{1}{e^{ \alpha + \beta \epsilon_r }+1}$

en el caso continuo con se tiene que

$\displaystyle\sum_ i \rightarrow\displaystyle\frac{ 2 V }{4 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2} \epsilon ^{1/2} d\epsilon$

por lo que con se tiene que

$N =\displaystyle\frac{ V }{2 \pi ^2}\left(\displaystyle\frac{2 m }{ \hbar ^2}\right)^{3/2}\int_0^{\infty}\displaystyle\frac{ \epsilon ^{1/2} d\epsilon }{e^{ \beta \epsilon + \alpha }+1}$

(ID 13680)

Fermi-Funktion f r verschiedene Temperaturen

La funci n de Fermi tiene el siguiente aspecto:

Energ a de Fermi

(ID 1923)

Gesamtzahl der Zust nde

Si se integra el numero d^3n sobre todos los estados se obtiene el numero de electrones N. Como el espacio del vector de onda es isotropico la integraci n sobre \vec{k} da una esfera cuyo radio es igual al vector de onda de Fermi k_F que corresponde al vector de onda de la energ a de Fermi \epsilon_F. Por ello con se tiene que

$N =2\displaystyle\frac{ V }{(2 \pi )^3}\displaystyle\frac{4 \pi }{3} k_F ^3$

(ID 3796)

Broglie Wellenl nge

El largo de onda de Broglie se asocia al vector de onda mediante\\n\\n

$\lambda=\displaystyle\frac{2\pi}{k}$

por lo que se puede definir un largo de onda de Broglie asociado a los electrones mediante el vector de onda de Fermi por lo que con

$\lambda_F =\displaystyle\displaystyle\frac{2 \pi }{ k_F }$

(ID 3798)

Fermi Wellenvektor

Si se despeja la ecuaci n del n mero total de electrones

$N =2\displaystyle\frac{ V }{(2 \pi )^3}\displaystyle\frac{4 \pi }{3} k_F ^3$

se obtiene que el vector de onda de Fermi es con

$k_F =\left(3 \pi ^2\displaystyle\frac{ N }{ V }\right)^{1/3}$

(ID 3797)

Chemisches Potential

Como el potencial qu mico es igual a la energ a de Fermi

$\epsilon =\displaystyle\frac{ \hbar ^2 \vec{k} ^2}{2 m }$

\\n\\ny esta se puede asociar al vector de onda de Fermi se tiene que\\n\\n

$\mu=\displaystyle\frac{\hbar^2k_F^2}{2m}$

Como el n mero de estados se asocia al vector de onda de Fermi mediante

$N =2\displaystyle\frac{ V }{(2 \pi )^3}\displaystyle\frac{4 \pi }{3} k_F ^3$

por lo que el potencial qu mico o la energ a de Fermi es con igual a

$\epsilon_F =\displaystyle\frac{ \hbar ^2}{2 m }\left(3 \pi ^2\displaystyle\frac{ N }{ V }\right)^{2/3}$

(ID 3799)

Fermi Temperatur

Como la energ a \epsilon se puede asociar a la constante de Boltzmann k_B y la temperatura T\\n\\n

$\epsilon=k_BT$

se puede definir una temperatura de Fermi T_F es con

$T_F =\displaystyle\frac{ \epsilon_F }{ k_B }$

(ID 3800)

ID:(503, 0)