Storyboard

Paramagnetics are materials that under an external magnetic field polarize creating their own magnetic field. However this is not permanent, that is to say when they are removed from the external field they return to a state of magnetic depolarization.

>Model

ID:(488, 0)

Image

>Top

Paramagnetism describes a behavior in which materials can be magnetized based on an applied external magnetic field. In this sense, they do not remain magnetized and lose this property as soon as the external field is removed.

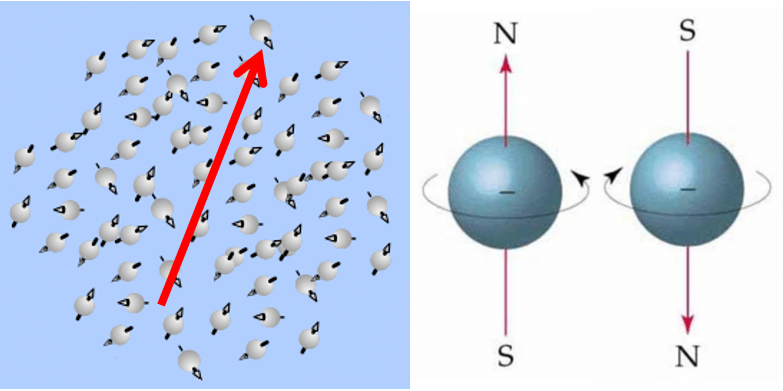
Materials with paramagnetic properties include magnesium, molybdenum, lithium, and tantalum.

ID:(12106, 0)

Image

>Top

Paramagnetism describes a behavior in which materials can become magnetized in response to an applied external magnetic field, but they do not retain the magnetization when the external magnetic field is removed.

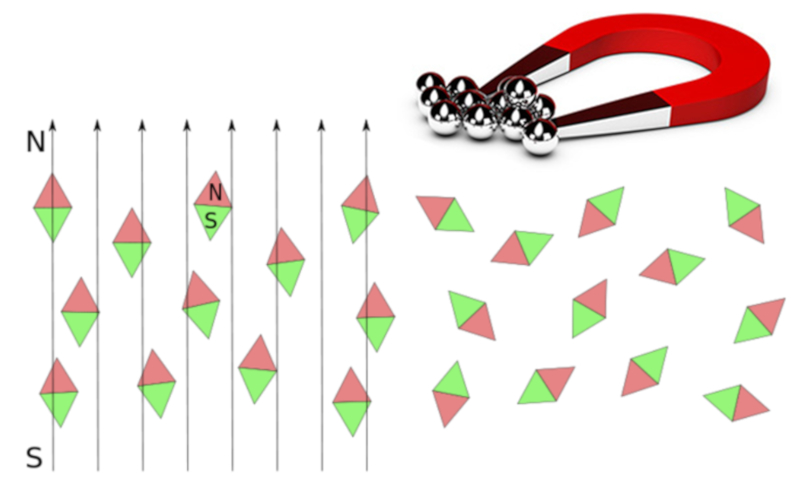
Paramagnetism originates from three types of magnetic moments:

• The magnetic moment of the nucleus (denoted as $\mu_n$)
• The magnetic moment of the electrons (denoted as $\mu_s$)
• The magnetic moment resulting from the motion of electrons in the orbitals (denoted as $\mu_l$)

The first of these magnetic moments is generally much smaller than the other two and is often negligible. The total magnetic moment of the electron ($S$) and orbital ($L$) magnetic moments can be calculated using the formula:

$\mu_{L+S}=\sqrt{4S(S+1)+L(L+1)}\mu_B$

where $\mu_B$ is the Bohr magneton.

ID:(12107, 0)

Image

>Top

Every element can be classified as ferromagnetic, paramagnetic, or diamagnetic with varying levels of magnetization sensitivity. Elements that are ferromagnetic, paramagnetic, or diamagnetic can be identified based on their magnetic properties, and it's important to use the appropriate scales when working with these values.

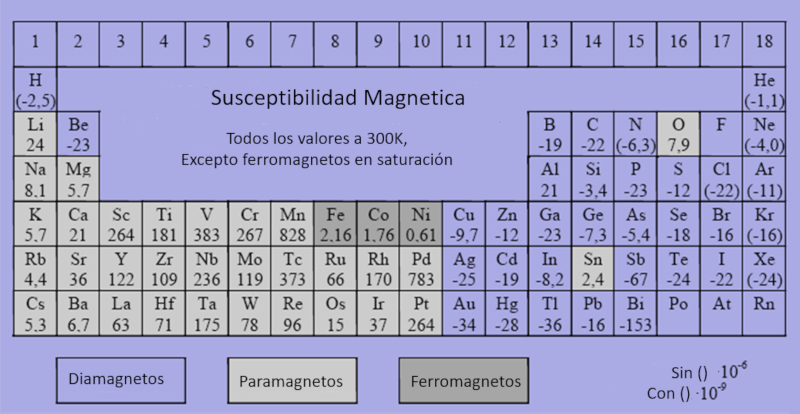
For general data on these classifications, additional resources can be consulted at: Datos.

ID:(12117, 0)

Equation

>Top, >Model

La energía magnética de un átomo \epsilon se puede calcular con de

en donde \vec{\mu} es el momento magnético y \vec{H} es el campo magnético.

ID:(3655, 0)

Equation

>Top, >Model

El momento magnético de un átomo es con igual a

\\n\\ndonde \\n\\n

$\gamma\equiv\displaystyle\frac{e}{2m_e}=8.7821\times 10^{10} C/kg$

es el radio giroscópico, con e la carga del electrón, y m_e la masa del electrón.

ID:(3656, 0)

Equation

>Top, >Model

Si el campo esta en dirección \hat{z} solo sera relevante la componente del Spin en esta dirección. Sus valores serán múltiplos de la constante de Planck dividida por 2\pi o sea con

con m=-s,-s+1,\ldots,s-1,s.

ID:(12109, 0)

Equation

>Top, >Model

El momento magnético se puede expresa con factor g $-$, momento magnético $C m^2/s$ and radio giroscópico $C/kg$ del orden de uno:

Si el campo esta orientado en dirección del eje z se puede reescribir con componente $z$ del spin $kg m^2/s$, constante de Planck dividia con $2\pi$ $J s$ and numero cuántico $-$ el spin

\\n\\ny con ello la energía como\\n\\n

$\epsilon=-g\gamma\vec{S}\cdot\vec{H}=-g\gamma HS_z=-g\gamma\hbar Hm$

\\n\\nSi se introduce el magneto de Bohr como\\n\\n

$\mu_B=\gamma\hbar=\displaystyle\frac{e\hbar}{2m_e}=9.2613\times 10^{-24} C m^2/s$

se tiene que la energía pueden asumir con componente $z$ del spin $kg m^2/s$, constante de Planck dividia con $2\pi$ $J s$ and numero cuántico $-$ los valores

ID:(3657, 0)

Equation

>Top, >Model

Con la definición de la función partición para un sistema en que los elementos no se sobreponen con

y los niveles de energía están definidos con campo magnético $C/m s$, energía del spin en el campo externo $J$, magneton de Bohr $C m^2/s$ and numero cuántico $-$

se puede escribir la función partición para el sistema de N átomos con campo magnético $C/m s$, energía del spin en el campo externo $J$, magneton de Bohr $C m^2/s$ and numero cuántico $-$ como

ID:(3658, 0)

Equation

>Top, >Model

Por analogía el campo magnético cumple el rol de variable mientras que el momento magnético la de una fuerza generalizada es con es

ID:(3661, 0)

Equation

>Top, >Model

La suma de una expresión del tipo\\n\\n

$Z=\displaystyle\sum_{m=-s}^s e^{-\eta m}$

\\n\\nse puede escribir como dos sumas desde 0 a -s y 0 a s restando el elemento 0 que se estaría sumando dos veces\\n\\n

$Z=\displaystyle\sum_{m=-s}^0 e^{-\eta m}+\displaystyle\sum_{m=0}^s e^{-\eta m}-1$

\\n\\nRealizando un cambio de variable (m>-m) en la primera suma se obtiene\\n\\n

$Z=\displaystyle\sum_{m=0}^s e^{\eta m}+\displaystyle\sum_{m=0}^s e^{-\eta m}-1$

\\n\\nDado que las sumas corresponden a series geométricas finitas se tiene que\\n\\n

$\displaystyle\sum_{m=0}^s e^{\eta m}=\displaystyle\frac{1-e^{(s+1)\eta}}{1-e^{\eta}}$

\\n\\ny\\n\\n

$\displaystyle\sum_{m=0}^s e^{-\eta m}=\displaystyle\frac{1-e^{-(s+1)\eta}}{1-e^{-\eta}}$

\\n\\nlo que da\\n\\n

$Z=\displaystyle\frac{1-e^{(s+1)\eta}}{1-e^{\eta}}+\displaystyle\frac{1-e^{-(s+1)\eta}}{1-e^{-\eta}}-1$

\\n\\nComo\\n\\n

$\displaystyle\frac{1-e^{-(s+1)\eta}}{1-e^{-\eta}}-1=\displaystyle\frac{1-e^{-\eta s}}{e^{\eta}-1}$

\\n\\nla expresión se puede reescribir como\\n\\n

$Z=\displaystyle\frac{1-e^{(s+1)\eta}}{1-e^{\eta}}+\displaystyle\frac{1-e^{-\eta s}}{e^{\eta}-1}=\displaystyle\frac{e^{(s+1)\eta}-e^{-\eta s}}{e^{\eta}-1}$

\\n\\nSi multiplicamos numerador y denominador por e^{-\eta/2} resulta\\n\\n

$Z=\displaystyle\frac{e^{(s+1/2)\eta}-e^{-\eta (s+1/2)}}{e^{\eta/2}-e^{-\eta/2}}$

que se puede escribir con la función seno hiperbólico con como

ID:(10727, 0)

Equation

>Top, >Model

Con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ and temperatura $K$ el factor

la función partición en este caso con campo magnético $C/m s$, factor $\beta$ $C m^2/s$, factor g $-$, función de partición del paramagneto $-$, magneton de Bohr $C m^2/s$, numero cuántico $-$, numero cuántico máximo $-$ and números de partículas $-$

se puede sumar con campo magnético $C/m s$, factor $\beta$ $C m^2/s$, factor g $-$, función de partición del paramagneto $-$, magneton de Bohr $C m^2/s$, numero cuántico $-$, numero cuántico máximo $-$ and números de partículas $-$ dando

Por analogía el campo magnético cumple el rol de variable mientras que el momento magnético la de una fuerza generalizada.

ID:(3660, 0)

Equation

>Top, >Model

Con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ and temperatura $K$ el factor

se puede definir una temperatura característica con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ and temperatura $K$

ID:(9553, 0)

Equation

>Top, >Model

Como la energía de un spin en un campo magnético se puede calcular del momento magnético g\mu_0m y con campo magnético $C/m s$, energía del spin en el campo externo $J$ and momento magnético $C m^2/s$ el campo magnético H mediante

se puede asociar el campo magnético con la variable generalizada y el momento magnético con la fuerza generalizada. En tal caso se puede emplear la relación entre fuerza generalizada y función partición con

para calcular el momento magnético medio se puede calcular mediante con :

ID:(3662, 0)

Equation

>Top, >Model

La derivada en el campo magnético del logaritmo de la función con factor $\eta$ $-$, función de partición del paramagneto $-$, numero cuántico máximo $-$ and números de partículas $-$

con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ and temperatura $K$ la definición

\\n\\nes\\n\\n

$\displaystyle\frac{\partial\ln Z}{\partial H}=\displaystyle\frac{\partial\ln Z}{\partial\eta}\displaystyle\frac{\partial\eta}{\partial H}=\displaystyle\frac{g\mu_B}{kT}\frac{\partial\ln Z}{\partial \eta}\equiv \displaystyle\frac{g\mu_B}{kT} B_s(\eta)$

donde con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ and temperatura $K$

ID:(3664, 0)

Equation

>Top, >Model

Como el momento de magnetización medio se calcula con

se tiene para la función partición con factor $\eta$ $-$, función de partición del paramagneto $-$, numero cuántico máximo $-$ and números de partículas $-$

se tiene que con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ and numero cuántico máximo $-$

el momento magnético medio es con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ and numero cuántico máximo $-$

ID:(3659, 0)

Equation

>Top, >Model

En el limite de altas temperaturas el factor \eta tiende a cero por lo que como el cotangente hiperbólico tiende a\\n\\n

$coth(x)\sim\displaystyle\frac{1}{x}+\displaystyle\frac{1}{3}x$

y la función con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ and numero cuántico máximo $-$

tiende con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ and numero cuántico máximo $-$ a

ID:(3663, 0)

Equation

>Top, >Model

El momento magnético con factor g $-$, función de Brillouin de $\eta$ $-$, magneton de Bohr $C m^2/s$, momento magnético medio $C m^2/s$ and números de partículas $-$ es

que en el limite de altas temperaturas, con factor $\eta$ $-$, función de Brillouin de $\eta$ $-$ and numero cuántico máximo $-$ en que

y \eta es con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ and temperatura $K$

se tiende con campo magnético $C/m s$, constante de Boltzmann $J/K$, factor $\eta$ $-$, factor g $-$, magneton de Bohr $C m^2/s$ and temperatura $K$ a

ID:(9559, 0)

0

Video

Video: Paramagnetismo