Druyd:Knowledge

Presión Osmótica

Storyboard

La presencia de iones en un soluto también afecta la presión que el sistema ejerce llevando a una reducción de esta. El fenómeno se describe con la llamada presión osmótica que se considera como una presión negativa, es decir una presión que reduce la presión del sistema.

>Modelo

ID:(568, 0)

Presión osmótica y tubo U

Definición

Cuando se coloca una membrana semipermeable en el fondo de un tubo en forma de U y se agrega agua, se puede observar que al agregar material disuelto, la columna con el soluto se eleva:

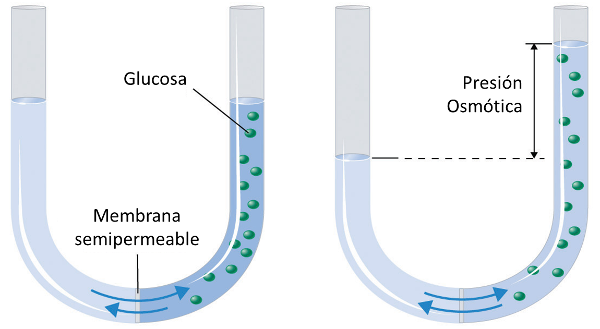
Esto se debe a la presión negativa generada por la presión osmótica.

ID:(2024, 0)

Presión Osmótica

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$k_B$

k_B

Constante de Boltzmann

J/K

$R$

Constante de los gases

J/K mol

$g_0$

g_0

Energía libre molar de Gibbs

$g_{0h}$

g_0h

Energía libre molar de Gibbs solvente con presencia del soluto

$g_0$

g_0

Energía libre molar de Gibbs solvente sin soluto

$N_s$

N_s

Numero de partículas de soluto

$N$

Numero de partículas del solvente

$p$

Presión

$\Psi$

Psi

Presión de las partículas del soluto

$T$

Temperatura

$V$

Volumen

m^3

$v$

Volumen molar

m^3/mol

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ g_0(p,T) = g_0(p',T) -\displaystyle\frac{ N_s }{ N } k_B T $

g_0p = g_0ps - N_s * k_B * T / N

(ID 4064)

$ \Psi =-\displaystyle\frac{ N_s }{ N }\displaystyle\frac{ k_B T }{\left(\displaystyle\displaystyle\frac{\partial g_0 }{\partial p }\right)_T}$

Psi =-( N_s / N )*( k_B * T )/(\partial g_0 }{\partial p }\right)_T

(ID 4154)

$ \Psi =\displaystyle\frac{ n_s }{ V } R T $

Psi = n_s /( V * R * T )

(ID 4155)

$\displaystyle\frac{\partial g_0 }{\partial p }=\displaystyle\frac{ V }{ N }$

\displaystyle\frac{\partial g_0 }{\partial p }=\displaystyle\frac{ V }{ N }

(ID 9045)

Ejemplos

Situaci n con membrana y soluci n

Si consideramos una soluci n con una presi n separada del solvente con puro por una membrana semipermeable los potenciales qu micos deben ser iguales. Si suponemos que la temperatura es igual a ambos lados de la membrana se tendr que con

$ g_0(p,T) = g_0(p',T) -\displaystyle\frac{ N_s }{ N } k_B T $

donde p es la presi n del solvente puro y p' aquella del solvente con soluto. De esta ecuaci n se sigue que ambas presiones p y p' no pueden ser iguales. De hecho, como las funciones molares de Gibbs tienden a subir con la presi n p'>p y el soluto figura con una presi n negativa.

(ID 4064)

Presi n osm tica

Cuando se tiene una membrana que separa solvente puro de solvente con soluto se presentara una presi n negativa que debe ser igual\\n\\n

$\Psi=p-p'$

\\n\\ny que denominaremos presi n osm tica. Para obtener una expresi n para la presi n osm tica basta expandir la funci n molar de Gibbs en $\Psi$:\\n\\n

$g_0(p'+\Psi,T)\sim g_0(p',T)+\left(\displaystyle\frac{\partial g_0}{\partial p}\right)_T\Psi$

lo que en la ecuaci n con constante de Boltzmann $J/K$, energía libre molar de Gibbs solvente con presencia del soluto $J$, energía libre molar de Gibbs solvente sin soluto $J$, numero de partículas de soluto $-$, numero de partículas del solvente $-$ y temperatura $K$

$ g_0(p,T) = g_0(p',T) -\displaystyle\frac{ N_s }{ N } k_B T $

nos deja con constante de Boltzmann $J/K$, energía libre molar de Gibbs solvente con presencia del soluto $J$, energía libre molar de Gibbs solvente sin soluto $J$, numero de partículas de soluto $-$, numero de partículas del solvente $-$ y temperatura $K$

$ \Psi =-\displaystyle\frac{ N_s }{ N }\displaystyle\frac{ k_B T }{\left(\displaystyle\displaystyle\frac{\partial g_0 }{\partial p }\right)_T}$

(ID 4154)

Derivada de la energ a de Gibbs en el volumen

La deriva de la energ a libre de Gibbs respecto de la presi n es igual al volumen\\n\\n

$V=\displaystyle\frac{\partial G}{\partial p}$

por lo que la derivada de la energ a libre de Gibbs por part cula es

$\displaystyle\frac{\partial g_0 }{\partial p }=\displaystyle\frac{ V }{ N }$

(ID 9045)

Comportamiento del soluto como gas ideal

Con la presi n osm tica es con constante de Boltzmann $J/K$, energía libre molar de Gibbs $J$, numero de partículas de soluto $-$, numero de partículas del solvente $-$, presión $Pa$, presión de las partículas del soluto $Pa$ y temperatura $K$ es igual a

$ \Psi =-\displaystyle\frac{ N_s }{ N }\displaystyle\frac{ k_B T }{\left(\displaystyle\displaystyle\frac{\partial g_0 }{\partial p }\right)_T}$

La deriva de la funci n molar de Gibbs se puede reemplazar por el volumen molar con energía libre molar de Gibbs $J$, presión $Pa$ y volumen molar $m^3/mol$ mediante

$\displaystyle\frac{\partial g_0 }{\partial p }=\displaystyle\frac{ V }{ N }$

\\n\\ncon lo que la presi n osm tica es\\n\\n

$ \Psi =-\displaystyle\frac{ N_s }{ V } k_B T $

Si recordamos que la constante de los gases es con

$ R_C = N_A k_B $

se tiene que con

$ \Psi =\displaystyle\frac{ n_s }{ V } R T $

\\n\\ncon n_s el numero de moles del soluto\\n\\n

$n_s=\displaystyle\frac{N_s}{N_A}$

Esta ecuaci n tiene la forma de una ecuaci n de los gases ideales o sea las mol culas de soluto en suspensi n se comportan como un gas ideal.

(ID 4155)

Presi n osm tica y tubo U

Cuando se coloca una membrana semipermeable en el fondo de un tubo en forma de U y se agrega agua, se puede observar que al agregar material disuelto, la columna con el soluto se eleva:

Esto se debe a la presi n negativa generada por la presi n osm tica.

(ID 2024)

ID:(568, 0)