User:
Balance Condition and Temperature
Storyboard 
To model systems using statistical mechanics, we need to investigate how statistical ensembles can be influenced by the parameters that describe the macroscopic system. For particles, temperature is established as a parameter that reflects whether systems are in equilibrium, maintaining their energies at a constant level.
ID:(436, 0)
A System in contact with a reservoir
Image
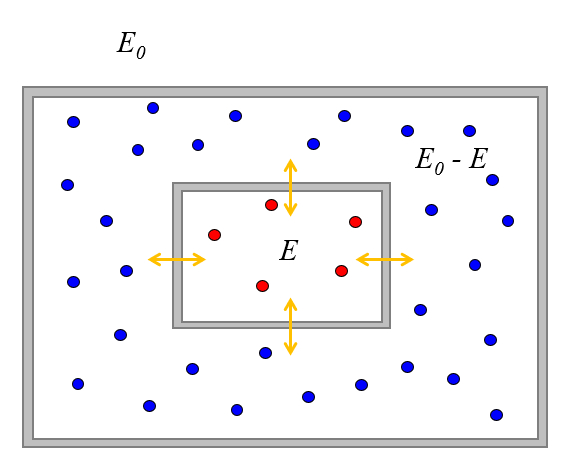
We can study what happens when we put two systems of particles in contact in such a way that they can exchange energy but not particles.
Let's also assume that the system is isolated from the surroundings, meaning it has a total energy of $E_0$.
Suppose initially the first system has an energy of $E$, which is associated with $\Omega(E)$ states.
Since the total energy is $E_0$, the second system can only have the energy $E_0-E" and a number of associated states $\Omega(E_0-E)$.
Once we bring them into contact, they can exchange energy until they reach some equilibrium. In this regard, the value of $E$ will vary, and the probability of finding the systems such that the first one has a value of $E$ will also vary.
ID:(11541, 0)
Comparing the number of state curves
Image
When we compare how the number of states varies with energy $E$, we observe that the behavior of the system and the reservoir is opposite:
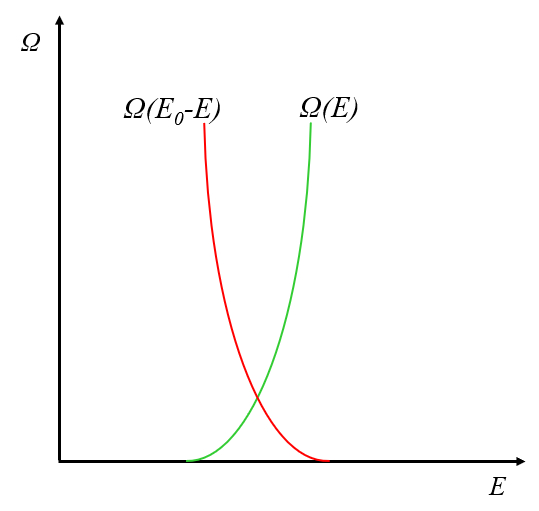
This happens because as the energy increases, the energy of the reservoir decreases, leading to a reduction in the number of states it can access.
ID:(11542, 0)
Forming a maximum
Image
When we multiply the number of cases, we obtain a function with a very pronounced peak.
The system is more likely to be found at the energy where the peak of the probability curve occurs.
ID:(11543, 0)
Balance Condition and Temperature
Model
To model systems using statistical mechanics, we need to investigate how statistical ensembles can be influenced by the parameters that describe the macroscopic system. For particles, temperature is established as a parameter that reflects whether systems are in equilibrium, maintaining their energies at a constant level.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
(ID 3438)
Examples
We can study what happens when we put two systems of particles in contact in such a way that they can exchange energy but not particles.
Let's also assume that the system is isolated from the surroundings, meaning it has a total energy of $E_0$.
Suppose initially the first system has an energy of $E$, which is associated with $\Omega(E)$ states.
Since the total energy is $E_0$, the second system can only have the energy $E_0-E" and a number of associated states $\Omega(E_0-E)$.
Once we bring them into contact, they can exchange energy until they reach some equilibrium. In this regard, the value of $E$ will vary, and the probability of finding the systems such that the first one has a value of $E$ will also vary.
(ID 11541)
When we compare how the number of states varies with energy $E$, we observe that the behavior of the system and the reservoir is opposite:
This happens because as the energy increases, the energy of the reservoir decreases, leading to a reduction in the number of states it can access.
(ID 11542)
When we multiply the number of cases, we obtain a function with a very pronounced peak.
The system is more likely to be found at the energy where the peak of the probability curve occurs.
(ID 11543)
ID:(436, 0)