Usuario:


Partícula en una caja y esfera
Storyboard

Cuando consideramos una partícula dentro de un volumen, ya sea una caja o una esfera, podemos calcular la probabilidad de encontrar la partícula en un intervalo de posiciones.

>Modelo

ID:(433, 0)


Espacio de fase de una partícula en una caja 1D
Imagen

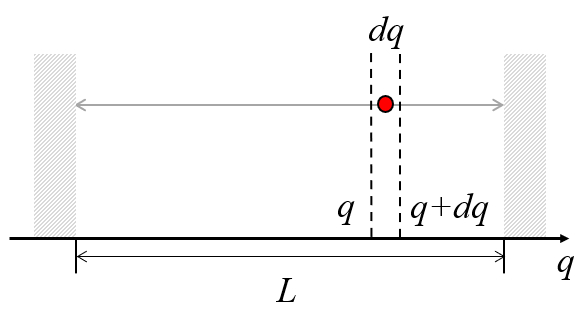
Considere una caja de largo L en que una partícula rebota entre ambas paredes viajando con una momento p:

La pregunta es cual es la probabilidad de encontrarla en un rango dq.

ID:(11463, 0)


Espacio de fase de una partícula en una caja 2D
Imagen

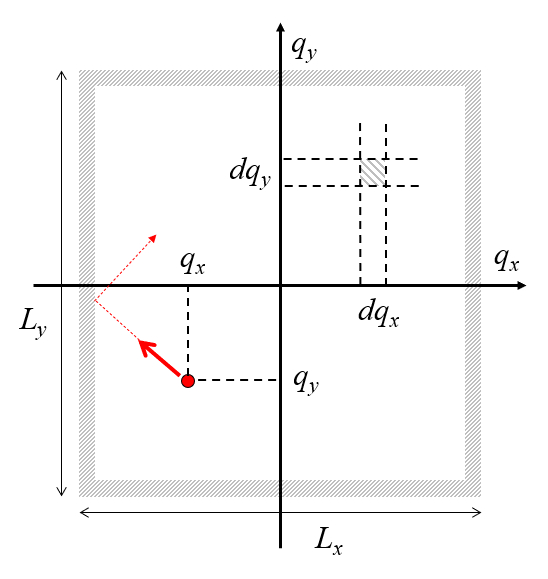
Considere una caja en 2D de largo L_x y ancho L_y en que una partícula rebota entre ambas paredes viajando con una momento (p_x,p_y):

La pregunta es cual es la probabilidad de encontrarla en un cuadrilatero de ancho dq_x y alto dq_y.

ID:(11464, 0)


Espacio de fase de una partícula en una esfera 3D
Imagen

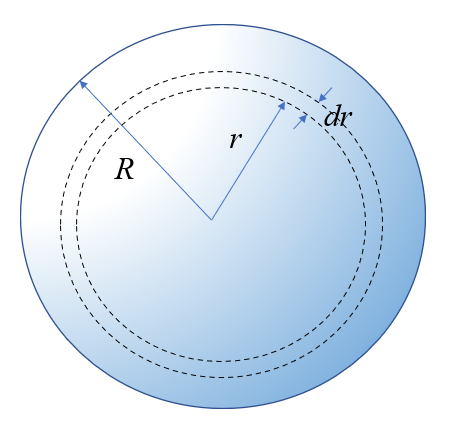
Considere una esfera de radio R en que una partícula rebota entre ambas paredes viajando con una momento (p_x,p_y,p_z):

La pregunta es cual es la probabilidad de encontrarla en una capa de ancho dr.

ID:(11465, 0)


Probabilidad de encontrar la partícula en un radio $r$
Imagen

La probabilidad de encontrar la partícula en un radio entre r y r+dr es con grosor de la capa esférica $m$, probabilidad partícula entre los radios $r$ y $r+dr$ $-$, radio de la esfera $m$ y radio en que se encuentra la partícula $m$

$ P(r) = \displaystyle\frac{3 r ^2}{ R ^3 } dr $



que se muestra en la siguiente gráfica:

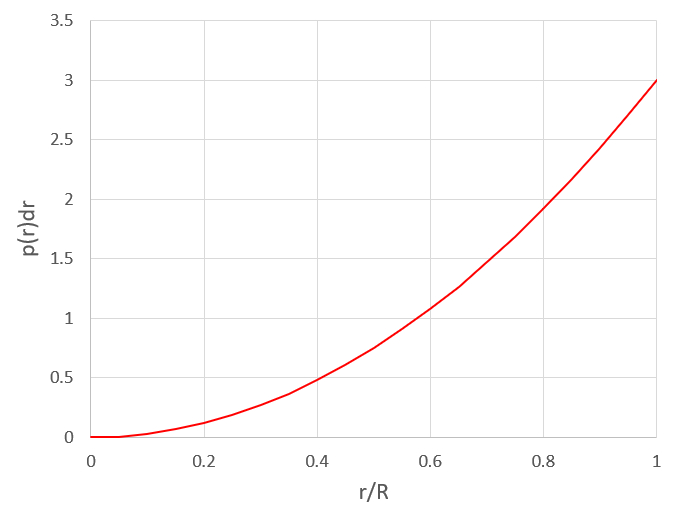
ID:(11466, 0)


Partícula en una caja y esfera
Modelo

Cuando consideramos una partícula dentro de un volumen, ya sea una caja o una esfera, podemos calcular la probabilidad de encontrar la partícula en un intervalo de posiciones.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$dq$
dq
Elemento del largo de la caja
m
$dq_x$
dq_x
Elemento del largo de la caja en dirección x
m
$dq_y$
dq_y
Elemento del largo de la caja en dirección y
m
$dr$
dr
Grosor de la capa esférica
m
$L$
L
Largo de la caja
m
$L_x$
L_x
Largo de la caja en dirección x
m
$L_y$
L_y
Largo de la caja en dirección y
m
$P(q_x,q_y)$
P_qxqy
Probabilidad partícula en el rectángulo de rangos en x e y
-
$P_q$
P_q
Probabilidad partícula entre $q$ y $q+dq$
-
$P(r)$
P_r
Probabilidad partícula entre los radios $r$ y $r+dr$
-
$R$
R
Radio de la esfera
m
$r$
r
Radio en que se encuentra la partícula
m

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Considere una caja de largo L en que una part cula rebota entre ambas paredes viajando con una momento p:

La pregunta es cual es la probabilidad de encontrarla en un rango dq.

(ID 11463)

Considere una caja en 2D de largo L_x y ancho L_y en que una part cula rebota entre ambas paredes viajando con una momento (p_x,p_y):

La pregunta es cual es la probabilidad de encontrarla en un cuadrilatero de ancho dq_x y alto dq_y.

(ID 11464)

Considere una esfera de radio R en que una part cula rebota entre ambas paredes viajando con una momento (p_x,p_y,p_z):

La pregunta es cual es la probabilidad de encontrarla en una capa de ancho dr.

(ID 11465)

La probabilidad de encontrar la part cula en un radio entre r y r+dr es con grosor de la capa esférica $m$, probabilidad partícula entre los radios $r$ y $r+dr$ $-$, radio de la esfera $m$ y radio en que se encuentra la partícula $m$

$ P(r) = \displaystyle\frac{3 r ^2}{ R ^3 } dr $



que se muestra en la siguiente gr fica:

(ID 11466)

ID:(433, 0)