Paramagnetismo
Storyboard 
Paramagnetics are materials that under an external magnetic field polarize creating their own magnetic field. However this is not permanent, that is to say when they are removed from the external field they return to a state of magnetic depolarization.
ID:(488, 0)
Magnetization
Image 
Paramagnetism describes a behavior in which materials can be magnetized based on an applied external magnetic field. In this sense, they do not remain magnetized and lose this property as soon as the external field is removed.
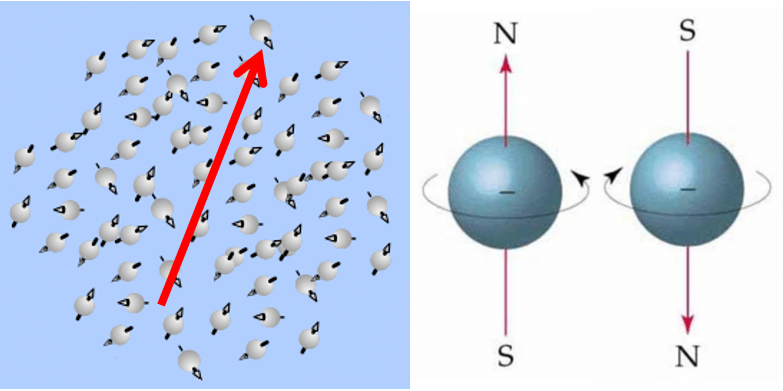
Materials with paramagnetic properties include magnesium, molybdenum, lithium, and tantalum.
ID:(12106, 0)
Paramagnet
Image 
Paramagnetism describes a behavior in which materials can become magnetized in response to an applied external magnetic field, but they do not retain the magnetization when the external magnetic field is removed.
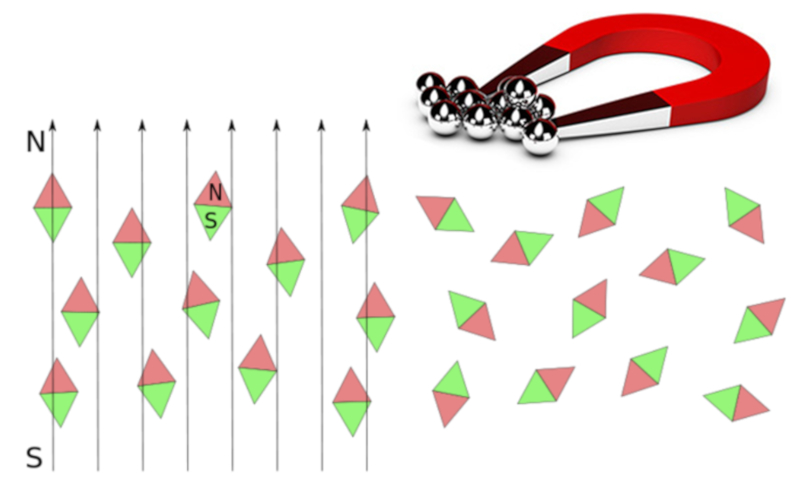
Paramagnetism originates from three types of magnetic moments:
• The magnetic moment of the nucleus (denoted as $\mu_n$)
• The magnetic moment of the electrons (denoted as $\mu_s$)
• The magnetic moment resulting from the motion of electrons in the orbitals (denoted as $\mu_l$)
The first of these magnetic moments is generally much smaller than the other two and is often negligible. The total magnetic moment of the electron ($S$) and orbital ($L$) magnetic moments can be calculated using the formula:
$\mu_{L+S}=\sqrt{4S(S+1)+L(L+1)}\mu_B$
where $\mu_B$ is the Bohr magneton.
ID:(12107, 0)
Ferro, para and diamagnetic materials
Image 
Every element can be classified as ferromagnetic, paramagnetic, or diamagnetic with varying levels of magnetization sensitivity. Elements that are ferromagnetic, paramagnetic, or diamagnetic can be identified based on their magnetic properties, and it's important to use the appropriate scales when working with these values.
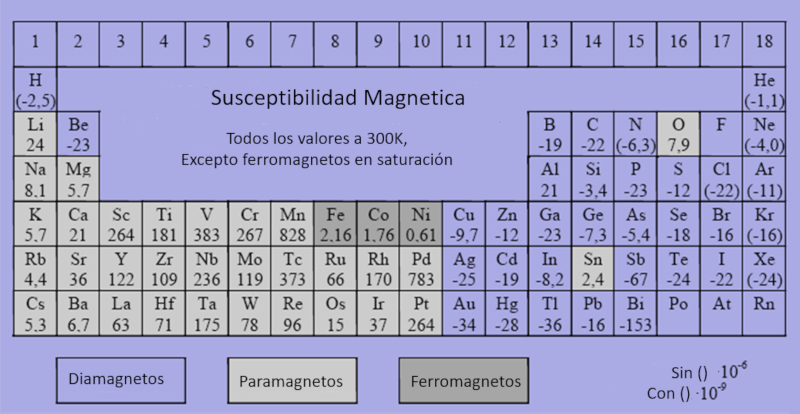
For general data on these classifications, additional resources can be consulted at: Datos.
ID:(12117, 0)
Paramagnetismo
Model 
Paramagnetics are materials that under an external magnetic field polarize creating their own magnetic field. However this is not permanent, that is to say when they are removed from the external field they return to a state of magnetic depolarization.
Variables
Calculations
Calculations
Equations
(ID 12109)
Examples
Paramagnetism describes a behavior in which materials can be magnetized based on an applied external magnetic field. In this sense, they do not remain magnetized and lose this property as soon as the external field is removed.

Materials with paramagnetic properties include magnesium, molybdenum, lithium, and tantalum.
(ID 12106)
Paramagnetism describes a behavior in which materials can become magnetized in response to an applied external magnetic field, but they do not retain the magnetization when the external magnetic field is removed.

Paramagnetism originates from three types of magnetic moments:
• The magnetic moment of the nucleus (denoted as $\mu_n$)
• The magnetic moment of the electrons (denoted as $\mu_s$)
• The magnetic moment resulting from the motion of electrons in the orbitals (denoted as $\mu_l$)
The first of these magnetic moments is generally much smaller than the other two and is often negligible. The total magnetic moment of the electron ($S$) and orbital ($L$) magnetic moments can be calculated using the formula:
$\mu_{L+S}=\sqrt{4S(S+1)+L(L+1)}\mu_B$
where $\mu_B$ is the Bohr magneton.
(ID 12107)
Every element can be classified as ferromagnetic, paramagnetic, or diamagnetic with varying levels of magnetization sensitivity. Elements that are ferromagnetic, paramagnetic, or diamagnetic can be identified based on their magnetic properties, and it's important to use the appropriate scales when working with these values.

For general data on these classifications, additional resources can be consulted at: Datos.
(ID 12117)
ID:(488, 0)
