Utilisateur:
Condition d'équilibre et température
Storyboard 
Pour modéliser des systèmes à l'aide de la mécanique statistique, il est nécessaire d'étudier comment les paramètres qui décrivent le système macroscopique peuvent influencer les ensembles statistiques. Dans le cas des particules, la température est établie comme un paramètre qui reflète si les systèmes sont en équilibre, maintenant leurs énergies à un niveau constant.
ID:(436, 0)
Un système en contact avec un réservoir
Image
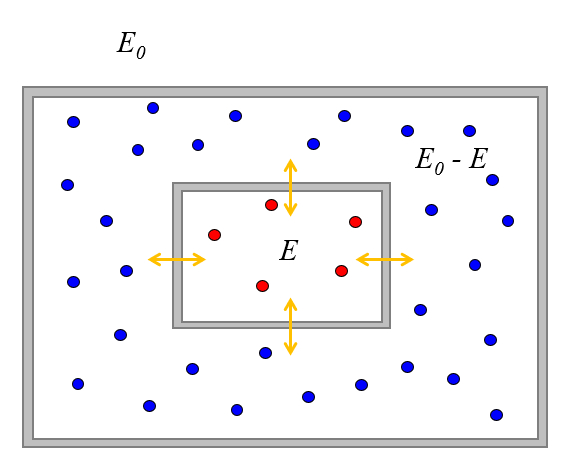
Nous pouvons étudier ce qui se passe lorsque nous mettons en contact deux systèmes de particules de manière à ce qu'ils puissent échanger de l'énergie mais pas de particules.
Supposons également que le système soit isolé de son environnement, ce qui signifie qu'il a une énergie totale de $E_0$.
Supposons qu'initialement le premier système ait une énergie de $E$, ce qui est associé à $\Omega(E)$ états.
Étant donné que l'énergie totale est de $E_0$, le second système ne peut avoir que l'énergie $E_0-E$ et un certain nombre d'états associés $\Omega(E_0-E)$.
Une fois que nous les mettons en contact, ils peuvent échanger de l'énergie jusqu'à ce qu'ils atteignent un certain équilibre. À cet égard, la valeur de $E$ va varier, et la probabilité de trouver les systèmes de telle sorte que le premier ait une valeur de $E$ va également varier.
ID:(11541, 0)
Comparaison des courbes du nombre d'états
Image
Lorsque nous comparons la variation du nombre d'états en fonction de l'énergie $E$, nous remarquons que le comportement du système et du réservoir est opposé :
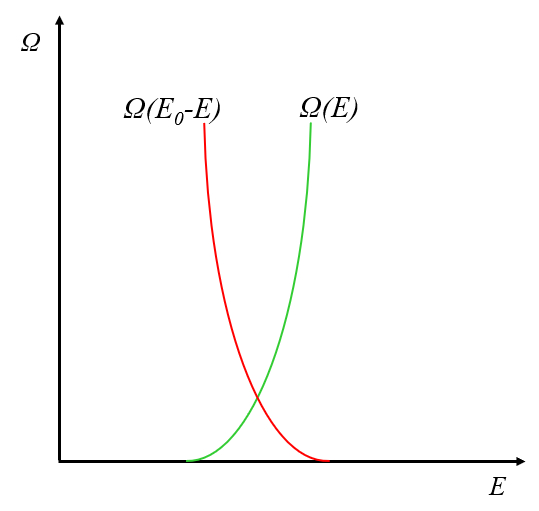
Cela se produit parce qu'à mesure que l'énergie augmente, celle du réservoir diminue, ce qui réduit le nombre d'états auxquels il peut accéder.
ID:(11542, 0)
Formation d'un maximum
Image
Lorsque nous multiplions le nombre de cas, nous obtenons une fonction avec un pic très marqué.
Le système a plus de chances d'être trouvé à l'énergie où se situe le pic de la courbe de probabilité.
ID:(11543, 0)
Condition d'équilibre et température
Modèle
Pour modéliser des systèmes à l'aide de la mécanique statistique, il est nécessaire d'étudier comment les paramètres qui décrivent le système macroscopique peuvent influencer les ensembles statistiques. Dans le cas des particules, la température est établie comme un paramètre qui reflète si les systèmes sont en équilibre, maintenant leurs énergies à un niveau constant.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
(ID 3438)
Exemples
Nous pouvons tudier ce qui se passe lorsque nous mettons en contact deux syst mes de particules de mani re ce qu'ils puissent changer de l' nergie mais pas de particules.
Supposons galement que le syst me soit isol de son environnement, ce qui signifie qu'il a une nergie totale de $E_0$.
Supposons qu'initialement le premier syst me ait une nergie de $E$, ce qui est associ $\Omega(E)$ tats.
tant donn que l' nergie totale est de $E_0$, le second syst me ne peut avoir que l' nergie $E_0-E$ et un certain nombre d' tats associ s $\Omega(E_0-E)$.
Une fois que nous les mettons en contact, ils peuvent changer de l' nergie jusqu' ce qu'ils atteignent un certain quilibre. cet gard, la valeur de $E$ va varier, et la probabilit de trouver les syst mes de telle sorte que le premier ait une valeur de $E$ va galement varier.
(ID 11541)
Lorsque nous comparons la variation du nombre d' tats en fonction de l' nergie $E$, nous remarquons que le comportement du syst me et du r servoir est oppos :
Cela se produit parce qu' mesure que l' nergie augmente, celle du r servoir diminue, ce qui r duit le nombre d' tats auxquels il peut acc der.
(ID 11542)
Lorsque nous multiplions le nombre de cas, nous obtenons une fonction avec un pic tr s marqu .
Le syst me a plus de chances d' tre trouv l' nergie o se situe le pic de la courbe de probabilit .
(ID 11543)
ID:(436, 0)