User:


Particle in a box and sphere
Storyboard

When we consider a particle within a volume, whether it's a box or a sphere, we can estimate the probability of finding the particle within a range of positions.

>Model

ID:(433, 0)


Particle in a box and sphere
Description

When we consider a particle within a volume, whether it's a box or a sphere, we can estimate the probability of finding the particle within a range of positions.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$dq$
dq
Elemento del largo de la caja
m
$dq_x$
dq_x
Elemento del largo de la caja en dirección x
m
$dq_y$
dq_y
Elemento del largo de la caja en dirección y
m
$dr$
dr
Grosor de la capa esférica
m
$L$
L
Largo de la caja
m
$L_x$
L_x
Largo de la caja en dirección x
m
$L_y$
L_y
Largo de la caja en dirección y
m
$P(q_x,q_y)$
P_qxqy
Probabilidad partícula en el rectángulo de rangos en x e y
-
$P_q$
P_q
Probabilidad partícula entre $q$ y $q+dq$
-
$P(r)$
P_r
Probabilidad partícula entre los radios $r$ y $r+dr$
-
$R$
R
Radio de la esfera
m
$r$
r
Radio en que se encuentra la partícula
m

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Examples

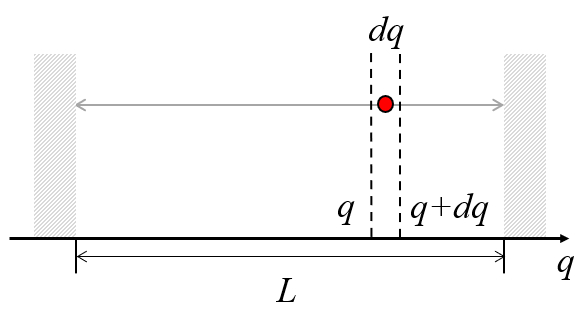
Consider a box of length L in which a particle bounces between both walls traveling with a p moment:

The question is what is the probability of finding it in a dq range.

(ID 11463)

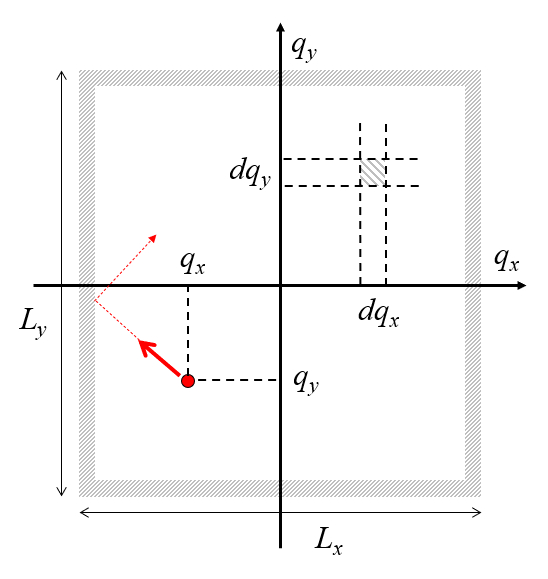
Consider a 2D box of length L_x and width L_y in which a particle bounces between both walls traveling with a (p_x,p_y) moment:

The question is what is the probability of finding it in a quadrilateral of width dq_x and height dq_y.

(ID 11464)

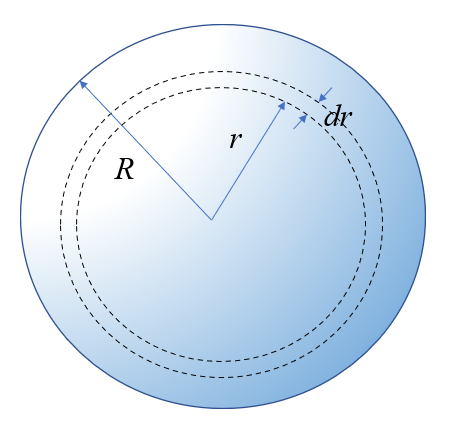
Consider a sphere of radius R in which a particle bounces between both walls traveling with a moment (p_x,p_y,p_z):

The question is what is the probability of finding it in a quadrilateral of width dq_x and height dq_y.

(ID 11465)

La probabilidad de encontrar la part cula en un radio entre r y r+dr es con grosor de la capa esférica $m$, probabilidad partícula entre los radios $r$ y $r+dr$ $-$, radio de la esfera $m$ and radio en que se encuentra la partícula $m$

$ P(r) = \displaystyle\frac{3 r ^2}{ R ^3 } dr $



que se muestra en la siguiente gr fica:

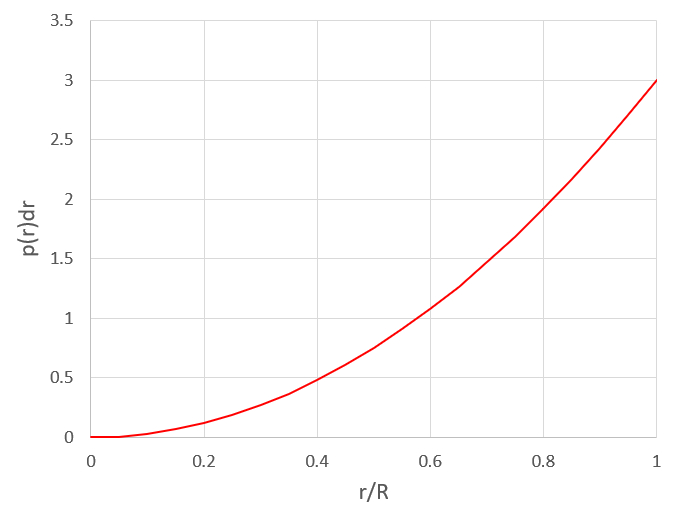
(ID 11466)

ID:(433, 0)