Example of the Random Path (Rando Walk)
Storyboard 
The random path is a typical example as starting from microscopic probabilities (the step to the right or left) it is possible to develop a probability distribution that accounts for the most probable places in which the walker can be found.
ID:(308, 0)
Random walk problem
Image 
The problem of the random path is an example of how one can from the microscopic description predict the probable temporal evolution. In this case it is assumed that an actor (particle, person, etc.) randomly chooses whether to take a step to the right or to the left. It is assumed that the steps have a length
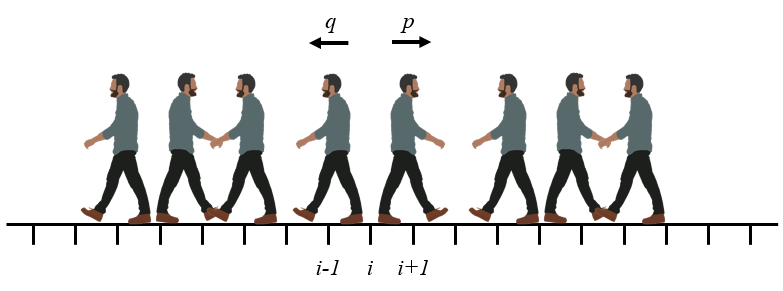
ID:(11396, 0)
Binomial distribution
Image 
The result of the calculation corresponds to what is called a binomial distribution. Each line indicates the fraction of times that after a number
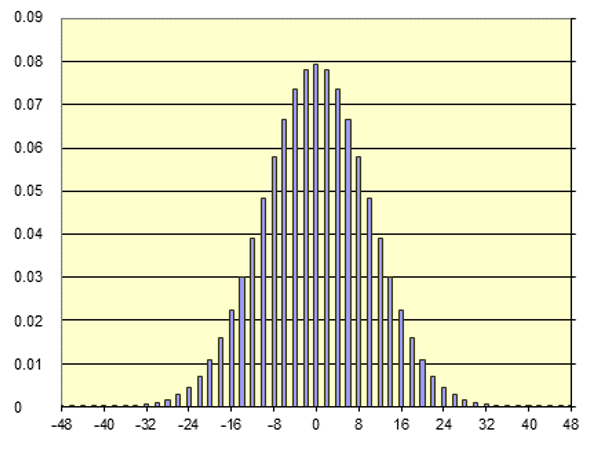
ID:(11397, 0)
Example of the Random Path (Rando Walk)
Model 
The random path is a typical example as starting from microscopic probabilities (the step to the right or left) it is possible to develop a probability distribution that accounts for the most probable places in which the walker can be found.
Variables
Calculations
Calculations
Equations
(ID 501)
(ID 503)
(ID 3358)
(ID 8965)
Examples
The problem of the random path is an example of how one can from the microscopic description predict the probable temporal evolution. In this case it is assumed that an actor (particle, person, etc.) randomly chooses whether to take a step to the right or to the left. It is assumed that the steps have a length

(ID 11396)
The result of the calculation corresponds to what is called a binomial distribution. Each line indicates the fraction of times that after a number

(ID 11397)
ID:(308, 0)
