Snells Gesetz
Storyboard 
Das Snellsche Gesetz ermöglicht es, den Winkel zu bestimmen, mit dem ein Lichtstrahl gebrochen (abgelenkt) wird, basierend auf den Eigenschaften beider Medien.
Die Eigenschaften beider Mittel beziehen sich auf den Brechungsindex oder die Ausbreitungsgeschwindigkeit im jeweiligen Medium.
ID:(302, 0)
Brechungsindexänderung
Definition 
Cuando la luz en un medio con velocidad de la luz
La transmisión sin embargo no solo puede perder intensidad, por la fracción reflejada, también puede ser desviada. Este desvío se denomina refracción.
ID:(429, 0)
Principio de Huygens: refracción de la luz
Bild 
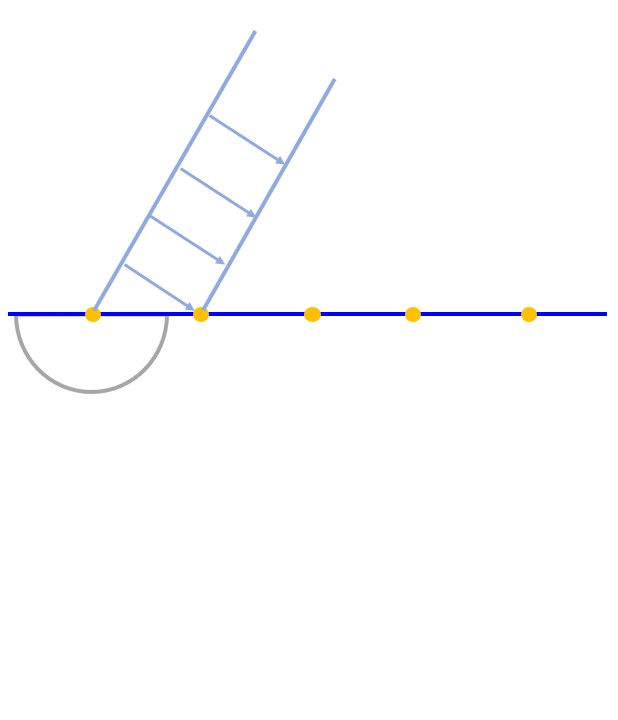
Para aplicar el principio de Huygens en el caso del paso de luz de un medio a un segundo en que la velocidad de la luz varia, se debe considerar fuentes que gatillada en el primero y genera ondas esféricas en el segundo:
ID:(12667, 0)
Principio de Huygens: creación de segunda fuente y radiación de la primera
Notiz 
A medida que se crea la segunda fuente la primera ya ha irradiado:

Eso si se debe tener presente que al ser las velocidades distintas el tamaño de la radiación esférica es de diferente tamaño en los dos medios.
ID:(12668, 0)
Principio de Huygens: nuevas fuentes y mas radiación en el segundo medio
Zitat 
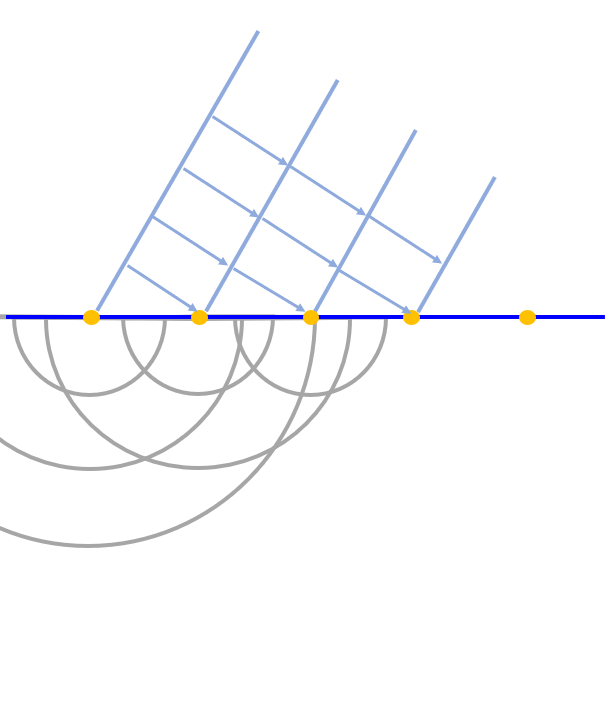
Continuando se va viendo como se comienza a generar un nuevo frente de onda que no presenta la misma orientación que el primero:
ID:(12669, 0)
Principio de Huygens: el cambio en el frente de onda
Übung 
Finalmente se pueden dibujar los frentes de onda quedando claro que la dirección de propagación ha cambiado:
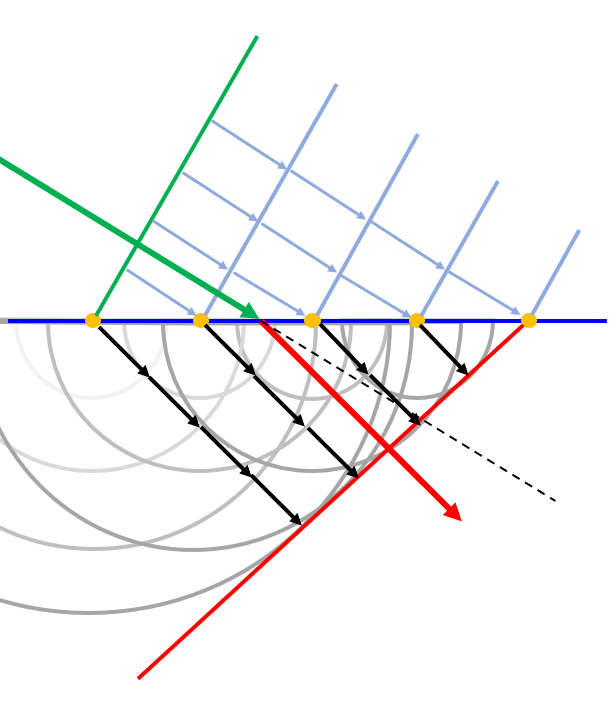
Esto se denomina la refracción de la luz.
ID:(12670, 0)
Relación de angulo entre haz incidente y haz transmitido
Gleichung 
Del principio de Huygens se puede establecer la relación entre los ángulos de incidencia y el de transmisión:
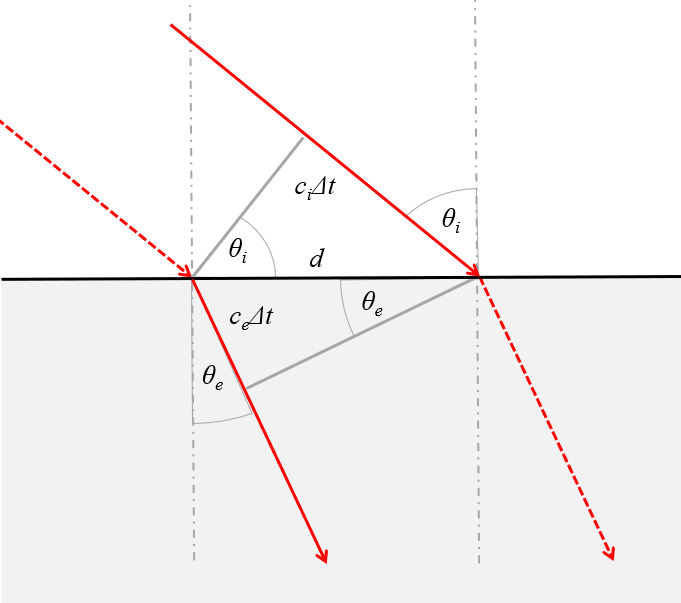
Se ve claramente que la diferencia se da justamente por el efecto de la variación de la velocidad de la luz en cada medio.
ID:(12672, 0)
Brechung der Lichtstrahl von Vakuum zu Medium
Variable 
Paso de medio con mayor a menor velocidad

ID:(1849, 0)
Brechung der Lichtstrahl von Medium zu Vakuum
Audio 
Cuando un haz pasa de un medio de menor velocidad

ID:(1850, 0)
Medición de la ley de Snell
Video 
Para confirmar empiricamente la ley de Snell se usa un banco optico:
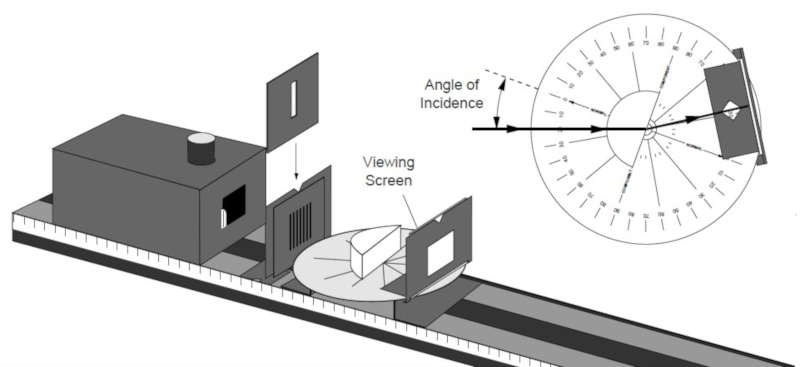
Los banco ópticos son barras largas en que se pueden montar
• fuentes de luz
• colimadores (placas con rendijas)
• espejos planos y curvos
• prismas y lentes
ID:(12671, 0)
Medición del haz refractado
Einheit 
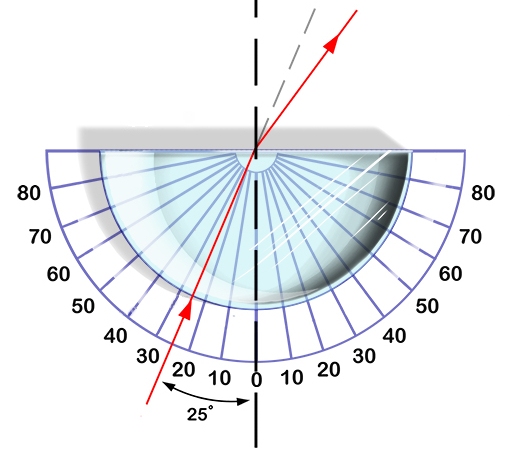
Para mostrar/estudiar la refracción se usa un vidrio que por un lado es curvo. Esto permite girar el vidrio sin que su superficie deje de estar perpendicular al haz por lo que ingresa sin refracción. De esta forma se puede ver como el haz se refracta en la interface vidrio-aire:

ID:(12673, 0)
Snells Gesetz
Beschreibung 
Das Snellsche Gesetz ermöglicht es, den Winkel zu bestimmen, mit dem ein Lichtstrahl gebrochen (abgelenkt) wird, basierend auf den Eigenschaften beider Medien. Die Eigenschaften beider Mittel beziehen sich auf den Brechungsindex oder die Ausbreitungsgeschwindigkeit im jeweiligen Medium.
Variablen
Berechnungen
Berechnungen
Gleichungen
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
| $\displaystyle\frac{ \sin \theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
(ID 3342)
Como la relaci n entre los ngulos de incidencia y refracci n es
| $\displaystyle\frac{ \sin \theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
y el indice de refracci n se define como
| $ n =\displaystyle\frac{ c }{ v }$ |
\\n\\nse tiene que con\\n\\n
$n_i=\displaystyle\frac{c}{c_i}$
y\\n\\n
$n_e=\displaystyle\frac{c}{c_e}$
\\n\\nque\\n\\n
$\displaystyle\frac{c_i}{c_e}=\displaystyle\frac{c_i}{c}\displaystyle\frac{c}{c_e}=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{\sin\theta_i}{\sin\theta_e}$
por lo que resulta
| $ n_i \sin \theta_i = n_e \sin \theta_r $ |
(ID 3343)
Die Energie einer Welle oder eines Teilchens (Photon) des Lichts wird durch
| $ \epsilon = h \nu $ |
ausgedr ckt. Wenn diese Energie von einem Medium, zum Beispiel einem Vakuum mit der Lichtgeschwindigkeit $c$, in ein anderes Medium mit der Lichtgeschwindigkeit $c_m$ bergeht, folgt daraus, dass die Frequenz des Lichts unver ndert bleibt. Allerdings bedeutet dies, dass sich die Wellenl nge ndern muss, da die Lichtgeschwindigkeit gleich dem Produkt aus Frequenz und Wellenl nge ist, wie in der Gleichung
| $ c = \nu \lambda $ |
ausgedr ckt wird.
Daher kann, wenn wir eine Wellenl nge des Lichts in einem Medium $\lambda_m$ und im Vakuum $\lambda$ betrachten, der Brechungsindex definiert werden als
| $ n =\displaystyle\frac{ c }{ v }$ |
und kann wie folgt ausgedr ckt werden:
$n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}$
Mit anderen Worten,
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
(ID 9776)
Beispiele
Cuando la luz en un medio con velocidad de la luz
La transmisi n sin embargo no solo puede perder intensidad, por la fracci n reflejada, tambi n puede ser desviada. Este desv o se denomina refracci n.
(ID 429)
Para aplicar el principio de Huygens en el caso del paso de luz de un medio a un segundo en que la velocidad de la luz varia, se debe considerar fuentes que gatillada en el primero y genera ondas esf ricas en el segundo:

(ID 12667)
Wenn $n$ der Brechungsindex in einem Medium ist und $\lambda$ die Wellenl nge im Vakuum ist, wird die Wellenl nge $\lambda_m$ beim Propagieren im Medium sein
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
(ID 9776)
A medida que se crea la segunda fuente la primera ya ha irradiado:

Eso si se debe tener presente que al ser las velocidades distintas el tama o de la radiaci n esf rica es de diferente tama o en los dos medios.
(ID 12668)
Continuando se va viendo como se comienza a generar un nuevo frente de onda que no presenta la misma orientaci n que el primero:

(ID 12669)
Finalmente se pueden dibujar los frentes de onda quedando claro que la direcci n de propagaci n ha cambiado:

Esto se denomina la refracci n de la luz.
(ID 12670)
Del principio de Huygens se puede establecer la relaci n entre los ngulos de incidencia y el de transmisi n:

Se ve claramente que la diferencia se da justamente por el efecto de la variaci n de la velocidad de la luz en cada medio.
(ID 12672)
La relaci n entre los ngulos de incidencia y refractados indicados en la siguiente gr fica

se pueden escribir en funci n de la velocidad de la luz en cada medio
| $\displaystyle\frac{ \sin \theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
(ID 3342)
La ley de Snell para el paso de la luz de un medio de indice
| $ n_i \sin \theta_i = n_e \sin \theta_r $ |
(ID 3343)
Der Brechungsindex, dargestellt als $n$, wird als das Verh ltnis der Lichtgeschwindigkeit im Vakuum, dargestellt als $c$, zur Lichtgeschwindigkeit im Medium, dargestellt als $c_m$, definiert:
| $ n =\displaystyle\frac{ c }{ v }$ |
(ID 3192)
Paso de la luz por un objeto
(ID 1853)
Paso de medio con mayor a menor velocidad

(ID 1849)
Cuando un haz pasa de un medio de menor velocidad

(ID 1850)
Para confirmar empiricamente la ley de Snell se usa un banco optico:

Los banco pticos son barras largas en que se pueden montar
• fuentes de luz
• colimadores (placas con rendijas)
• espejos planos y curvos
• prismas y lentes
(ID 12671)
Para mostrar/estudiar la refracci n se usa un vidrio que por un lado es curvo. Esto permite girar el vidrio sin que su superficie deje de estar perpendicular al haz por lo que ingresa sin refracci n. De esta forma se puede ver como el haz se refracta en la interface vidrio-aire:

(ID 12673)
ID:(302, 0)
