User:
Flat Mirror
Storyboard 
In the case of a flat mirror, the light is reflected at an angle identical to the one it affected.
In general, the light does not have the information that has been reflected with what the eye assumes that the light originates 'behind' the mirror.
ID:(1263, 0)
La ley de reflexión
Definition
Aplicando el principio de Huygens se muestra que un haz que incide sobre una superficie se refleja bajo un angulo igual al de incidencia:
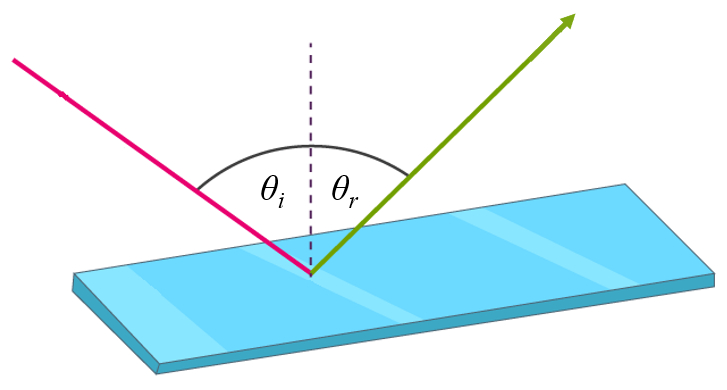
ID:(12758, 0)
A Mirror
Image
A mirror looks like a window to another room. The effect is created by the reflected light that the eye assumes was not reflected but comes from an object behind the mirror.
ID:(9777, 0)
Relación entre ángulos de incidencia y reflexión
Note
En caso de dos espejos con una esquina
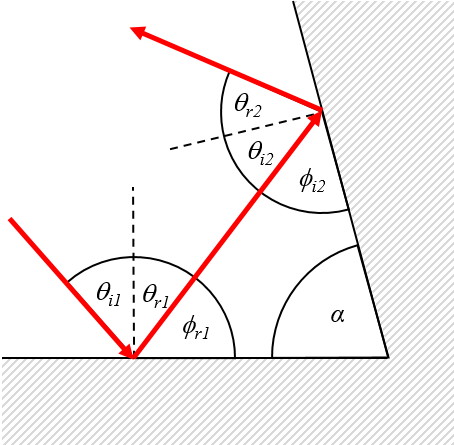
se pueden calcular los ángulos con la relación de reflexión
| $ \theta_i = \theta_r $ |
el calculo del complemento del angulo incidente
| $ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $ |
el calculo del complemento del angulo de reflección
| $ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $ |
y la relación entre los ángulos de un triangulo
| $ \pi = \alpha + \beta + \gamma $ |
ID:(12666, 0)
Relación entre ángulos de incidencia y reflexión
Quote
Del análisis mediante el principio de Huygens se concluye que los ángulos de incidencia y reflexión son iguales:
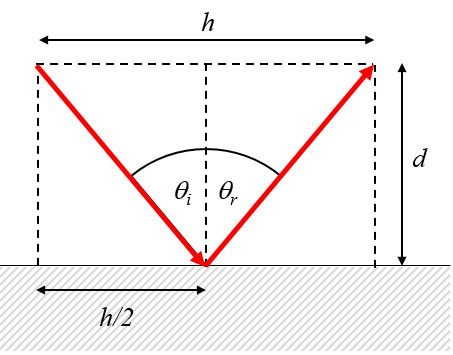
ID:(12665, 0)
Flat Mirror
Description
In the case of a flat mirror, the light is reflected at an angle identical to the one it affected. In general, the light does not have the information that has been reflected with what the eye assumes that the light originates 'behind' the mirror.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Como la suma de los ngulos internos en un triangulo es
| $ \pi = \alpha + \beta + \gamma $ |
se tiene que en un rect ngulo, en el que uno de los ngulos es
| $ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $ |
(ID 10925)
Como la suma de los ngulos internos en un triangulo es
| $ \pi = \alpha + \beta + \gamma $ |
se tiene que en un rect ngulo, en el que uno de los ngulos es
| $ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $ |
(ID 10928)
Examples
(ID 16066)
Aplicando el principio de Huygens se muestra que un haz que incide sobre una superficie se refleja bajo un angulo igual al de incidencia:
(ID 12758)
A mirror looks like a window to another room. The effect is created by the reflected light that the eye assumes was not reflected but comes from an object behind the mirror.
(ID 9777)
Del an lisis mediante el principio de Huygens se concluye que los ngulos de incidencia y reflexi n son iguales:
(ID 12665)
En caso de dos espejos con una esquina
se pueden calcular los ngulos con la relaci n de reflexi n
| $ \theta_i = \theta_r $ |
el calculo del complemento del angulo incidente
| $ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $ |
el calculo del complemento del angulo de reflecci n
| $ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $ |
y la relaci n entre los ngulos de un triangulo
| $ \pi = \alpha + \beta + \gamma $ |
(ID 12666)
(ID 16061)
Para la luz reflejada el angulo del haz respecto de la normal
| $ \theta_i = \theta_r $ |
(ID 3262)
Para el calculo de los ngulos en el caso de que los haces se reflejan en un espejo es til poder calcular el angulo complementario al de incidencia. Por ello se tiene que
| $ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $ |
(ID 10928)
Para el calculo de los ngulos en el caso de que los haces se reflejan en un espejo es til poder calcular el angulo complementario al de reflexi n. Por ello se tiene que
| $ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $ |
(ID 10925)
| $ \pi = \alpha + \beta + \gamma $ |
(ID 10926)
El angulo de incidencia
| $ \tan \theta_i =\displaystyle\frac{ h }{2 d }$ |
(ID 9779)
ID:(1263, 0)