Usuario:
Flujo Radiante
Storyboard 
La luz es irradiada, es decir fluye por lo que las magnitudes fundamentales se refieren a la cantidad de fotones que son emitidos, atraviesan una sección o son absorbidos.
Como la cantidad de fotones de un color es proporcional a la energía el flujo es proporcional a la energía por tiempo o sea la potencia.
ID:(297, 0)
Decrecimiento de intensidad con la distancia
Definición
Si pensamos en la luz como un flujo de fotones, estos se alejarán de su fuente y se distribuirán cada vez sobre una superficie mayor:
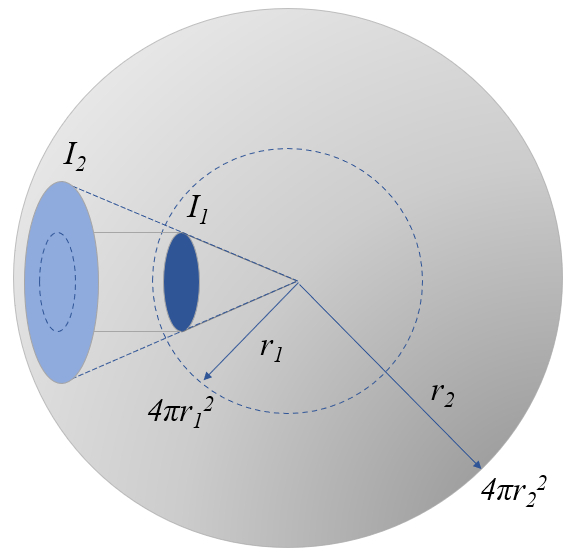
De esta manera, la intensidad disminuye a medida que nos alejamos de la fuente, disminuyendo inversamente al cuadrado de la distancia.
ID:(1664, 0)
Intensidad de Luz por Orificio
Imagen
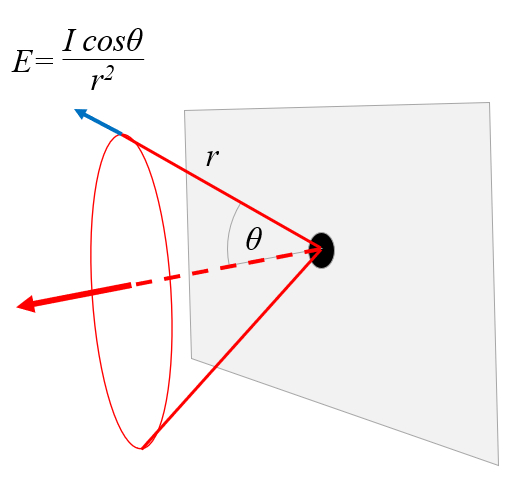
Cuando la luz pasa a través del orificio, la intensidad depende del ángulo del haz con respecto a la dirección original del haz, representado por $\theta$.
La intensidad $I$ está definida como
 $I(r,\theta)=\displaystyle\frac{r_0^2}{r^2}I_0\cos\theta$
|
ID:(3352, 0)
Luz a través de una rendija
Nota
Cuando la luz pasa a través de un orificio, comienza a dispersarse. Su intensidad disminuye tanto con la distancia al orificio como con el ángulo con respecto a la dirección original de propagación:
ID:(1861, 0)
Flujo Radiante
Descripción
La luz es irradiada, es decir fluye por lo que las magnitudes fundamentales se refieren a la cantidad de fotones que son emitidos, atraviesan una sección o son absorbidos. Como la cantidad de fotones de un color es proporcional a la energía el flujo es proporcional a la energía por tiempo o sea la potencia.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
Si pensamos en la luz como un flujo de fotones, estos se alejar n de su fuente y se distribuir n cada vez sobre una superficie mayor:
De esta manera, la intensidad disminuye a medida que nos alejamos de la fuente, disminuyendo inversamente al cuadrado de la distancia.
(ID 1664)
Cuando la luz pasa a trav s del orificio, la intensidad depende del ngulo del haz con respecto a la direcci n original del haz, representado por $\theta$.
La intensidad $I$ est definida como
| $I(r,\theta)=\displaystyle\frac{r_0^2}{r^2}I_0\cos\theta$ |
(ID 3352)
Cuando la luz pasa a trav s de un orificio, comienza a dispersarse. Su intensidad disminuye tanto con la distancia al orificio como con el ngulo con respecto a la direcci n original de propagaci n:
(ID 1861)
Dado que los fotones se distribuyen sobre una superficie de tama o $4\pi r^2$, la cantidad de fotones por unidad de superficie disminuye. Esto significa que la densidad, que representa el n mero de fotones por unidad de rea, se reduce de acuerdo con la relaci n:
| $ I_r =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0 $ |
La intensidad se mide en candelas (cd), que corresponden a la cantidad de luz que emite un objeto a una temperatura de $2042.5 K$ sobre una superficie de tama o $1/600000 m^2$.
(ID 3191)
ID:(297, 0)