Benützer:
Geometrie der Strahlen auf einem Objektiv
Definition 
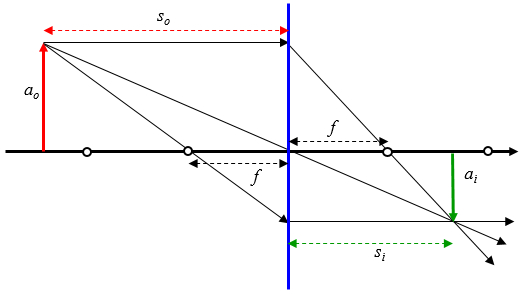
Bei einer Bikonvexlinse ein Strahl, der auf die Linse trifft
- Parallel zur optischen Achse wird durch den Fokus gebrochen
- über den Fokus wird parallel zur optischen Achse gebrochen
- über den Ursprung der durchgehenden optischen Achse in einer geraden Linie
Was im Fall eines Objekts in einer Entfernung größer als das Foto entspricht:
ID:(1856, 0)
Similitud tamaños y posiciones
Bild
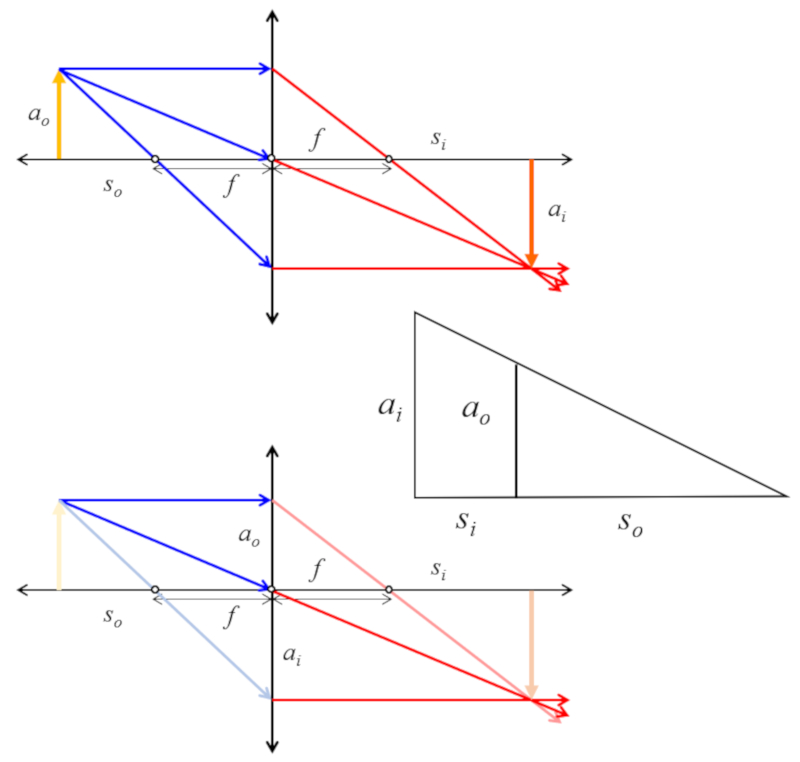
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones
ID:(12697, 0)
Similitud tamaños, posición de objeto y foco
Notiz
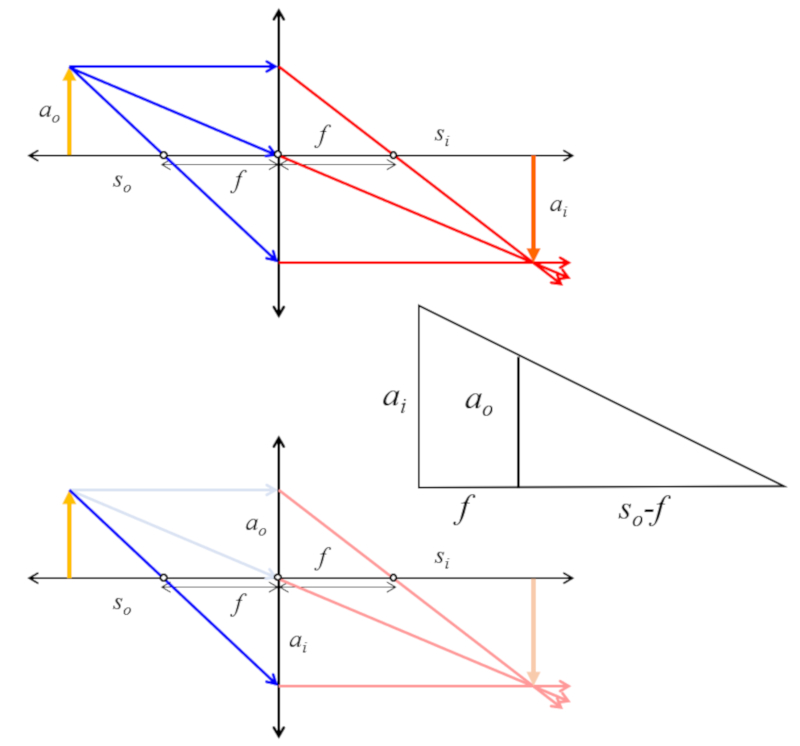
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:
ID:(12698, 0)
Posición de la imagen
Zitat
Como la relación entre el foco, posición del objeto y posición de la imagen esta dada por\\n\\n
$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$
\\n\\ny se introduce las variables\\n\\n
$x=\displaystyle\frac{s_o}{f}$
, y\\n\\n
$y=\displaystyle\frac{s_i}{f}$
\\n\\nse puede escribir la relación\\n\\n
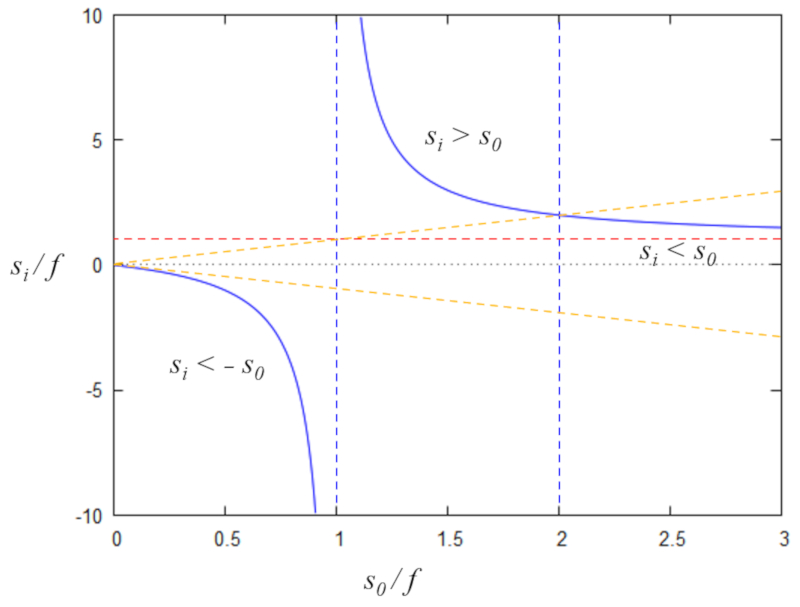
$y=\displaystyle\frac{x}{x-1}$
que se grafica como
ID:(12699, 0)
Tamaño de la imagen
Übung
Como la relación de los tamaño de la imagen se puede escribir como\\n\\n
$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{s_i}{s_o}$
\\n\\nCon la relación entre las posiciones\\n\\n
$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$
\\n\\nla relación de tamaños se puede escribir como\\n\\n
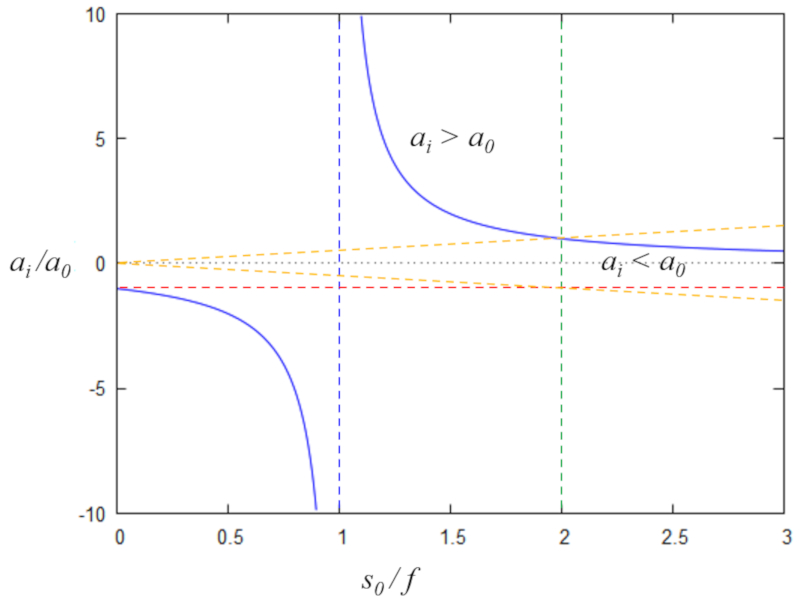
$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{1}{1-s_o/f}$
\\n\\npor lo que con\\n\\n
$x=\displaystyle\frac{s_o}{f}$
, y\\n\\n
$y=\displaystyle\frac{a_i}{a_o}$
\\n\\nse puede escribir la relación\\n\\n
$y=\displaystyle\frac{1}{x-1}$
que se grafica como
ID:(12700, 0)
Optische Elemente
Beschreibung
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Una relaci n se puede armar con los tri ngulos del lado del objeto. En este caso la similitud nos permite escribir que el tama o del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relaci n de similitud de los tri ngulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
(ID 3347)
Beispiele
Bei einer Bikonvexlinse ein Strahl, der auf die Linse trifft
- Parallel zur optischen Achse wird durch den Fokus gebrochen
- ber den Fokus wird parallel zur optischen Achse gebrochen
- ber den Ursprung der durchgehenden optischen Achse in einer geraden Linie
Was im Fall eines Objekts in einer Entfernung gr er als das Foto entspricht:
(ID 1856)
Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os con posiciones
(ID 12697)
F r jedes Objektiv k nnen Sie charakteristische Strahlen zeichnen, mit denen Sie auf hnliche Weise zeigen k nnen, dass die Gr en des Objekts und des Bildes im gleichen Verh ltnis stehen wie ihre Abst nde zum optischen Element (Objektiv oder Spiegel).
Wenn das Objekt eine Gr e
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
(ID 3346)
Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os, posici n del objeto y foco:
(ID 12698)
Por similitud de los tri ngulos de los tama os del objeto y la imagen y las posiciones del objeto y foco permite por similitud de tri ngulos mostrar que:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
(ID 3347)
Como la relaci n entre el foco, posici n del objeto y posici n de la imagen esta dada por\\n\\n
$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$
\\n\\ny se introduce las variables\\n\\n
$x=\displaystyle\frac{s_o}{f}$
, y\\n\\n
$y=\displaystyle\frac{s_i}{f}$
\\n\\nse puede escribir la relaci n\\n\\n
$y=\displaystyle\frac{x}{x-1}$
que se grafica como
(ID 12699)
Como la relaci n de los tama o de la imagen se puede escribir como\\n\\n
$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{s_i}{s_o}$
\\n\\nCon la relaci n entre las posiciones\\n\\n
$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$
\\n\\nla relaci n de tama os se puede escribir como\\n\\n
$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{1}{1-s_o/f}$
\\n\\npor lo que con\\n\\n
$x=\displaystyle\frac{s_o}{f}$
, y\\n\\n
$y=\displaystyle\frac{a_i}{a_o}$
\\n\\nse puede escribir la relaci n\\n\\n
$y=\displaystyle\frac{1}{x-1}$
que se grafica como
(ID 12700)
ID:(1667, 0)