User:
Particles in Magnetic Fields
Storyboard 
Electric charges moving in a magnetic field are deflected perpendicular to the direction in which they move and in which the magnetic field points.
The force acting on the particle depends on the charge, the velocity and the magnetic field is called the Lorentz force.
ID:(818, 0)
Parallel currents
Definition
When two currents are allowed to flow in a parallel manner, we observe an attractive force between the wires.
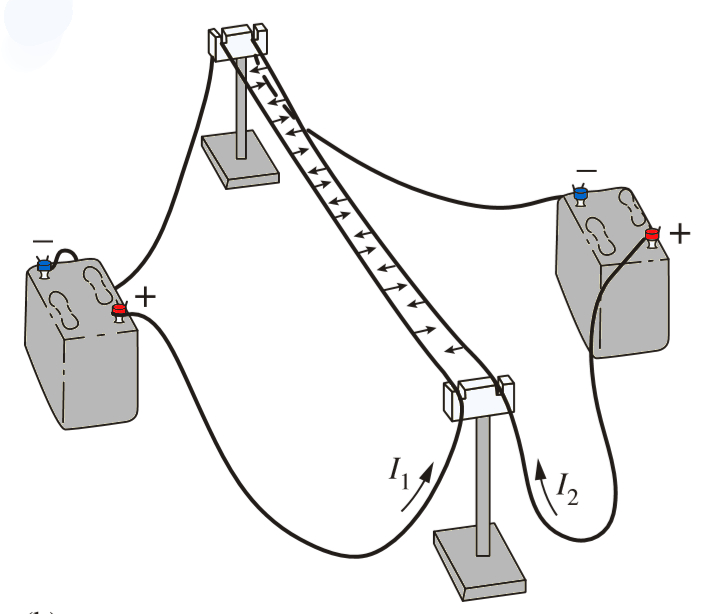
It's worth recalling that currents consist of electrons in motion, and electrons naturally repel each other due to their negative charges. However, when these charges are in motion, this repulsive force turns into an attractive force, resulting in the observed attraction between the negatively charged conductors.
ID:(11772, 0)
Opposite parallel currents
Image
When two currents are allowed to flow in a parallel but opposite direction, we observe a repulsive force between the wires.
Comparing this experiment to the one where the flow is parallel but in the same direction, the key difference lies in the presence of relative velocity in the latter case.
ID:(11773, 0)
Parallel currents, field is not electric
Note
If a metal plate is placed between both conductors, no noticeable effect is observed:
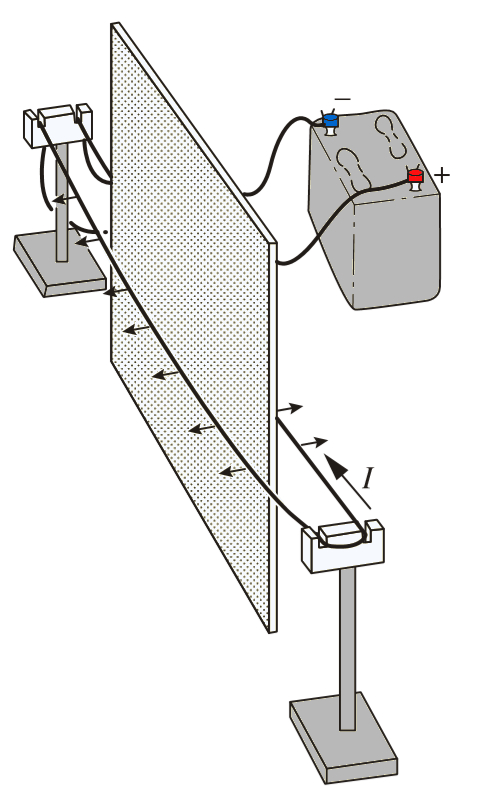
Hence, we conclude that the generated field does not correspond to a traditional electric field.
ID:(11774, 0)
Current effect on a compass
Quote
When a compass is exposed to an electric current, the following observations can be made:
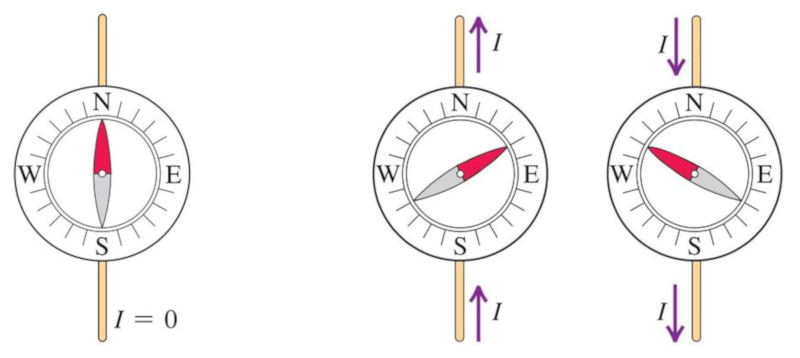
In summary, the compass needle:
• does not rotate if there is no electric current present
• rotates when there is a flow of electric current
• if the direction of the current flow is reversed, the rotation of the needle also reverses.
ID:(11775, 0)
Detection of the generated magnetic field
Exercise
When you explore the space around a wire with a compass, you'll notice that the current induces the presence of a magnetic field:
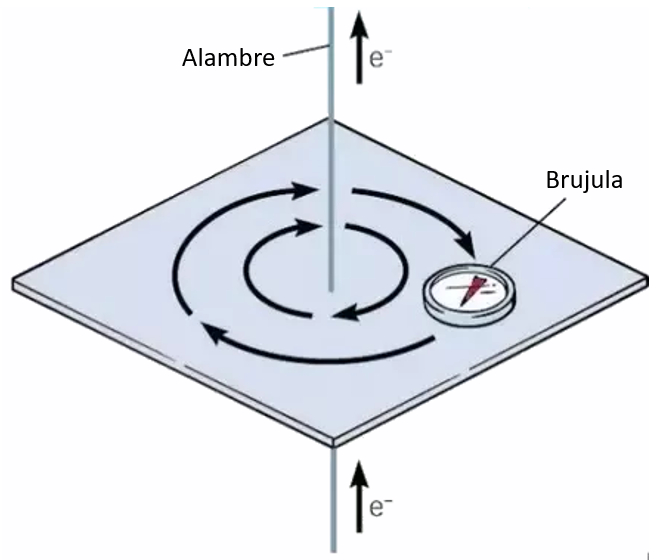
This is why parallel wires can either attract or repel each other depending on the direction of the current. The key insight here is that:
Current generates a magnetic field, and this magnetic field exerts a force on moving charges.
ID:(11776, 0)
Particles in Magnetic Fields
Storyboard
Electric charges moving in a magnetic field are deflected perpendicular to the direction in which they move and in which the magnetic field points. The force acting on the particle depends on the charge, the velocity and the magnetic field is called the Lorentz force.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
The force ($F$), which generates the magnetic flux density ($B$) on the charge ($q$), moving under a angle between speed and magnetic field ($\theta$) with the speed ($v$), is expressed as:
La ecuaci n de movimiento se deriva del equilibrio entre la fuerza generada por the magnetic flux density ($B$) actuando sobre the charge ($q$) y the particle mass ($m$), que se desplaza con the particle speed ($v$) a the radius ($r$). Esto se expresa mediante la siguiente relaci n:
The orbit at a radius of gyration of particle in magnetic field ($r$) depends on the particle mass ($m$), the speed ($v$), the charge ($Q$), and the magnetic flux density ($B$), and is described by the following relationship:
The angular Speed ($\omega$) is derived from the charge ($q$), the magnetic flux density ($B$), and the particle mass ($m$), using the following relationship:
ID:(818, 0)