User:
Ferromagnet or solenoid
Definition 
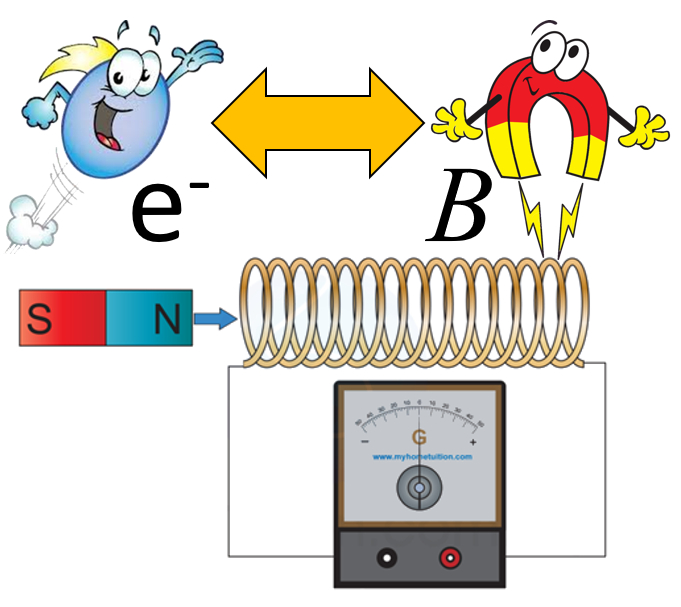
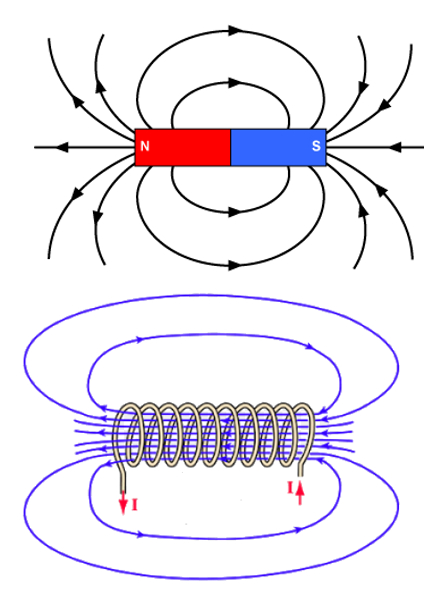
When current is allowed to flow through a solenoid, we observe that it creates a magnetic field similar to that of a magnetized bar. This indicates that the flow of electrons is capable of generating magnetic fields, and these fields are equivalent to permanent magnetic fields.
ID:(12116, 0)
Lenz's law
Quote
Al igual que en la mecánica en que la inercia trata de resistirse al cambio de estado en la electrodinámica existe un fenómeno análogo que fue descrito inicialmente por Lenz. Este se observa en particular en la inducción magnética en que las corrientes generadas son siempre de modo de oponerse al imán que las esta generando. En otras palabras las corrientes generadas crean un campo magnético que esta en oposición al que las origina inicialmente. Esto es lo que se denomina la ley de Lenz.
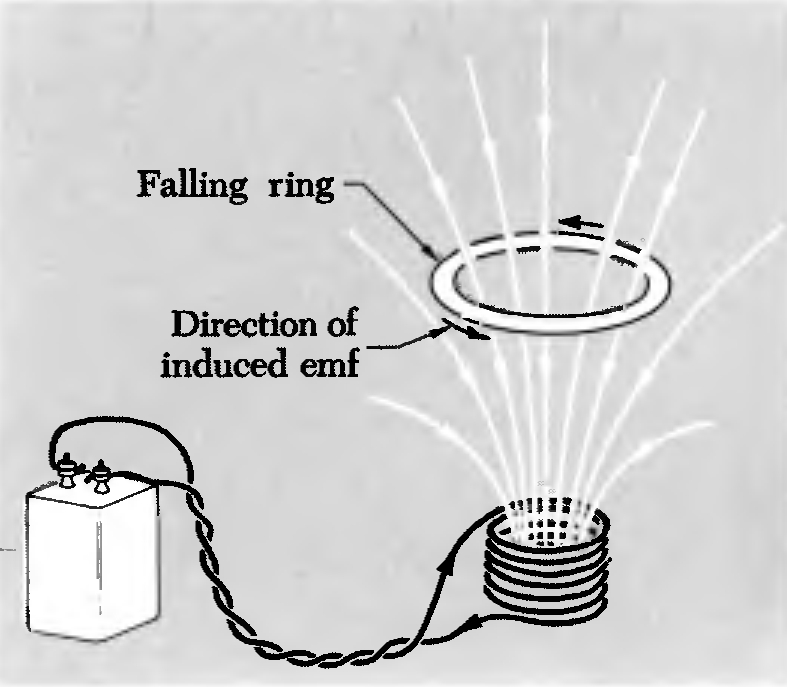
Ejemplo de la aplicación de la ley de Lenz: si se deja caer un anillo sobre un campo magnético se genera en el una corriente tal que genera un campo de polaridad opuesta que se resiste a caer sobre el campo existente.
ID:(12174, 0)
Calculation of a magnetic field
Exercise
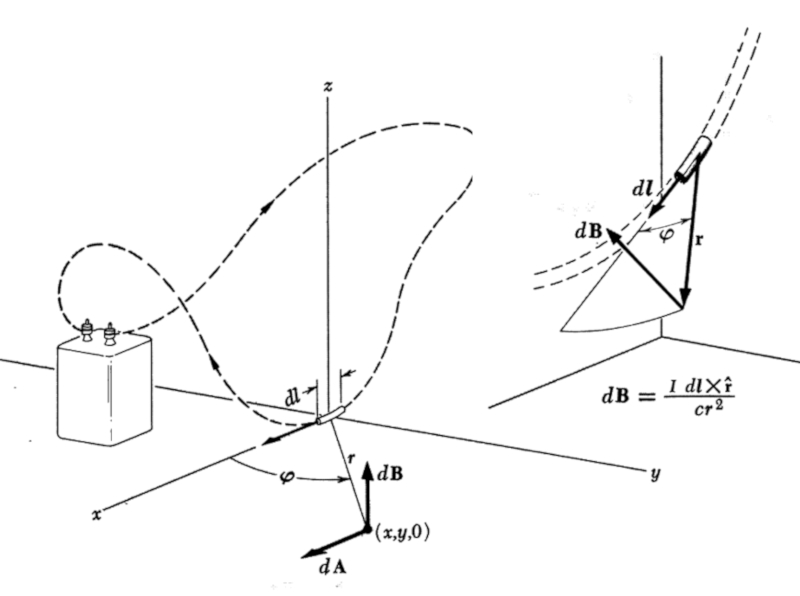
A magnetic field is constructed based on the collective contributions of all elements conducting electricity. When we consider one of these particular elements, it can be observed how it participates in the magnetic field, as depicted in the image:
ID:(12179, 0)
Faraday's law and magnetic field
Storyboard
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
When current is allowed to flow through a solenoid, we observe that it creates a magnetic field similar to that of a magnetized bar. This indicates that the flow of electrons is capable of generating magnetic fields, and these fields are equivalent to permanent magnetic fields.
The magnetic component of the Lorentz force is described by the following equation:
This can be expressed as:
El campo y flujo magn tico son proporcionales, por lo que se tiene con
Similar to the electric field flux, we can introduce magnetic flux $\Phi$. If we introduce a magnetic flux density $B$, we can define the flux as:
Faraday observo que la variaci n temporal del flujo magn tico inducia una diferencia de potencial que, de conectarse a un alambre, puede generar una corriente. Esta relaci n se puede escribir con
El potencial creado se denomina tambi n 'fuerza electromotriz' (fem) pues es el mecanismo con el que se genera la fuerza que mueve un motor.
La ley de Faraday que establece con
Para el caso que se trabaja con valores medios se puede estimar que la variaci n del flujo magn tico es con
Al igual que en la mec nica en que la inercia trata de resistirse al cambio de estado en la electrodin mica existe un fen meno an logo que fue descrito inicialmente por Lenz. Este se observa en particular en la inducci n magn tica en que las corrientes generadas son siempre de modo de oponerse al im n que las esta generando. En otras palabras las corrientes generadas crean un campo magn tico que esta en oposici n al que las origina inicialmente. Esto es lo que se denomina la ley de Lenz.
Ejemplo de la aplicaci n de la ley de Lenz: si se deja caer un anillo sobre un campo magn tico se genera en el una corriente tal que genera un campo de polaridad opuesta que se resiste a caer sobre el campo existente.
A simple example of flux variation can be estimated using the formula:
Assuming that the magnetic flux density is constant across the section, represented by:
In such a case, when a conductor is withdrawn from a magnetic field, the section of the conductor reduces as it moves. If we simplify the calculations by considering a rectangular shape, we can express it as:
$\displaystyle\frac{\Delta\Phi}{\Delta t} = B L \displaystyle\frac{\Delta s}{\Delta t}=B L v$
Here, the change in path over time is defined as velocity. Therefore, we can estimate that:
A magnetic field is constructed based on the collective contributions of all elements conducting electricity. When we consider one of these particular elements, it can be observed how it participates in the magnetic field, as depicted in the image:
En general para el calculo de campos magn ticos se puede usar la llamada ley de Biot Savat que para una corriente dada en un segmento de alambre calcula su contribuci n a un campo magn tico en un punto del espacio. Con
ID:(1626, 0)