Potencial eléctrico
Storyboard 
Cada vez que se introduce el concepto de fuerza, y por ende el de energía, es posible modelar la fuerza utilizando una energía potencial. Del mismo modo, para la fuerza descrita por la ley de Coulomb, se puede derivar una energía potencial conocida en este contexto como potencial eléctrico.
ID:(1561, 0)
Potencial eléctrico
Storyboard 
Cada vez que se introduce el concepto de fuerza, y por ende el de energía, es posible modelar la fuerza utilizando una energía potencial. Del mismo modo, para la fuerza descrita por la ley de Coulomb, se puede derivar una energía potencial conocida en este contexto como potencial eléctrico.
Variables
Cálculos
Cálculos
Ecuaciones
La diferencia de potencial ($\Delta\varphi$) es igual a la suma de el campo eléctrico ($\vec{E}$) a lo largo de un camino integrado sobre el elemento de camino recorrido ($d\vec{s}$):
Como la diferencia de potencial ($\Delta\varphi$) se calcula considerando el potencial eléctrico ($\varphi$) menos el potencial eléctrico base ($\varphi_0$):
por lo que
Dado que la variación infinitesimal del trabajo ($dW$) est relacionado con la fuerza ($\vec{F}$) y el elemento de camino recorrido ($d\vec{s}$) por:
y la fuerza se puede expresar en funci n de el campo eléctrico ($\vec{E}$) y la carga de prueba ($q$) como:
se puede calcular la energ a asociada al campo el ctrico utilizando:
La variación infinitesimal del potencial ($d\varphi$) es la variación infinitesimal del trabajo ($dW$) por la carga de prueba ($q$):
Por lo tanto, con el campo eléctrico ($\vec{E}$) y el elemento de camino recorrido ($d\vec{s}$):
Esto resulta en:
La unidad en que se mide el potencial el ctrico es el Newton metro por Coulomb (N m/C o J/C), que se denomina Voltio.
Si se suman las contribuciones de la variación infinitesimal del potencial ($d\varphi$) con el campo eléctrico ($\vec{E}$) por un elemento de camino recorrido ($d\vec{s}$):
Se obtiene por un lado la diferencia de potencial ($d\varphi$):
$d\varphi_1+d\varphi_2+d\varphi_3+\ldots = \displaystyle\sum_i d\varphi_i = \Delta\varphi$
y la suma de los campos a lo largo de caminos:
$\vec{E}_1\cdot d\vec{s}_1+\vec{E}_2\cdot d\vec{s}_2+\vec{E}_3\cdot d\vec{s}_3+\ldots = \displaystyle\sum_i \vec{E}_i \cdot d\vec{s}_i$
que en el l mite continuo puede escribirse como la integral de:
Al calcular la integral de el campo eléctrico ($E$) sobre un camino cerrado el elemento de camino recorrido ($d\vec{s}$), se puede descomponer la integral en dos partes: una desde P1 a P2 y otra de regreso de P2 a P1. De esta forma, se obtiene que
$\displaystyle\oint_C \vec{E}\cdot d\vec{s} = \displaystyle\oint_{P1}^{P2} \vec{E}\cdot d\vec{s} - \displaystyle\oint_{P2}^{P1} \vec{E}\cdot d\vec{s} = 0$
por lo que, con
Por ello,
Si una part cula cargada recorre un camino cerrado en un campo el ctrico, el campo aportar la misma cantidad de energ a que le requerir a la part cula para completar el camino.
Como la variación infinitesimal del potencial ($d\varphi$) resulta del producto de el campo eléctrico ($\vec{E}$) con el elemento de camino recorrido ($d\vec{s}$)
y considerando las componentes de el campo eléctrico ($\vec{E}$)
$\vec{E} = \hat{x} E_x + \hat{y} E_y + \hat{z} E_z$
junto con las de el elemento de camino recorrido ($d\vec{s}$)
$d\vec{s} = \hat{x} dx + \hat{y} dy + \hat{z} dz$
la expresi n se simplifica a
$d\varphi = -E_x dx - E_y dy - E_z dz$
Con la variaci n del potencial
y el gradiente calculado como
se deduce que el gradiente del potencial es igual al negativo del campo el ctrico.
Ejemplos
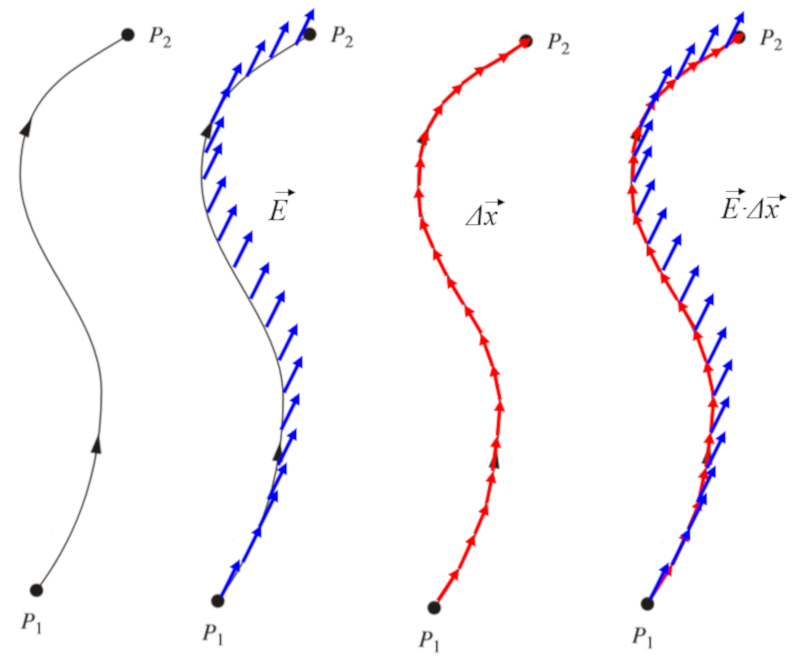
Si se consideran m ltiples ERROR:5480,0 a lo largo de un camino, es posible calcular la energ a por carga, correspondiente a el potencial eléctrico ($\varphi$), necesaria para mover una carga a lo largo de dicho camino con una fuerza por carga que corresponde a el campo eléctrico ($\vec{E}$):
Esto se representa gr ficamente como:
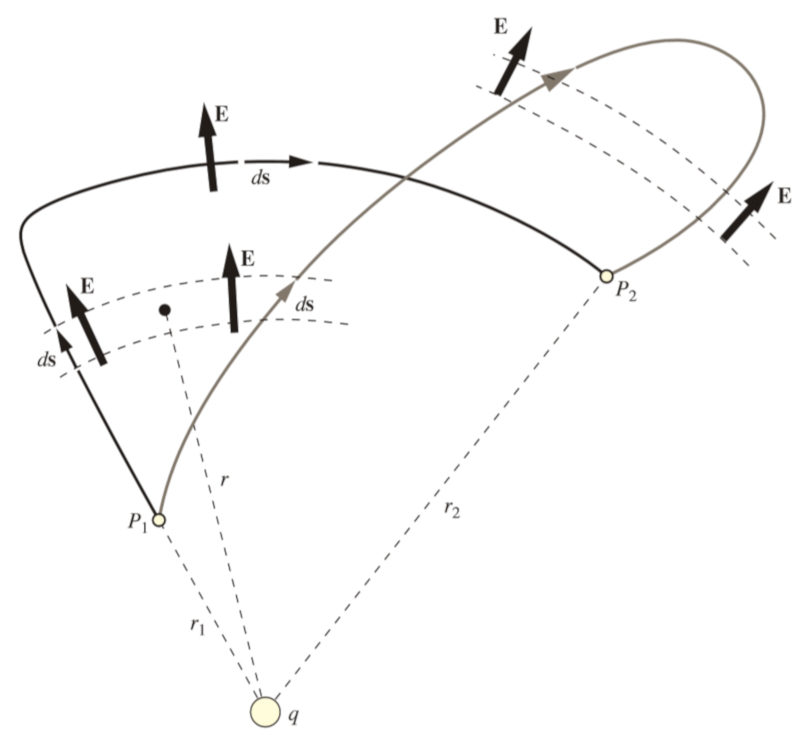
Si consideramos dos caminos distintos,
• uno en el que se llega a una cierta distancia de la carga y luego se aproxima a ella de forma perpendicular al campo el ctrico,
• otro en el que se aleja m s del origen y luego regresa hacia la carga, compensando mediante el signo el monto adicional recorrido,
se observar que ambos caminos producen el mismo resultado:
Por lo tanto, podemos concluir que
El potencial el ctrico entre dos puntos es igual al integral de l nea del campo el ctrico a lo largo de un segmento, siendo esta integral independiente del camino elegido.
Con este conocimiento, es posible proceder a estimar campos el ctricos seleccionando el camino m s sencillo para la integraci n o suma de campos por segmentos.
La variación infinitesimal del trabajo ($dW$) es con el campo eléctrico ($\vec{E}$), la carga de prueba ($q$) y el elemento de camino recorrido ($d\vec{s}$) es igual a
En el contexto de la energ a para una carga la carga de prueba ($q$), surge nuevamente la problem tica de un par metro que, al ser medido, depende del instrumental de medici n. Por ello, tiene sentido definir una energ a por unidad de carga. As se introduce la variación infinitesimal del potencial ($d\varphi$) como la variación infinitesimal del trabajo ($dW$) por la carga de prueba ($q$):
Se incluye un signo negativo porque se entiende que es la energ a que se consume, es decir, se resta del sistema.
La variación infinitesimal del potencial ($d\varphi$) es con el campo eléctrico ($\vec{E}$) y el elemento de camino recorrido ($d\vec{s}$) igual
La diferencia de potencial ($\Delta\varphi$) es igual a la suma de el campo eléctrico ($\vec{E}$) a lo largo de un camino integrado sobre el elemento de camino recorrido ($d\vec{s}$):
La diferencia de potencial ($\Delta\varphi$) se calcula considerando el potencial eléctrico ($\varphi$) menos el potencial eléctrico base ($\varphi_0$):
El potencial eléctrico ($\varphi$) se puede calcular de el potencial eléctrico base ($\varphi_0$) y el campo eléctrico ($\vec{E}$) integrado a lo largo de un camino sobre el elemento de camino recorrido ($d\vec{s}$):
La integral del producto de el campo eléctrico ($E$) multiplicado en la direcci n del camino, es decir, integrado sobre el elemento de camino recorrido ($d\vec{s}$) a lo largo de un camino cerrado, es nula:
El campo eléctrico ($\vec{E}$) es igual a menos del gradiente de el potencial eléctrico ($\varphi$):
ID:(1561, 0)