Utilizador:
Campo elétrico
Storyboard 
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
La força ($\vec{F}$) em la carga de teste ($q$) em la posição ($\vec{r}$) depender de o número de cobranças ($N$), indexado por $i$ e representado por la carga iônica i ($Q_i$) localizado em la posição de uma carga i ($\vec{u}_i$). Com os par metros la constante dielétrica ($\epsilon$) e la constante de campo elétrico ($\epsilon_0$), isso pode ser escrito da seguinte maneira:
Com a defini o de o campo elétrico ($\vec{E}$) dada por
segue que o campo el trico de uma distribui o de cargas
A magnitude de la força com massa constante ($F$) gerada entre duas cargas, representadas por la carga de teste ($q$) e la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada utilizando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte forma:
Usando a defini o do campo el trico como
obt m-se
Exemplos
Para medir a for a de Coulomb, necess rio introduzir uma carga de teste no sistema. Se essa carga de teste for la carga de teste ($q$), pode-se estimar a for a por unidade de carga que as cargas do sistema exercem sobre a carga de teste. A magnitude da for a la força ($\vec{F}$) por unidade de carga la carga de teste ($q$) chamada de campo el trico o campo elétrico ($\vec{E}$) e medida em Newtons (N) por Coulomb (C). O campo el trico medido assumindo que a carga de teste n o perturba significativamente o sistema; em outras palavras, sup e-se que esta seja muito pequena. A defini o do campo pode ser escrita como:
No caso em que a geometria permita trabalhar de forma unidimensional, la força com massa constante ($F$) por la carga de teste ($q$) pode ser definido introduzindo o campo elétrico ($E$), o que expresso como:
A magnitude de la força com massa constante ($F$) gerada entre duas cargas, representadas por la carga de teste ($q$) e la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada utilizando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte forma:
Usando a defini o do campo el trico como
obt m-se
La força ($\vec{F}$) em la carga de teste ($q$) em la posição ($\vec{r}$) depender de o número de cobranças ($N$), indexado por $i$ e representado por la carga iônica i ($Q_i$) localizado em la posição de uma carga i ($\vec{u}_i$). Com os par metros la constante dielétrica ($\epsilon$) e la constante de campo elétrico ($\epsilon_0$), isso pode ser escrito da seguinte maneira:
Com a defini o de o campo elétrico ($\vec{E}$) dada por
segue que o campo el trico de uma distribui o de cargas
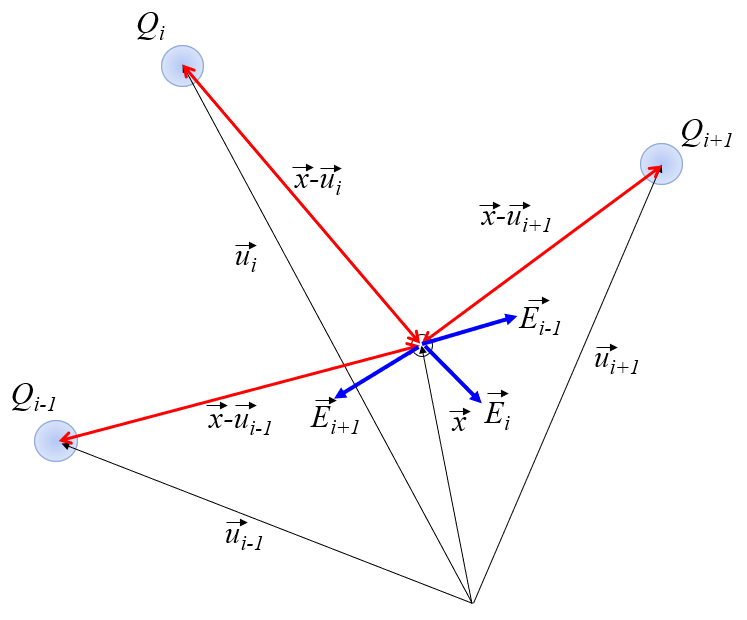
A equa o pode ser representada graficamente da seguinte forma:
La força ($\vec{F}$) para la carga de teste ($q$) definido como o campo elétrico ($\vec{E}$), que expresso como:
La força com massa constante ($F$) para la carga de teste ($q$) definido como o campo elétrico ($E$), que expresso como:
Uma vez que o campo elétrico ($E$) conhecido, la força com massa constante ($F$), que atua sobre la carga ($q$), pode ser calculado usando:
Uma vez conhecido o campo elétrico ($\vec{E}$), la força ($\vec{F}$), que atua em la carga ($q$), pode ser calculado usando:
A magnitude de o campo elétrico ($E$) gerada por la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada utilizando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte forma:
O campo elétrico ($\vec{E}$) em la posição ($\vec{r}$) depender de o número de cobranças ($N$), indexado por $i$ e representado por la carga iônica i ($Q_i$) localizado em la posição de uma carga i ($\vec{u}_i$). Com os par metros la constante dielétrica ($\epsilon$) e la constante de campo elétrico ($\epsilon_0$), isso pode ser escrito da seguinte maneira:
ID:(814, 0)
