Benützer:


Paralleler Widerstand
Storyboard

Wenn die Widerstände parallel geschaltet werden, sind sie alle der gleichen Potentialdifferenz ausgesetzt, die nach dem Ohmschen Gesetz unterschiedliche Ströme erzeugt. Der Gesamtstrom ist die Summe der Teilströme, der Gesamtwiderstand ist also der Kehrwert der Summe der Kehrwerte der Einzelwiderstände.

>Modell

ID:(1397, 0)


Parallele Widerstände (Diagramm)
Definition

Das Diagramm, das parallel geschaltete Widerstände darstellt, hat die folgende Form:
 

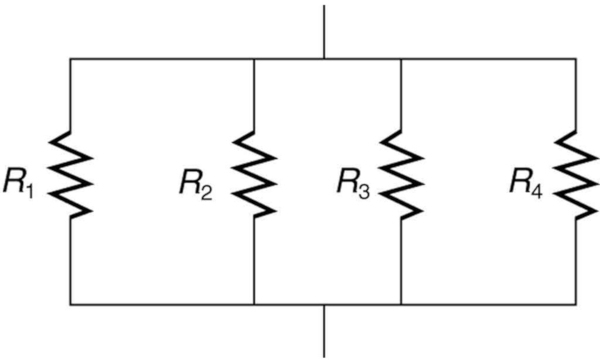
ID:(7861, 0)


Paralleler Widerstand (2)
Beschreibung

Wenn die Widerstände parallel geschaltet werden, sind sie alle der gleichen Potentialdifferenz ausgesetzt, die nach dem Ohmschen Gesetz unterschiedliche Ströme erzeugt. Der Gesamtstrom ist die Summe der Teilströme, der Gesamtwiderstand ist also der Kehrwert der Summe der Kehrwerte der Einzelwiderstände.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$\Delta\varphi$
Dphi
Potentialdifferenz
V
$I$
I
Strom
A
$I_1$
I_1
Strom 1
A
$I_2$
I_2
Strom 2
A
$R_1$
R_1
Widerstand 1
Ohm
$R_2$
R_2
Widerstand 2
Ohm
$R_p$
R_p
Widerstand in Parallel
Ohm

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele


(ID 16032)


(ID 16021)

Der Kehrwert von die Widerstand in Parallel ($R_p$) ist gleich der Summe der Kehrwerte von die Widerstand 1 ($R_1$) und die Widerstand 2 ($R_2$). Diese Beziehung wird wie folgt ausgedr ckt:

$\displaystyle\frac{1}{ R_p }=\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }$

(ID 16006)

Nach dem Prinzip der Erhaltung der elektrischen Ladung ist die Strom ($I$) gleich der Summe von die Strom 1 ($I_1$) und die Strom 2 ($I_2$). Diese Beziehung wird wie folgt ausgedr ckt:

$ I = I_1 + I_2 $

(ID 16009)

Das traditionelle Ohmsche Gesetz stellt eine Beziehung zwischen die Potentialdifferenz ($\Delta\varphi$) und die Strom ($I$) ber die Widerstand ($R$) her, unter Verwendung der folgenden Gleichung:

$ \Delta\varphi = R I $

(ID 3214)

Das traditionelle Ohmsche Gesetz stellt eine Beziehung zwischen die Potentialdifferenz ($\Delta\varphi$) und die Strom ($I$) ber die Widerstand ($R$) her, unter Verwendung der folgenden Gleichung:

$ \Delta\varphi = R I $

(ID 3214)

Das traditionelle Ohmsche Gesetz stellt eine Beziehung zwischen die Potentialdifferenz ($\Delta\varphi$) und die Strom ($I$) ber die Widerstand ($R$) her, unter Verwendung der folgenden Gleichung:

$ \Delta\varphi = R I $

(ID 3214)

ID:(1397, 0)