Usuario:
Resistencia de una inductancia
Definición 
Una inductancia genera según la ley de Lenz un campo que se opone a la corriente que circula por ella lo que se observa como una resistencia. El diagrama para una inductancia conectada a una diferencia de de potencial se muestra a continuación:
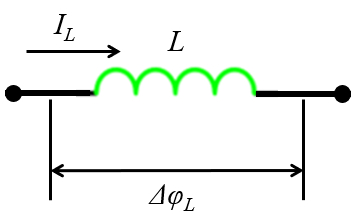
ID:(12270, 0)
Resistencia de una capacitancia
Imagen
Bajo la corriente alterna una capacitancia es periódicamente polarizada y despolarizada existiendo también una resistencia a dicha situación. En este caso se tiene que la capacitancia conectada se describe con el siguiente diagrama:
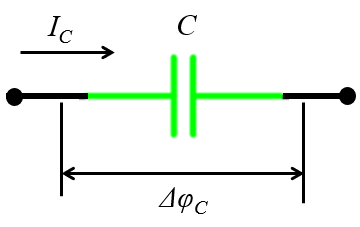
ID:(12271, 0)
Elementos de un circuito de corriente alterna (CA)
Descripción
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 12275)
(ID 14308)
Ejemplos
Una inductancia genera seg n la ley de Lenz un campo que se opone a la corriente que circula por ella lo que se observa como una resistencia. El diagrama para una inductancia conectada a una diferencia de de potencial se muestra a continuaci n:
(ID 12270)
Como el potencial de una impedancia es
| $ \Delta\varphi =- L \displaystyle\frac{ d I }{ d t } $ |
se tiene en el espacio complejo que
| $ \Delta\varphi_L = i\omega L I_L $ |
(ID 14304)
Como el potencial de una capacitancia es
| $ \Delta\varphi =\displaystyle\frac{ Q }{ C }$ |
y la corriente se define como como
| $ I =\displaystyle\frac{ \Delta Q }{ \Delta t }$ |
se tiene que
| $ \displaystyle\frac{d \Delta\varphi_C }{d t }=\displaystyle\frac{ I_C }{ C } $ |
(ID 14305)
Bajo la corriente alterna una capacitancia es peri dicamente polarizada y despolarizada existiendo tambi n una resistencia a dicha situaci n. En este caso se tiene que la capacitancia conectada se describe con el siguiente diagrama:
(ID 12271)
Como el potencial de una capacitancia es
| $ \displaystyle\frac{d \Delta\varphi_C }{d t }=\displaystyle\frac{ I_C }{ C } $ |
en el espacio complejo se tiene que
| $ \Delta\varphi_C = - i \displaystyle\frac{ I_C }{ \omega C } $ |
(ID 14306)
Con la ley de Ohm
| $ \Delta\varphi = R I $ |
se puede generalizar la relaci n en el espacio complejo como
| $ Z = \displaystyle\frac{ \Delta\varphi_R }{ I_R } $ |
(ID 14307)
Si se observan las relaciones de la potencia de la inductancia
| $ \Delta\varphi_L = i\omega L I_L $ |
y de la capacitancia
| $ \Delta\varphi_C = - i \displaystyle\frac{ I_C }{ \omega C } $ |
son an logas a la ley de ohm
| $ Z = \displaystyle\frac{ \Delta\varphi_R }{ I_R } $ |
pero con valores de resistencia complejos. Por ello se puede generalizar el concepto de resistencia a un valor complejo
| $ Z = R + i X $ |
(ID 14308)
La resistencia de una capacitancia depende tanto de la capacitancia de el elemento como la frecuencia angular.
En particular con es
| $ X_C = -\displaystyle\frac{1}{ \omega C } $ |
(ID 12277)
La corriente es proporcional a la diferencia de potencial e inversamente proporcional a la resistencia de la capacitancia lo que corresponde a un tipo de ley de Ohm para una capacitancia.
En particular con es
| $ I_C = \displaystyle\frac{ \Delta\varphi_C }{ X_C }$ |
(ID 12278)
La resistencia de una inductancia depende tanto de la inductividad de el elemento como la frecuencia angular.
En particular con es
| $ X_L = \omega L $ |
(ID 12275)
La corriente es proporcional a la diferencia de potencial e inversamente proporcional a la resistencia de la inductancia lo que corresponde un tipo de ley de Ohm para una inductancia.
En particular con es
| $ I_L = \displaystyle\frac{ \Delta\varphi_L }{ X_L }$ |
(ID 12276)
ID:(1906, 0)