Cálculo de dosis
Storyboard 
Para diseñar el tratamiento es necesario calcular la dosis que recibirá cada elemento del cuerpo. El diseño debe ser tal que la radiación del tejido sano debe ser mínimo mientras que el cancerígeno máximo.
ID:(345, 0)
Calculo de dosis
Definición 
Finalmente calculamos la dosis de cada haz considerando el tiempo de exposición De la suma se obtiene la dosis total y con el modelo L-Q se puede hacer una estimación de la probabilidad de sobre vivencia de las células en la zona de superposición.
El calculo real se realiza con los llamados planificadores que permiten que simulan el efecto de la radiación según perfil, Intensidad y dirección.
ID:(817, 0)
Coeficientes de atenuación másico
Imagen 
En el estudio de la interacción radiación materia tenemos cinco distintos scatterings:
- Coherente o de Rayleigh (R)
- Incoherente o de Compton (C)
- Fotoeléctrico (F)
- Pares (por campo del nucleo) (P)
- Pares (por campo del electrones)
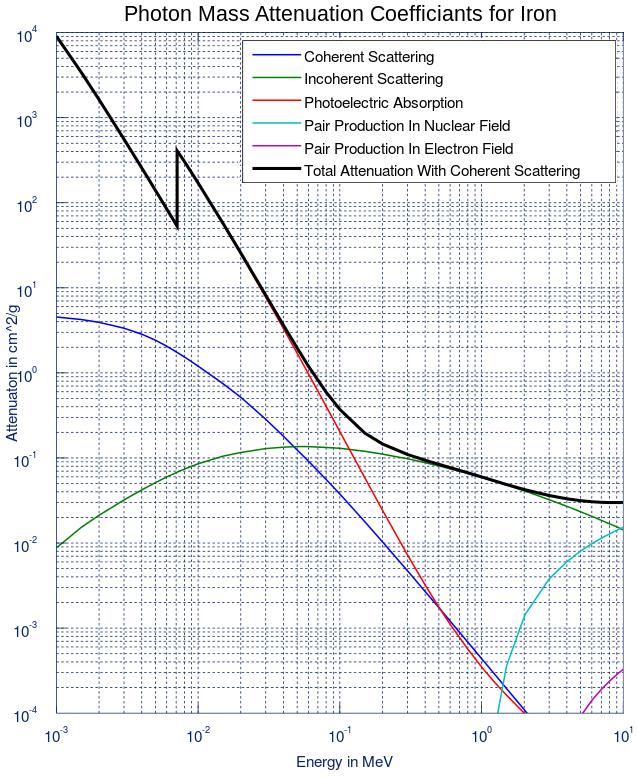
Coeficientes de atenuación másico
Si recordamos que el scattering de Rayleigh no contribuye con los electrones que se necesitan para la terapia vemos que no se debiese trabajar a bajas energías.
Por ello los LINAC trabajan hasta
ID:(3091, 0)
Interacción fotón-materia
Nota 
La interacción entre el foton y la materia se modela mediante el calculo de la probabilidad de que un foton interactue con la materia por distancia recorrida. Dicha probabilidad se denomina sección eficaz. Esta además puede ser expresada como un diferencial
ID:(253, 0)
Monte Carlo
Cita 
El método Pencil Beam + Convolución permite una estimación bastante rápida (segundo a minutos) de la dosis generada lo que lo transforma en una herramienta eficaz en la planificación del plan de tratamiento del paciente. Sin embargo en
ID:(255, 0)
Pencil Beam
Ejercicio 
Uno de los modelos mas simples para el calculo es el denominado Pencil Beam en que uno asume que los fotones de comportan como un rayo (bean) que se desplaza en forma recta (pencil - lápiz - desplazamiento recto como un lápiz). El flujo de fotones, que en la superficie es
ID:(254, 0)
Planificación de tratamiento
Ecuación 
El tratamiento involucra una planificación que no solo incluye la dosis y el numero de sesiones, ademas indica el numero de haces (direcciones) y el perfil de cada uno. Esta es la base lo que se denomina el Intensity-modulated radiation therapy (IMRT) - Radio Terapia de Intensidad Modulada. Con ello se logra un optimo para destruir las células cancerígenas y reguardar al máximo aquellas sanas.
ID:(256, 0)
Valores del coeficiente de atenuación másica
Script 
El coeficiente de atenuación másica corresponde al coeficiente de atenuación
ID:(862, 0)
Cálculo de dosis
Storyboard 
Para diseñar el tratamiento es necesario calcular la dosis que recibirá cada elemento del cuerpo. El diseño debe ser tal que la radiación del tejido sano debe ser mínimo mientras que el cancerígeno máximo.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Finalmente calculamos la dosis de cada haz considerando el tiempo de exposici n De la suma se obtiene la dosis total y con el modelo L-Q se puede hacer una estimaci n de la probabilidad de sobre vivencia de las c lulas en la zona de superposici n.
El calculo real se realiza con los llamados planificadores que permiten que simulan el efecto de la radiaci n seg n perfil, Intensidad y direcci n.
El coeficiente de atenuaci n m sico
Sin embargo como solo los fotones que son originados por efecto fotoelectrico, Compton y Pares la dosis se basara en la suma de solo tres coeficientes de absorci n
Como la secci n eficaz se construye de la suma de las secciones eficaces de cada uno de los m todos de interacci n tenemos un coeficiente de atenuaci n que es la suma del coeficiente de atenuaci n para el scattering de Rayleigh
El coeficiente de atenuaci n m sico
En el estudio de la interacci n radiaci n materia tenemos cinco distintos scatterings:
- Coherente o de Rayleigh (R)
- Incoherente o de Compton (C)
- Fotoel ctrico (F)
- Pares (por campo del nucleo) (P)
- Pares (por campo del electrones)
Coeficientes de atenuaci n m sico
Si recordamos que el scattering de Rayleigh no contribuye con los electrones que se necesitan para la terapia vemos que no se debiese trabajar a bajas energ as.
Por ello los LINAC trabajan hasta
Como se irradia de distintas direcciones existen dosis parciales
Para el calculo de la Dosis se considera la energ a depositada en volumen compuesto por la secci n
donde se incluyo el tiempo
Para el calculo de la dosis se considera la energ a depositada en volumen compuesto por la secci n
donde se incluyo el tiempo
Si se asume que gran parte de los electrones llegan hasta el target y que el sistema opera en del l mite de saturaci n entre filamento y nodo se tiene que el numero de electrones sera del orden de
Si ademas asumimos que cada electr n genera del orden de
o sea
La dosis se calcula de la energ a depositada dividido por la masa que la absorbe. Si consideramos una volumen de largo
En el caso de un cuerpo compuesto de dos materiales con coeficientes de absorci n
La interacci n entre el foton y la materia se modela mediante el calculo de la probabilidad de que un foton interactue con la materia por distancia recorrida. Dicha probabilidad se denomina secci n eficaz. Esta adem s puede ser expresada como un diferencial
La reducci n a
Si el coeficiente de atenuaci n depende del tejido, la ley de Beer-Lambert
se puede generalizar a
El m todo Pencil Beam + Convoluci n permite una estimaci n bastante r pida (segundo a minutos) de la dosis generada lo que lo transforma en una herramienta eficaz en la planificaci n del plan de tratamiento del paciente. Sin embargo en
Uno de los modelos mas simples para el calculo es el denominado Pencil Beam en que uno asume que los fotones de comportan como un rayo (bean) que se desplaza en forma recta (pencil - l piz - desplazamiento recto como un l piz). El flujo de fotones, que en la superficie es
El tratamiento involucra una planificaci n que no solo incluye la dosis y el numero de sesiones, ademas indica el numero de haces (direcciones) y el perfil de cada uno. Esta es la base lo que se denomina el Intensity-modulated radiation therapy (IMRT) - Radio Terapia de Intensidad Modulada. Con ello se logra un optimo para destruir las c lulas cancer genas y reguardar al m ximo aquellas sanas.
Cuando se irradia desde varias direcciones en un mismo tratamiento se pueden sumar las dosis parciales para calcular una dosis total del tratamiento. El calculo debe ser hecho para cada punto del cuerpo irradiado y entrega una distribuci n de dosis.
A modo de ejemplo si las dosis son
El coeficiente de atenuaci n m sica corresponde al coeficiente de atenuaci n
ID:(345, 0)
