Condición de Equilibrio y Temperatura
Storyboard 
Para modelar sistemas con la mecánica estadística, es necesario examinar cómo los parámetros que describen el sistema macroscópico pueden afectar a los ensambles estadísticos. En el caso de partículas, el parámetro de temperatura se establece como un indicador de si los sistemas están en equilibrio, manteniendo sus energías a un nivel constante.
ID:(436, 0)
Un Sistema en contacto con un reservorio
Definición 
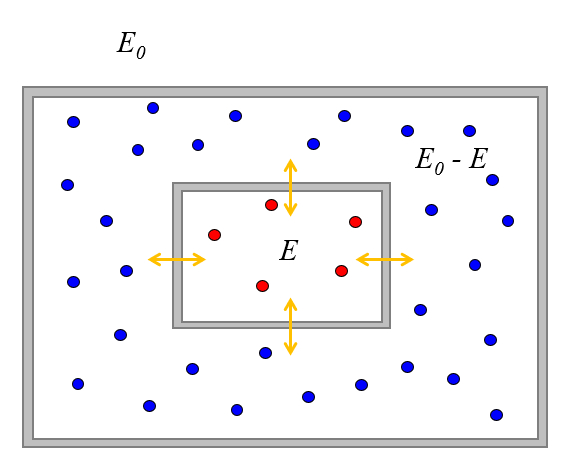
Puedemos estudiar lo que ocurre cuando ponemos dos sistemas de partículas en contacto de manera que puedan intercambiar energía pero no partículas.
Supongamos además que el sistema está aislado del entorno, por lo que tiene una energía total $E_0$.
Supongamos que inicialmente el primer sistema tiene una energía de $E$, lo que se asocia con $\Omega(E)$ estados.
Dado que la energía total es $E_0$, el segundo sistema solo puede tener la energía $E_0-E$ y un número de estados $\Omega(E_0-E)$ asociados.
Una vez que los ponemos en contacto, pueden intercambiar energía hasta alcanzar algún equilibrio. En este sentido, el valor de $E$ va a variar, y la probabilidad de encontrar los sistemas de modo que el primero tenga un valor de $E$ también variará.
ID:(11541, 0)
Comparando las curvas de número de estados
Imagen 
Si comparamos cómo varía el número de estados con la energía $E$, notaremos que el comportamiento del sistema y del reservorio es inverso:
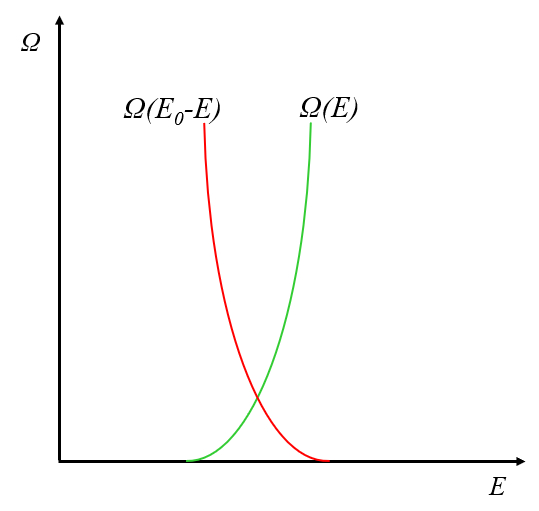
Esto ocurre porque al aumentar la energía del sistema, la del reservorio disminuye, lo que a su vez reduce el número de estados a los que puede acceder.
ID:(11542, 0)
Formación de un máximo
Nota 
Si multiplicamos el número de casos, obtenemos una función con un máximo muy definido.

El sistema tendrá una mayor probabilidad de encontrarse en la energía en la que se encuentra el pico de la curva de probabilidad.
ID:(11543, 0)
Condición de Equilibrio y Temperatura
Descripción 
Para modelar sistemas con la mecánica estadística, es necesario examinar cómo los parámetros que describen el sistema macroscópico pueden afectar a los ensambles estadísticos. En el caso de partículas, el parámetro de temperatura se establece como un indicador de si los sistemas están en equilibrio, manteniendo sus energías a un nivel constante.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3438)
Ejemplos
Puedemos estudiar lo que ocurre cuando ponemos dos sistemas de part culas en contacto de manera que puedan intercambiar energ a pero no part culas.
Supongamos adem s que el sistema est aislado del entorno, por lo que tiene una energ a total $E_0$.
Supongamos que inicialmente el primer sistema tiene una energ a de $E$, lo que se asocia con $\Omega(E)$ estados.
Dado que la energ a total es $E_0$, el segundo sistema solo puede tener la energ a $E_0-E$ y un n mero de estados $\Omega(E_0-E)$ asociados.
Una vez que los ponemos en contacto, pueden intercambiar energ a hasta alcanzar alg n equilibrio. En este sentido, el valor de $E$ va a variar, y la probabilidad de encontrar los sistemas de modo que el primero tenga un valor de $E$ tambi n variar .

(ID 11541)
Cada sistema $\Omega$ tiene un n mero de estados posibles que depende de su energ a $E$. Por lo tanto, si el sistema que estamos estudiando tiene una energ a $E$, el n mero de estados posibles ser $\Omega(E)$.
El sistema en estudio est en contacto con un reservorio que entrega energ a $E$, de modo que la energ a total es $E_0$ menos la del sistema inmerso, $E$. Por lo tanto, el reservorio tiene $\Omega(E_0 - E)$ estados posibles. La probabilidad de encontrar el sistema total con una energ a $E$ en el sistema inmerso es expresada como el producto del n mero de estados con :
| $P(E)=C\Omega(E)\Omega(E_0-E)$ |
donde $C$ es una constante de normalizaci n. La energ a $E$ ser aquella para la cual la probabilidad sea m xima.
(ID 3434)
Si comparamos c mo var a el n mero de estados con la energ a $E$, notaremos que el comportamiento del sistema y del reservorio es inverso:

Esto ocurre porque al aumentar la energ a del sistema, la del reservorio disminuye, lo que a su vez reduce el n mero de estados a los que puede acceder.
(ID 11542)
Si multiplicamos el n mero de casos, obtenemos una funci n con un m ximo muy definido.

El sistema tendr una mayor probabilidad de encontrarse en la energ a en la que se encuentra el pico de la curva de probabilidad.
(ID 11543)
Si la probabilidad de que dos sistemas aislados del resto, con una energ a total $E_0$ y siendo la energ a de uno de los sistemas $E$, est dada por factor de normalización $-$, numero de estados del reservorio con energía $E_0-E$ $-$, numero de estados del sistema con la energía $E$ $-$ y probabilidad del sistema de tener una energía $E$ $-$
| $P(E)=C\Omega(E)\Omega(E_0-E)$ |
Podemos estimar la energ a probable $E$ en la que se encontrar n buscando el m ximo de la probabilidad. Para ello, debemos derivar con respecto a la energ a $E$ e igualar la derivada a cero.
$\displaystyle\frac{\partial P}{\partial E}=\displaystyle\frac{\partial\Omega}{\partial E}\Omega'+\Omega\displaystyle\frac{\partial\Omega'}{\partial E}=0$
Si dividimos la expresi n por $\Omega\Omega'$ y reemplazamos la diferencia de energ as $E_0-E$ por $E'$, podemos reescribir la condici n para determinar la situaci n m s probable como sigue:
Si existe una probabilidad $P(E)$ de encontrar
$\displaystyle\frac{1}{\Omega}\displaystyle\frac{\partial\Omega}{\partial E}-\displaystyle\frac{1}{\Omega'}\displaystyle\frac{\partial\Omega'}{\partial E'}=0$
El signo negativo proviene del cambio de variables, ya que con
$E'=E_0-E$
la derivada en $E'$ resulta con factor de normalización $-$, numero de estados del reservorio con energía $E_0-E$ $-$, numero de estados del sistema con la energía $E$ $-$ y probabilidad del sistema de tener una energía $E$ $-$
| $\displaystyle\frac{1}{\Omega}\displaystyle\frac{\partial\Omega}{\partial E}-\displaystyle\frac{1}{\Omega_h}\displaystyle\frac{\partial\Omega_h}{\partial E_h}=0$ |
(ID 4806)
Cuando un sistema est en contacto con un reservorio de energ a $E_0$, es probable encontrarlo con una energ a $E$ para la cual la probabilidad con factor de normalización $-$, numero de estados del reservorio con energía $E_0-E$ $-$, numero de estados del sistema con la energía $E$ $-$ y probabilidad del sistema de tener una energía $E$ $-$
| $P(E)=C\Omega(E)\Omega(E_0-E)$ |
alcanza su m ximo. La energ a se puede determinar derivando esta expresi n respecto a la energ a $E$ e igual ndola a cero. Esto es equivalente a derivar el logaritmo de la probabilidad:
$\ln P(E) = \ln C + \ln\Omega(E) + \ln\Omega(E_0-E)$
Lo que nos lleva a:
$\displaystyle\frac{\partial\ln\Omega}{\partial E} + \displaystyle\frac{\partial\ln\Omega}{\partial E} = 0$
Si realizamos un cambio de variable:
$E' = E_0 - E$
Obtenemos la condici n de equilibrio con factor de normalización $-$, numero de estados del reservorio con energía $E_0-E$ $-$, numero de estados del sistema con la energía $E$ $-$ y probabilidad del sistema de tener una energía $E$ $-$:
| $\displaystyle\frac{\partial\ln\Omega}{\partial E}-\displaystyle\frac{\partial\ln\Omega_h}{\partial E_h}=0$ |
(ID 3441)
La condici n de equilibrio de un sistema en contacto con un reservorio se expresa con energía del reservorio $J$, energía del sistema $J$, numero de estados del reservorio con energía $E'$ $-$ y numero de estados del sistema con la energía $E$ $-$
| $\displaystyle\frac{\partial\ln\Omega}{\partial E}-\displaystyle\frac{\partial\ln\Omega_h}{\partial E_h}=0$ |
Esto nos permite introducir una funci n $\beta$ con energía del reservorio $J$, energía del sistema $J$, numero de estados del reservorio con energía $E'$ $-$ y numero de estados del sistema con la energía $E$ $-$ de la siguiente manera:
| $\beta(E)\equiv\displaystyle\frac{\partial\ln\Omega}{\partial E}$ |
Esta funci n caracteriza el estado del sistema y es relevante cuando el sistema est en equilibrio con otro sistema.
(ID 3435)
Cuando un sistema est en contacto con un reservorio de energ a $E_0$, es probable encontrarlo con una energ a $E$ para la cual, con , la probabilidad
alcanza su m ximo. La energ a se puede determinar al derivar esta expresi n respecto a la energ a $E$ y establecerla en cero. Esto es equivalente a derivar el logaritmo de la probabilidad:
$\ln P(E) = \ln C + \ln\Omega(E) + \ln\Omega(E_0-E)$
Por lo tanto, con , obtenemos
Si realizamos un cambio de variable
$E' = E_0 - E$
obtenemos la condici n de equilibrio con :
(ID 3436)
Si asumimos que encontramos el sistema en la energ a para la cual la probabilidad es m xima, podemos asociar este hecho con la situaci n de equilibrio de un sistema, donde la probabilidad es m xima.
Por otro lado, sabemos que dos sistemas est n en equilibrio t rmico si sus temperaturas son iguales. Por lo tanto, el hecho de que las funciones $\beta$ sean iguales nos sugiere que $\beta$ est relacionada con la temperatura.
Dado que las unidades de $\beta$ son el rec proco de la energ a, podemos definirlo de la siguiente manera con :
| $ k_B T \equiv\displaystyle\frac{1}{ \beta }$ |
(ID 3437)
Al introducir la relaci n con beta del reservorio $1/J$, constante de Boltzmann $J/K$ y temperatura del sistema $K$
| $ k_B T \equiv\displaystyle\frac{1}{ \beta }$ |
la condici n de equilibrio con beta del reservorio $1/J$ y beta del sistema $1/J$
| $\beta(E)=\beta(E_h)$ |
se reduce con beta del reservorio $1/J$ y beta del sistema $1/J$ a simplemente
| $ T = T_h $ |
(ID 3438)
ID:(436, 0)
