Travail
Storyboard 
Le travail dépend de la manière dont le processus se déroule. Par exemple, il représente l'énergie nécessaire pour appliquer une force spécifique afin de déplacer un corps sur une certaine distance, ou la pression qui doit être maintenue sur un gaz pour lui permettre de s'étendre sur un volume spécifique.
ID:(1470, 0)
Mécanismes
Définition 
En thermodynamique, le travail est l'énergie transférée vers ou depuis un système par une force agissant sur une distance. Cela peut se produire sous différentes formes, comme le travail mécanique, où un gaz dans un cylindre avec un piston se dilate et déplace le piston, ou le travail électrique, impliquant le transfert d'énergie par des forces électriques. Le concept de travail est crucial pour comprendre les échanges d'énergie et les processus. Il est souvent représenté mathématiquement, impliquant des changements de pression et de volume dans le système. Selon la première loi de la thermodynamique, la variation de l'énergie interne d'un système est égale à la chaleur ajoutée au système moins le travail effectué par le système sur son environnement. Le travail est essentiel dans divers processus, y compris les processus isothermes, adiabatiques, isobares et isochoriques, et il est fondamental dans des applications telles que les moteurs thermiques et les réfrigérateurs, où il joue un rôle clé dans la conversion de la chaleur en travail ou l'utilisation du travail pour transférer de la chaleur.
ID:(15247, 0)
Convertisseur travail-chaleur
Image 
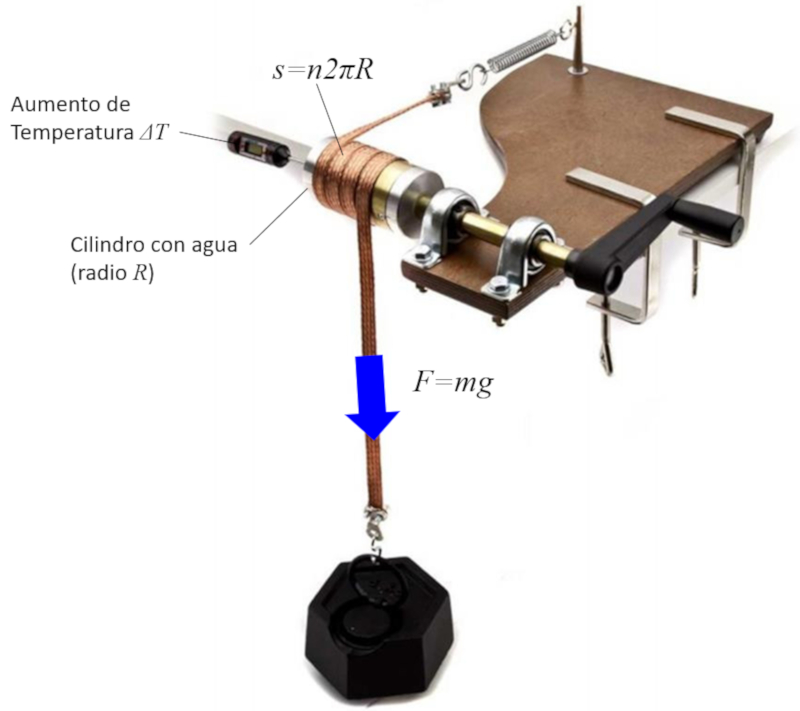
La conversion du travail en énergie est étudiée en générant de la chaleur par frottement. Pour cela, on entoure un cylindre contenant de l'eau et un thermomètre d\'une bande métallique. En tournant la manivelle, la chaleur est générée par frottement, ce qui entraîne le réchauffement de l\'eau. Si l\'on mesure la force appliquée, le nombre de tours effectués et le rayon du cylindre, on peut estimer la distance parcourue, ce qui permet d\'estimer l\'énergie comme le produit de la force par la distance.
ID:(1884, 0)
Pression et travail
Noter 
Considérons un gaz dans un cylindre où un piston peut se déplacer. Si le piston est déplacé, il est possible de réduire le volume en comprimant le gaz. Pour réaliser cette compression, de l'énergie est nécessaire, équivalente à la force exercée par le gaz multipliée par la distance parcourue par le piston. Cette énergie peut également être représentée en fonction de la pression, puisque la pression est définie par la force et la surface du piston.
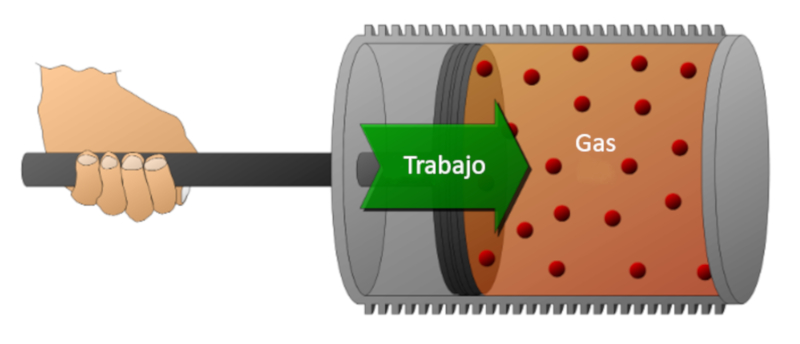
Le travail peut être effectué sur le système (compression) ou par le système sur l'environnement externe (expansion).
Étant donné que a force mécanique ($F$) divisé par a section ($S$) est égal à A pression ($p$) :
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
et que a variation de volume ($\Delta V$) avec le distance parcourue ($dx$) est égal à :
| $ \Delta V = S \Delta s $ |
L'équation pour le différentiel de travail inexact ($\delta W$) peut être exprimée comme suit :
| $ \Delta W = F \Delta s $ |
Elle peut donc être écrite comme :
| $ \delta W = p dV $ |
ID:(11126, 0)
Pression et travail sur un gaz
Citation 
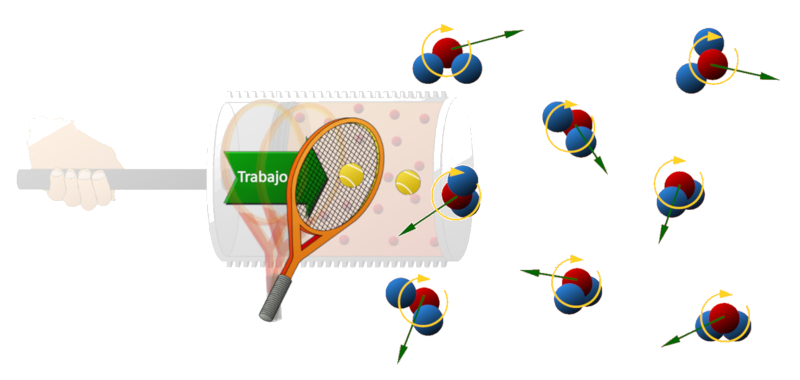
Lorsque le piston se déplace dans le cylindre, il agit comme une raquette de tennis, conférant de l'énergie cinétique aux molécules et augmentant leur vitesse. À mesure que ces molécules gagnent en vitesse, elles transfèrent un élan plus important aux parois, ce qui génère une augmentation de la pression.
ID:(11127, 0)
Pression et travail dans un liquide/solide
Exercer 
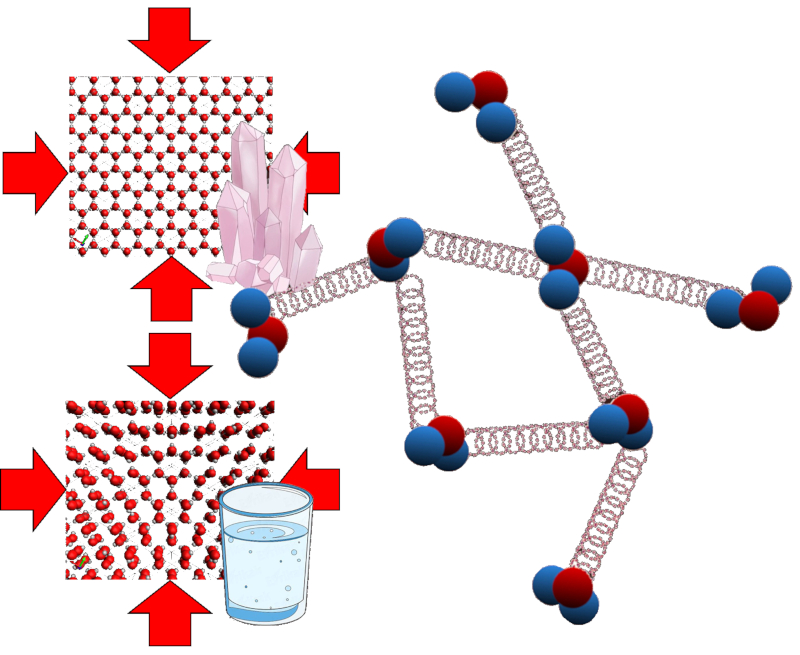
Dans le cas d'un liquide ou d\'un solide, une force externe déplace les particules du matériau, ce qui affecte l\'énergie potentielle des liaisons entre elles. On peut imaginer cela comme de petits ressorts qui se compriment, ce qui augmente leur énergie potentielle.
ID:(11128, 0)
Travail
Description 
Le travail dépend de la manière dont le processus se déroule. Par exemple, il représente l'énergie nécessaire pour appliquer une force spécifique afin de déplacer un corps sur une certaine distance, ou la pression qui doit être maintenue sur un gaz pour lui permettre de s'étendre sur un volume spécifique.
Variables
Calculs
Calculs
Équations
(ID 3202)
tant donn que a force mécanique ($F$) divis par a section ($S$) est gal a pression ($p$) :
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
et que a variation de volume ($\Delta V$) avec le distance parcourue ($dx$) est gal :
| $ \Delta V = S \Delta s $ |
L' quation pour le différentiel de travail inexact ($\delta W$) peut tre exprim e comme suit :
| $ \Delta W = F \Delta s $ |
Elle peut donc tre crite comme :
| $ \delta W = p dV $ |
(ID 3468)
Exemples
En thermodynamique, le travail est l' nergie transf r e vers ou depuis un syst me par une force agissant sur une distance. Cela peut se produire sous diff rentes formes, comme le travail m canique, o un gaz dans un cylindre avec un piston se dilate et d place le piston, ou le travail lectrique, impliquant le transfert d' nergie par des forces lectriques. Le concept de travail est crucial pour comprendre les changes d' nergie et les processus. Il est souvent repr sent math matiquement, impliquant des changements de pression et de volume dans le syst me. Selon la premi re loi de la thermodynamique, la variation de l' nergie interne d'un syst me est gale la chaleur ajout e au syst me moins le travail effectu par le syst me sur son environnement. Le travail est essentiel dans divers processus, y compris les processus isothermes, adiabatiques, isobares et isochoriques, et il est fondamental dans des applications telles que les moteurs thermiques et les r frig rateurs, o il joue un r le cl dans la conversion de la chaleur en travail ou l'utilisation du travail pour transf rer de la chaleur.
(ID 15247)
La conversion du travail en nergie est tudi e en g n rant de la chaleur par frottement. Pour cela, on entoure un cylindre contenant de l'eau et un thermom tre d\'une bande m tallique. En tournant la manivelle, la chaleur est g n r e par frottement, ce qui entra ne le r chauffement de l\'eau. Si l\'on mesure la force appliqu e, le nombre de tours effectu s et le rayon du cylindre, on peut estimer la distance parcourue, ce qui permet d\'estimer l\' nergie comme le produit de la force par la distance.

(ID 1884)
Consid rons un gaz dans un cylindre o un piston peut se d placer. Si le piston est d plac , il est possible de r duire le volume en comprimant le gaz. Pour r aliser cette compression, de l' nergie est n cessaire, quivalente la force exerc e par le gaz multipli e par la distance parcourue par le piston. Cette nergie peut galement tre repr sent e en fonction de la pression, puisque la pression est d finie par la force et la surface du piston.

Le travail peut tre effectu sur le syst me (compression) ou par le syst me sur l'environnement externe (expansion).
tant donn que a force mécanique ($F$) divis par a section ($S$) est gal a pression ($p$) :
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
et que a variation de volume ($\Delta V$) avec le distance parcourue ($dx$) est gal :
| $ \Delta V = S \Delta s $ |
L' quation pour le différentiel de travail inexact ($\delta W$) peut tre exprim e comme suit :
| $ \Delta W = F \Delta s $ |
Elle peut donc tre crite comme :
| $ \delta W = p dV $ |
(ID 11126)
Lorsque le piston se d place dans le cylindre, il agit comme une raquette de tennis, conf rant de l' nergie cin tique aux mol cules et augmentant leur vitesse. mesure que ces mol cules gagnent en vitesse, elles transf rent un lan plus important aux parois, ce qui g n re une augmentation de la pression.

(ID 11127)
Dans le cas d'un liquide ou d\'un solide, une force externe d place les particules du mat riau, ce qui affecte l\' nergie potentielle des liaisons entre elles. On peut imaginer cela comme de petits ressorts qui se compriment, ce qui augmente leur nergie potentielle.

(ID 11128)
(ID 15306)
A écart de travail ($\Delta W$) est défini comme le produit de a force à masse constante ($F$) et a distance parcourue en un temps ($\Delta s$) :
| $ \Delta W = F \Delta s $ |
(ID 3202)
Le différentiel de travail inexact ($\delta W$) est gal a pression ($p$) multipli par a variation de volume ($\Delta V$)xa0:
| $ \delta W = p dV $ |
(ID 3468)
Le travail efficace ($W$) est gal l'int grale de a pression ($p$) par rapport le volume ($V$) de $V_1$ $V_2$. Cela repr sente le travail effectu par la machine, qui peut tre exprim comme suit :
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
(ID 10253)
ID:(1470, 0)
