Soulever
Storyboard 
Le flux autour d'une aile entraîne la formation de tourbillons qui, en fonction de la forme et de l'angle de l'aile par rapport à l'écoulement, peuvent générer des tourbillons sur une section de celle-ci. Si l'on considère des éléments de volume autour de l'aile et que l'on suppose que la conservation de l'énergie peut être localement appliquée, différentes vitesses entraîneront différentes pressions (loi de Bernoulli) sur la surface.
La somme de toutes les pressions sur la surface dans la direction verticale, à la fois sur l'aile (force vers le bas) et sous l'aile (force vers le haut), conduit à une force totale que l'on appelle portance. Si cette force est positive, nous pouvons surmonter la gravité et faire que l'objet (avion/oiseau) s'élève.
ID:(463, 0)
Aile génératrice de portance
Image 
En observant l'écoulement moyen autour d'une aile, on peut remarquer que les lignes au-dessus de l'aile sont plus longues que celles en dessous. En termes simplifiés, on argumente qu'en raison de ce trajet plus long, on s'attend à ce que a vitesse au sommet ($v_t$) soit supérieur à A vitesse en bas ($v_b$), bien que les deux soient supérieurs à A vitesse par rapport au milieu ($v$).
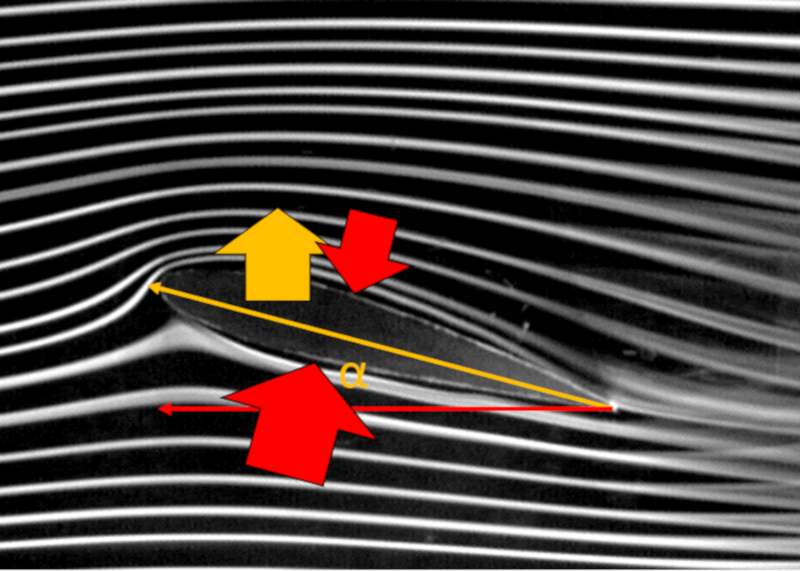
Si la loi de Bernoulli est applicable, la différence de vitesses entraînerait une différence de pressions agissant sur l'aile. En particulier, si a vitesse au sommet ($v_t$) est supérieur, son correspondant a pression sur le dessus de l'aile ($p_t$) serait inférieur à celui avec a vitesse en bas ($v_b$) et son correspondant a pression sur le bas de l'aile ($p_b$). Cela impliquerait l'existence d'un a force de levage ($F_L$) en raison de l'effet de cette différence de pression.
Cependant, comme on le voit vers la fin du profil de l'aile (côté droit), des turbulences se forment, limitant l'applicabilité du principe de Bernoulli. En particulier, il convient de considérer qu'en certaines parties de la circonférence de l'aile, son application peut être limitée et ne contribuera pas à la portance.
ID:(11075, 0)
Circulation autour d'un objet
Noter 
Pour définir la circulation, nous devons d'abord établir le chemin qui sera suivi autour de l'objet/de l'aile dans le sens inverse des aiguilles d'une montre, comme indiqué dans l'image suivante :
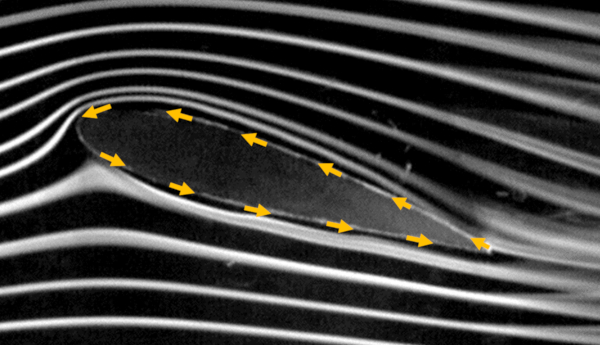
La circulation est définie comme le produit du périmètre autour de l'objet par la projection de la vitesse sur la surface. Comme cette projection de vitesse peut varier le long du périmètre, nous devons la sommer à travers des éléments infinitésimaux du périmètre, où la projection de la vitesse est calculée en utilisant le produit scalaire entre elle et l'élément de périmètre. Graphiquement, cela est représenté comme suit :
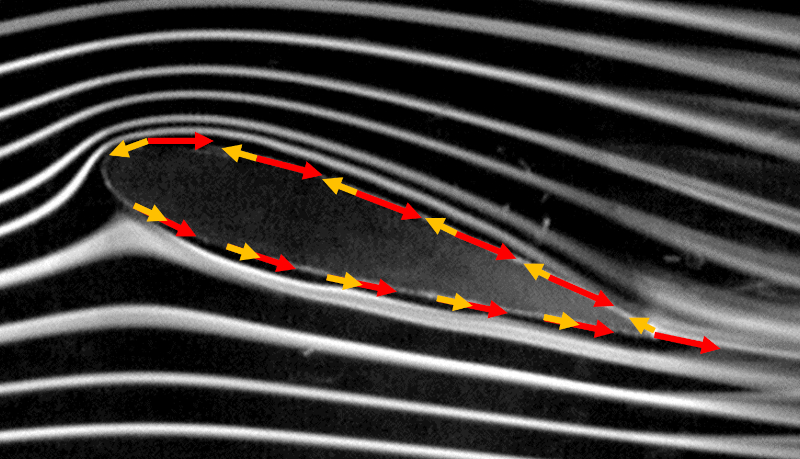
Mathématiquement, cela s'exprime par l'intégrale de ligne fermée du produit scalaire mentionné précédemment :
| $ \Gamma =\displaystyle\oint_C \vec{v} \cdot d\vec{l} $ |
Étant donné que la somme est effectuée dans le sens contraire des aiguilles d'une montre, dans la partie supérieure, la direction dans laquelle pointent les éléments du périmètre est opposée à la direction de la vitesse. Dans la partie inférieure, les deux pointent dans la même direction, ce qui conduit à ce que la partie supérieure annule partiellement la partie inférieure.
ID:(1167, 0)
Théorème de Kutta-Joukowski
Citation 
La relation entre a circulation aérodynamique ($\Gamma$) et l'écoulement autour de l'objet est établie grâce au théorème de Kutta-Joukowski, ce qui permet le calcul de a force de levage ($F_L$) en utilisant a envergure des ailes ($L$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) de la manière suivante :
En simplifiant la modélisation de l'écoulement autour de l'objet, il devient possible d'estimer la circulation en utilisant a surface génératrice de portance ($S_w$) et le coefficient de portance ($C_L$) avec l'équation suivante :
Par conséquent, a force de levage ($F_L$) peut être approximé avec l'équation suivante :
Dans ce contexte, le coefficient de portance ($C_L$) encapsule les effets aérodynamiques de l'objet.
[1] "Über die Aufgabe der Flügeltheorie und ein neues Verfahren zur Herleitung derselben." (Sur la tâche de la théorie des ailes et une nouvelle méthode pour sa dérivation), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1902)
[2] "Über die Erhaltung des Luftkreises um ein Profil." (Sur la conservation du cercle d'air autour d'un profil), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1904)
ID:(1168, 0)
Coefficient de portance
Exercer 
Le coefficient de portance est une fonction de l'angle d\'attaque et suit généralement la tendance indiquée dans la figure suivante :

Dans le cas illustré, la pente est d\'environ 1,5 pour 15 degrés, ce qui correspond à 0,1 1/degré ou 5,73 1/radian.
ID:(7148, 0)
Force de levage dans le flux
Équation 
La différence de pression entre la face inférieure et supérieure de l'aile génère la force de portance, représentée par une flèche perpendiculaire à la surface de l'aile. Cette force s'oppose à la force gravitationnelle qui agit vers le bas :

Les oiseaux ou les avions peuvent voler lorsque la force de portance dépasse la force gravitationnelle.
ID:(7036, 0)
Le décollage d'un avion
Script 
La différence de pression entre la face inférieure et supérieure de l'aile génère la force de portance, représentée par une flèche perpendiculaire à la surface de l'aile. Cette force s\'oppose à la force gravitationnelle qui agit vers le bas :
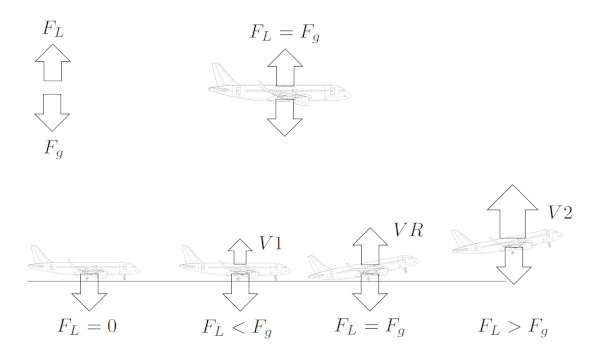
Les oiseaux ou les avions peuvent voler lorsque la force de portance dépasse la force gravitationnelle.
ID:(15157, 0)
Soulever
Description 
Le flux autour d'une aile entraîne la formation de tourbillons qui, en fonction de la forme et de l'angle de l'aile par rapport à l'écoulement, peuvent générer des tourbillons sur une section de celle-ci. Si l'on considère des éléments de volume autour de l'aile et que l'on suppose que la conservation de l'énergie peut être localement appliquée, différentes vitesses entraîneront différentes pressions (loi de Bernoulli) sur la surface. La somme de toutes les pressions sur la surface dans la direction verticale, à la fois sur l'aile (force vers le bas) et sous l'aile (force vers le haut), conduit à une force totale que l'on appelle portance. Si cette force est positive, nous pouvons surmonter la gravité et faire que l'objet (avion/oiseau) s'élève.
Variables
Calculs
Calculs
Équations
(ID 4416)
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous consid rons a surface génératrice de portance ($S_w$), d fini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
et pour le coefficient de portance ($C_L$), d fini comme
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
nous obtenons
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
(ID 4441)
A force de levage ($F_L$) avec a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$) et a vitesse par rapport au milieu ($v$) est repr sent par
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ce qui, avec a masse corporelle ($m$) et a accélération gravitationnelle ($g$), doit tre gal :
| $ F_g = m g $ |
c'est- -dire :
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
ce qui donne :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4442)
Le coefficient de portance ($C_L$) est calcul avec a masse corporelle ($m$), a accélération gravitationnelle ($g$), a surface génératrice de portance ($S_w$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) comme suit :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Ainsi, avec a constante de proportionnalité du coefficient de portance ($c$) et le accélération maximale ($\alpha$),
| $ C_L = c \alpha $ |
nous obtenons
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4443)
(ID 14515)
(ID 15152)
(ID 15153)
A force de levage ($F_L$) d pend de a surface génératrice de portance ($S_w$) et de a différence de pression sur un objet ($\Delta p$) comme suit
| $ F_L = S_w \Delta p $ |
dans l'expression de a force de levage ($F_L$) avec a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$)
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
contient le facteur a envergure des ailes ($L$) qui est associ a surface génératrice de portance ($S_w$). Cependant, les deux peuvent tre associ s si l'on consid re la largeur de l'aile comme la moyenne de a longueur de l'aile supérieure ($l_t$) et de a longueur de l'aile inférieure ($l_b$). Cela nous conduit obtenir
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
(ID 15154)
A force de levage ($F_L$) en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$), et a vitesse par rapport au milieu ($v$) se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous consid rons a surface génératrice de portance ($S_w$) d termin par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$), et a longueur de l'aile inférieure ($l_b$)
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
nous pouvons r crire l' quation pour a force de levage ($F_L$) comme
$F_L =\displaystyle\frac{1}{2} \rho S_w \displaystyle\frac{4(c_bl_b-c_tl_t)}{l_b+l_t} v^2$
ce qui nous permet d'introduire le coefficient de portance :
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
(ID 15155)
A force de levage ($F_L$) est li a circulation aérodynamique ($\Gamma$), a envergure des ailes ($L$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) comme suit :
| $ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$ |
Puisque a circulation aérodynamique ($\Gamma$) est li le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$) comme suit :
| $$ |
Nous pouvons conclure que :
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
(ID 15156)
A circulation aérodynamique ($\Gamma$) est d fini en fonction des longueurs a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$) ainsi que des vitesses a vitesse au sommet ($v_t$) et a vitesse en bas ($v_b$), comme suit :
$\Gamma = -l_t v_t + l_b v_b$
Si a vitesse au sommet ($v_t$) est proportionnel le facteur de vitesse maximale de l'aile ($c_t$) par rapport a vitesse par rapport au milieu ($v$) :
| $ v_t = c_t v $ |
et a vitesse en bas ($v_b$) est proportionnel le facteur de vitesse en bas d'aile ($c_b$) par rapport a vitesse par rapport au milieu ($v$) :
| $ v_b = c_b v $ |
nous pouvons l'exprimer comme suit :
$\Gamma = -l_t c_t v + l_b c_b v$
Cela nous conduit l' quation suivante :
| $ \Gamma = ( c_b l_b - c_t l_t ) v $ |
(ID 15193)
Lorsque l'on relie a circulation aérodynamique ($\Gamma$) Le facteur de vitesse en bas d'aile ($c_b$), le facteur de vitesse maximale de l'aile ($c_t$), a longueur de l'aile inférieure ($l_b$) et a longueur de l'aile supérieure ($l_t$), nous obtenons :
En estimant a surface génératrice de portance ($S_w$) avec a envergure des ailes ($L$) l'aide de :
et en calculant le coefficient de portance ($C_L$) avec :
Le r sultat est :
(ID 15195)
Exemples
(ID 15181)
En observant l' coulement moyen autour d'une aile, on peut remarquer que les lignes au-dessus de l'aile sont plus longues que celles en dessous. En termes simplifi s, on argumente qu'en raison de ce trajet plus long, on s'attend ce que a vitesse au sommet ($v_t$) soit sup rieur a vitesse en bas ($v_b$), bien que les deux soient sup rieurs a vitesse par rapport au milieu ($v$).

Si la loi de Bernoulli est applicable, la diff rence de vitesses entra nerait une diff rence de pressions agissant sur l'aile. En particulier, si a vitesse au sommet ($v_t$) est sup rieur, son correspondant a pression sur le dessus de l'aile ($p_t$) serait inf rieur celui avec a vitesse en bas ($v_b$) et son correspondant a pression sur le bas de l'aile ($p_b$). Cela impliquerait l'existence d'un a force de levage ($F_L$) en raison de l'effet de cette diff rence de pression.
Cependant, comme on le voit vers la fin du profil de l'aile (c t droit), des turbulences se forment, limitant l'applicabilit du principe de Bernoulli. En particulier, il convient de consid rer qu'en certaines parties de la circonf rence de l'aile, son application peut tre limit e et ne contribuera pas la portance.
(ID 11075)
Pour d finir la circulation, nous devons d'abord tablir le chemin qui sera suivi autour de l'objet/de l'aile dans le sens inverse des aiguilles d'une montre, comme indiqu dans l'image suivante :

La circulation est d finie comme le produit du p rim tre autour de l'objet par la projection de la vitesse sur la surface. Comme cette projection de vitesse peut varier le long du p rim tre, nous devons la sommer travers des l ments infinit simaux du p rim tre, o la projection de la vitesse est calcul e en utilisant le produit scalaire entre elle et l' l ment de p rim tre. Graphiquement, cela est repr sent comme suit :

Math matiquement, cela s'exprime par l'int grale de ligne ferm e du produit scalaire mentionn pr c demment :
| $ \Gamma =\displaystyle\oint_C \vec{v} \cdot d\vec{l} $ |
tant donn que la somme est effectu e dans le sens contraire des aiguilles d'une montre, dans la partie sup rieure, la direction dans laquelle pointent les l ments du p rim tre est oppos e la direction de la vitesse. Dans la partie inf rieure, les deux pointent dans la m me direction, ce qui conduit ce que la partie sup rieure annule partiellement la partie inf rieure.
(ID 1167)
La relation entre a circulation aérodynamique ($\Gamma$) et l' coulement autour de l'objet est tablie gr ce au th or me de Kutta-Joukowski, ce qui permet le calcul de a force de levage ($F_L$) en utilisant a envergure des ailes ($L$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) de la mani re suivante :
En simplifiant la mod lisation de l' coulement autour de l'objet, il devient possible d'estimer la circulation en utilisant a surface génératrice de portance ($S_w$) et le coefficient de portance ($C_L$) avec l' quation suivante :
Par cons quent, a force de levage ($F_L$) peut tre approxim avec l' quation suivante :
Dans ce contexte, le coefficient de portance ($C_L$) encapsule les effets a rodynamiques de l'objet.
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sur la t che de la th orie des ailes et une nouvelle m thode pour sa d rivation), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sur la conservation du cercle d'air autour d'un profil), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
(ID 1168)
Le coefficient de portance est une fonction de l'angle d\'attaque et suit g n ralement la tendance indiqu e dans la figure suivante :

Dans le cas illustr , la pente est d\'environ 1,5 pour 15 degr s, ce qui correspond 0,1 1/degr ou 5,73 1/radian.
(ID 7148)
La diff rence de pression entre la face inf rieure et sup rieure de l'aile g n re la force de portance, repr sent e par une fl che perpendiculaire la surface de l'aile. Cette force s'oppose la force gravitationnelle qui agit vers le bas :

Les oiseaux ou les avions peuvent voler lorsque la force de portance d passe la force gravitationnelle.
(ID 7036)
La diff rence de pression entre la face inf rieure et sup rieure de l'aile g n re la force de portance, repr sent e par une fl che perpendiculaire la surface de l'aile. Cette force s\'oppose la force gravitationnelle qui agit vers le bas :

Les oiseaux ou les avions peuvent voler lorsque la force de portance d passe la force gravitationnelle.
(ID 15157)
(ID 15184)
Lorsqu'un objet est immerg dans un flux avec une densit d' nergie constante, il divise le flux en un sup rieur avec a vitesse au sommet ($v_t$) et un inf rieur avec a vitesse en bas ($v_b$). La vitesse est li e la pression g n r e, donc il y a aussi a pression sur le dessus de l'aile ($p_t$) dans la partie sup rieure et a pression sur le bas de l'aile ($p_b$) dans la partie inf rieure. De cette mani re, a différence de pression sur un objet ($\Delta p$)
| $ \Delta p = p_b - p_t $ |
est g n r , ce qui produit son tour une force de levage ($F_L$) pour contrebalancer la force gravitationnelle g n r e par a masse corporelle ($m$) avec a accélération gravitationnelle ($g$).
(ID 1173)
Si une diff rence de pression $\Delta p$ est cr e entre la partie inf rieure et sup rieure d'une aile d\'une surface $S_w$, la force r sultante est appel e force de portance et est calcul e comme suit :
| $ F_L = S_w \Delta p $ |
Cette force de portance est g n r e en raison de la diff rence de pression et est responsable de soutenir le vol d\'un a ronef.
(ID 4416)
Avec l' coulement autour de l'objet connu sous sa forme vectorielle sur toute la surface, il est possible de calculer a circulation aérodynamique ($\Gamma$) par int gration le long d'un chemin ferm , comme illustr ci-dessous :
| $ \Gamma =\displaystyle\oint_C \vec{v} \cdot d\vec{l} $ |
(ID 15194)
Dans le cas de l' coulement passant au-dessus de l'objet/de l'aile, il est n cessaire d'identifier le point de d part et le point d'arr t pour d finir la longueur du trajet a longueur de l'aile supérieure ($l_t$) :
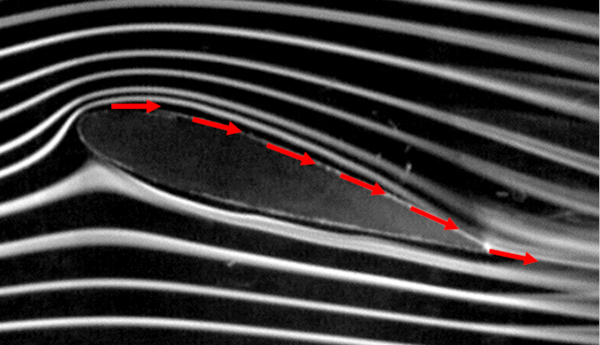
Si nous supposons que a vitesse au sommet ($v_t$) est constant, nous pouvons d duire l'existence de un facteur de vitesse maximale de l'aile ($c_t$) de telle mani re que, avec a vitesse par rapport au milieu ($v$), nous ayons :
| $ v_t = c_t v $ |
(ID 15152)
Dans le cas de l' coulement passant sous l'objet/l'aile, il est n cessaire d'identifier le point de d part et le point d'arr t pour d finir la longueur du trajet a longueur de l'aile inférieure ($l_b$) :
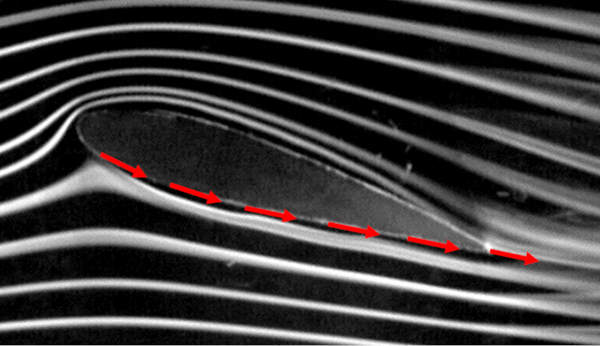
Si nous supposons que a vitesse en bas ($v_b$) est constant, nous pouvons d duire l'existence de un facteur de vitesse en bas d'aile ($c_b$) de telle mani re que, avec a vitesse par rapport au milieu ($v$), nous ayons :
| $ v_b = c_b v $ |
(ID 15153)
Pour obtenir une estimation simplifi e de la circulation, nous pouvons supposer que la vitesse est constante sur la partie sup rieure du p rim tre a vitesse au sommet ($v_t$) et galement sur la partie inf rieure a vitesse en bas ($v_b$). Si ces vitesses sont proportionnelles a vitesse par rapport au milieu ($v$) avec le facteur de vitesse maximale de l'aile ($c_t$) et le facteur de vitesse en bas d'aile ($c_b$), et que les longueurs sont a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$), alors a circulation aérodynamique ($\Gamma$) est calcul comme suit :
| $ \Gamma = ( c_b l_b - c_t l_t ) v $ |
(ID 15193)
D'apr s les travaux de Kutta [1] et Joukowski [2], un th or me a t d velopp montrant l'association entre a circulation aérodynamique ($\Gamma$) et a force de levage ($F_L$) travers a envergure des ailes ($L$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) comme suit :
| $ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$ |
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sur la t che de la th orie des ailes et une nouvelle m thode pour sa d rivation), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sur la conservation du cercle d'air autour d'un profil), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
(ID 1166)
A force de levage ($F_L$) est li a circulation aérodynamique ($\Gamma$), a envergure des ailes ($L$) A densité ($\rho$) et a vitesse par rapport au milieu ($v$) comme suit :
| $ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$ |
Par cons quent, avec l'estimation de a circulation aérodynamique ($\Gamma$) en fonction de le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$), nous obtenons :
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
(ID 15156)
A surface génératrice de portance ($S_w$) est gal a envergure des ailes ($L$) divis par le largeur de l'aile ($w$), et ce dernier peut tre estim comme la moyenne de a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$), ce qui donne :
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
(ID 15154)
Le coefficient de portance ($C_L$) peut tre calcul en fonction de a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$), le facteur de vitesse maximale de l'aile ($c_t$) et le facteur de vitesse en bas d'aile ($c_b$) comme suit :
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
(ID 15155)
A circulation aérodynamique ($\Gamma$) se r sume finalement en un calcul impliquant a surface génératrice de portance ($S_w$), a envergure des ailes ($L$), le coefficient de portance ($C_L$) et a vitesse par rapport au milieu ($v$) travers l' quation :
| $ \Gamma = \displaystyle\frac{ S_w }{2 L } C_L v ^2$ |
(ID 15195)
Pour g n rer une pression plus lev e en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilis pour corriger le manque de conservation de la densit d' nergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut tre estim e en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) gr ce la formule suivante :
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
Pour qu'un vaisseau spatial ou un oiseau puisse rester en vol, a force gravitationnelle ($F_g$) doit contrer la force de la gravit , d finie par a masse corporelle ($m$) et a accélération gravitationnelle ($g$). En d'autres termes, il doit tre :
| $ F_g = m g $ |
Il s'agit d'une situation simplifi e qui ne tient pas compte du fait que la force de r sistance peut galement g n rer une force de portance.
(ID 14515)
partir de mesures, il est conclu que le coefficient de portance $C_L$ est proportionnel l'angle d\'attaque $\alpha$:
| $ C_L = c \alpha $ |
Apr s un certain angle, la courbe diminue jusqu\' atteindre z ro. Cela est d au fait que au-del de cet angle critique, les tourbillons recouvrent enti rement la surface sup rieure de l\'aile, ce qui entra ne une perte de portance. Ce ph nom ne est appel \"d crochage\" ou \"d crochage a rodynamique\".
(ID 4441)
La condition pour atteindre le vol est remplie lorsque a force de levage ($F_L$) est gal au poids de l'a ronef ou de l'oiseau, calcul partir de a masse corporelle ($m$) et a accélération gravitationnelle ($g$). Cela est r alis avec des valeurs suffisantes de ERROR:6110,0, a surface génératrice de portance ($S_w$), et le coefficient de portance ($C_L$), ce dernier coefficient tant le facteur ajustable. Dans le cas des a ronefs, les pilotes peuvent modifier la valeur de le coefficient de portance ($C_L$) en utilisant les volets, dont la valeur doit satisfaire :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Les volets sont ajust s en modifiant l'angle que l'aile forme avec la direction du vol, connu sous le nom d'angle d'attaque.
(ID 4442)
tant donn que le coefficient de portance $C_L$ est proportionnel l'angle d'attaque $\alpha$, on peut calculer l'angle n cessaire pour obtenir une portance suffisante pour une vitesse $v$ donn e :
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
o $m$ est la masse, $g$ est l\'acc l ration due la gravit , $\rho$ est la densit du milieu, $S_w$ est la surface de l\'aile et $c$ est la constante de proportionnalit entre le coefficient de portance et l\'angle d\'attaque.
(ID 4443)
ID:(463, 0)
