Movement on coastal edges
Storyboard 
At the shoreline, Coriolis force can lead to circulation that draws nutrient-rich material to the surface (Ekman transport).
ID:(1578, 0)
Ekman Transport
Image 
Cuando existen corrientes en dirección del ecuador en los lados oeste en bordes continentales, la ecuación de Coriolis para el plano con
| $ a_{c,y} = - f v_x $ |
implica que existe una corriente que se aleja de la costa. Esto genera una corriente que lleva aguas frías ricas en nutrientes a la superficie:
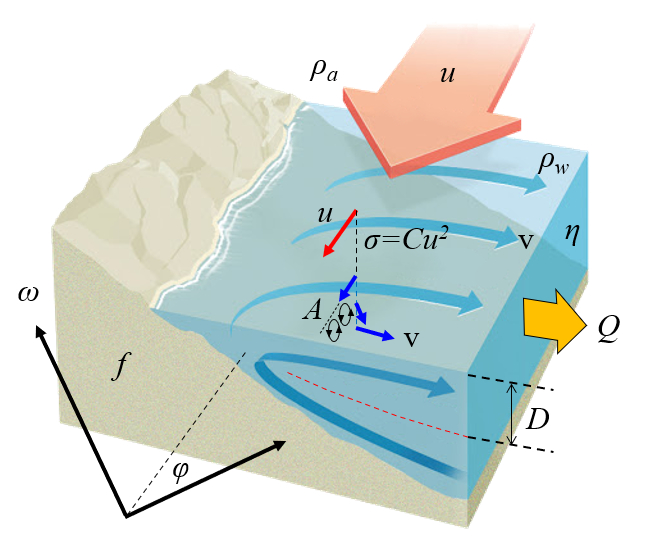
Este transporte se denomina el transporte de Ekman.
ID:(11679, 0)
Characterization of the ocean layers
Note 
Ekman's transport causes the boundaries between the surface and deepest layers in the ocean to shift. These are characterized by sudden changes in parameters depending on the temperature. In particular there are changes in:
• Temperature (thermocline)
• Salinity (halocline)
• Density (pycnocline)
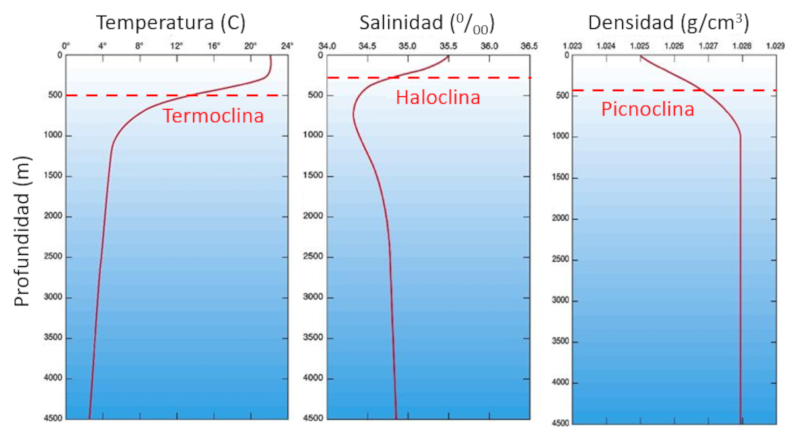
ID:(11684, 0)
Invers Ekman Transport
Quote 
Si se invierte el sentido del viento para el transporte de Ekman se tiene el proceso inverso (si
En este caso se tiene que con la velocidad hacia los polos resulta
| $ a_{c,y} = - f v_x $ |
Esto implica que existe una corriente que va hacia la costa evitando que los nutrientes lleguen a la superficie:
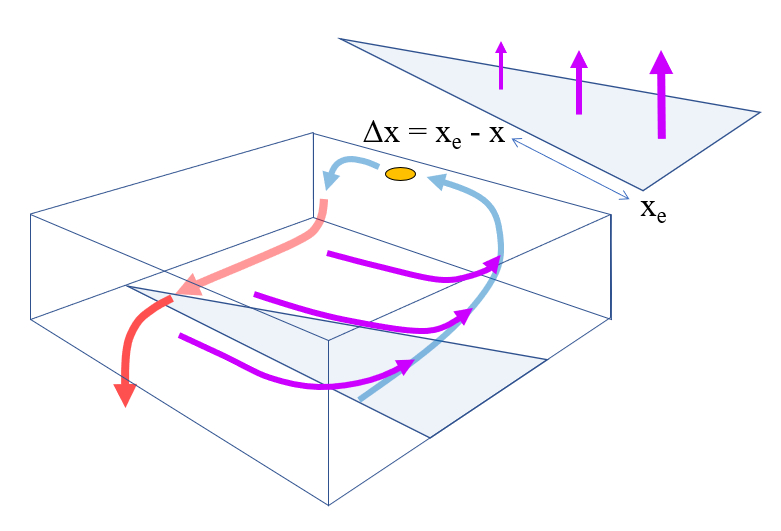
ID:(11680, 0)
Upwelling zones
Exercise 
Existen distintas zonas en el mundo en donde por vientos, ya sea en forma permanente o estacional, existe surgencia. Esto lleva a que en estos lugares las corrientes que van en dirección de la costa arrastran aguas frias ricas en vida en dirección de la superficie con lo que se favorece la vida en la superficie.
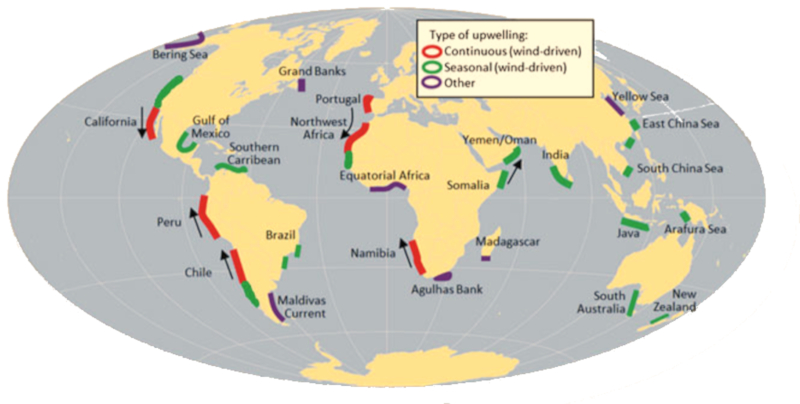
ID:(11700, 0)
Movement on coastal edges
Description 
At the shoreline, Coriolis force can lead to circulation that draws nutrient-rich material to the surface (Ekman transport).
Variables
Calculations
Calculations
Equations
With the wind-generated tension ($\tau_w$) over the surface $S$ of the ocean, a force is generated:
$F = \sigma_w S$
which acts upon the mass $m$ calculated from the sea water density ($\rho$), the ekman's Depth ($D_E$), and the surface $S$ through:
$m = \rho_w S D_E$
As the acceleration $a$ is generated by Coriolis with the ekman's speed ($u_e$):
$a = \displaystyle\frac{F}{m} =\displaystyle\frac{\sigma_w S}{\rho_w D_E S} = \displaystyle\frac{\sigma_w}{\rho_w D_E} = f u_e$
resulting in:
| $ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$ |
(ID 11701)
(ID 11702)
Examples
(ID 15446)
Cuando existen corrientes en direcci n del ecuador en los lados oeste en bordes continentales, la ecuaci n de Coriolis para el plano con
| $ a_{c,y} = - f v_x $ |
implica que existe una corriente que se aleja de la costa. Esto genera una corriente que lleva aguas fr as ricas en nutrientes a la superficie:

Este transporte se denomina el transporte de Ekman.
(ID 11679)
Ekman's transport causes the boundaries between the surface and deepest layers in the ocean to shift. These are characterized by sudden changes in parameters depending on the temperature. In particular there are changes in:
• Temperature (thermocline)
• Salinity (halocline)
• Density (pycnocline)

(ID 11684)
Si se invierte el sentido del viento para el transporte de Ekman se tiene el proceso inverso (si
En este caso se tiene que con la velocidad hacia los polos resulta
| $ a_{c,y} = - f v_x $ |
Esto implica que existe una corriente que va hacia la costa evitando que los nutrientes lleguen a la superficie:

(ID 11680)
Existen distintas zonas en el mundo en donde por vientos, ya sea en forma permanente o estacional, existe surgencia. Esto lleva a que en estos lugares las corrientes que van en direcci n de la costa arrastran aguas frias ricas en vida en direcci n de la superficie con lo que se favorece la vida en la superficie.

(ID 11700)
(ID 15443)
The energy density of the wind is a function of the air density ($\rho_a$) and the wind speed ($U$) in the form
$\displaystyle\frac{1}{2}\rho_aU^2$
If only a fraction of the energy is considered to be transferred, the wind-generated tension ($\tau_w$) can be modeled as the energy density multiplied by a factor the drag coefficient ($C_D$):
| $ \tau_w = \rho_a C_D U ^2$ |
(ID 11718)
The tension on the ocean surface generated by the wind is transmitted to the depths through vortices, which causes the dragging of the water mass. The depth of the water, or the ekman's Depth ($D_E$), that can be dragged, depends on how the energy diffuses to deeper layers, corresponding to the eddy viscosity for vertical mixing ($A_z$). It is, with the coriolis factor ($f$), equal to:
| $ D_E =\sqrt{\displaystyle\frac{2 \pi A_z }{ f }}$ |
(ID 11670)
The the wind-generated tension ($\tau_w$) generated by the wind leads to the surface velocity of the ocean, or the ekman's speed ($u_e$), which in turn, through the Coriolis force represented by the coriolis factor ($f$), generates the Ekman transport. This is, with the sea water density ($\rho$) and the ekman's Depth ($D_E$):
| $ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$ |
(ID 11701)
With the ekman's speed ($u_e$) and the ekman's Depth ($D_E$), the transported volume, or the ekman transport ($Q$), can be estimated:
| $ Q = D_E u_e $ |
(ID 11702)
ID:(1578, 0)
