Erdbewegungen
Storyboard 
Die Kraft der Sonne, die endlich einen Ort auf der Erde erreicht, hängt zum einen von der Entfernung zur Sonne, der Neigung der Achse und der Rotation des Planeten ab.
ID:(533, 0)
Elliptische Umlaufbahn
Definition 
Die Erdumlaufbahn bildet eine Ellipse, in der sich die Sonne in einem der Brennpunkte befindet:
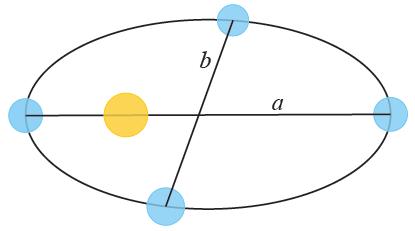
Die Ebene, die die Umlaufbahn enthält, wird Ekliptik genannt.
Der Punkt, der am weitesten von der Sonne entfernt ist, wird als Aphel bezeichnet (7. Juli), während der nächstgelegene Punkt Perihel (3. Januar) genannt wird. Die Zwischenpunkte, an denen die Erde den Punkt passiert, an dem der Radius mit der Halbachse zusammenfällt, werden als Sonnenwenden bezeichnet.
Die Radien werden als großer Halbachse (a) und kleiner Halbachse (b) bezeichnet.
Die Parameter der Umlaufbahn lauten wie folgt:
Parameter | Variable | Wert
|:---------------|:----------|:-----------:
Großer Halbachse (Semi-major axis) | $a$ | $149.598.000 km$
Kleiner Halbachse (Semi-minor axis) | $b$ | $149.577.000 km$
Aphel | | $152,1 \times 10^6 km$
Perihel | | $147,1 \times 10^6 km$
Exzentrizität der Umlaufbahn | $\epsilon$ | $0,0167$
Umlaufzeit | $T$ | $365,256 Tage$
Durchschnittsgeschwindigkeit | | $29.780 m/s$
ID:(3079, 0)
Art und Weise eine Ellipse zu bauen
Bild 
Eine Ellipse kann gezeichnet werden, indem man ein Schnur an zwei Punkten (den Brennpunkten) befestigt und die Schnur auf maximale Länge spannt. Anschließend werden mit einem Stift Punkte um beide Brennpunkte herum gezeichnet:
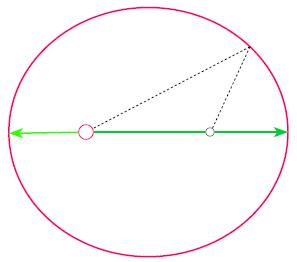
None
ID:(3081, 0)
Umlaufbahnkoordinaten
Notiz 
Die Position der Erde wird in Bezug auf die Koordinaten $(x, y)$ beschrieben, wobei der Mittelpunkt der Ellipse als Ursprung verwendet wird:
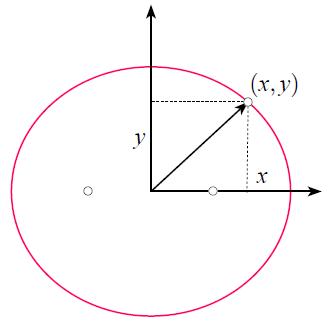
ID:(3080, 0)
Orbitale Exzentrizität
Zitat 
Da die Umlaufbahn eine Ellipse ist, weist sie einen gewissen Grad an Verformung auf, der mit der Exzentrizität gemessen wird.
Im Folgenden sind die Werte für verschiedene Planeten aufgeführt:
Planet | Exzentrizität [-]
|:-----------|:------------------:|
Merkur | 0,20563593
Venus | 0,00677672
Erde | 0,01671123
Mars | 0,0933941
Jupiter | 0,04838624
Saturn | 0,05386179
Uranus | 0,04725744
Neptun | 0,00859048
Quelle: NASA/Lunar and Planetary Institute
Daher haben nahezu alle Planeten eine annähernd kreisförmige Umlaufbahn.
ID:(3088, 0)
Neigung der Erdachse
Übung 
Die Achse der Erde hat eine Neigung von 23,5 Grad gegenüber der Ekliptik.
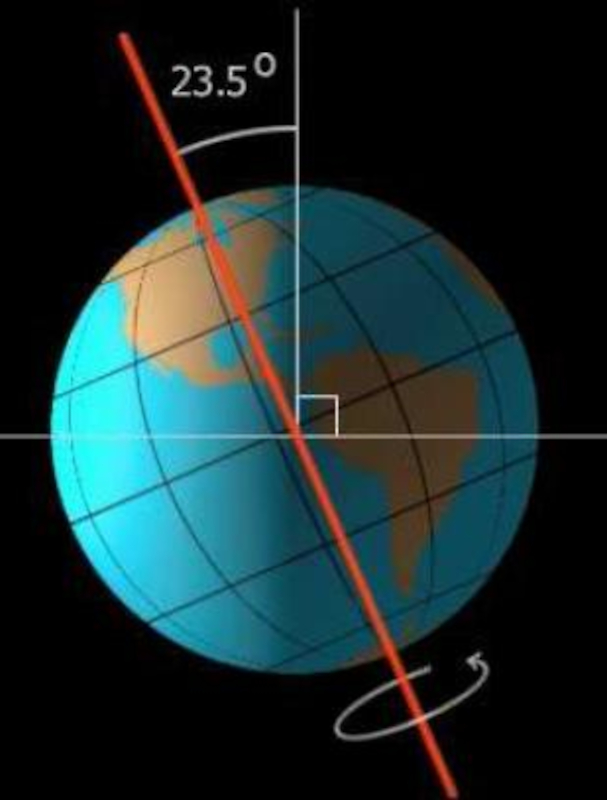
Die Neigung der Achse ist der Grund dafür, dass die Strahlung, die von jedem Hemisphären des Planeten empfangen wird, sich zwischen dem Moment, in dem der Planet im Perihel und Aphel ist, unterscheidet.
Die Werte für die Neigung verschiedener Planeten sind unten aufgeführt:
Planet | Neigung [Grad]
|:--------|:--------------------------:|
Merkur | 0
Venus | 177,3
Erde | 23,4393
Mars | 25,2
Jupiter | 3,1
Saturn | 26,7
Uranus | 97,8
Neptun | 28,3
Hinweis: Werte größer als 90 Grad entsprechen "rückläufigen Rotationen", d.h. Rotationen in entgegengesetzter Richtung.
Quelle: NASA/Lunar and Planetary Institute
ID:(3085, 0)
Erdbewegungen
Beschreibung 
Die Kraft der Sonne, die endlich einen Ort auf der Erde erreicht, hängt zum einen von der Entfernung zur Sonne, der Neigung der Achse und der Rotation des Planeten ab.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Die Erdumlaufbahn bildet eine Ellipse, in der sich die Sonne in einem der Brennpunkte befindet:

Die Ebene, die die Umlaufbahn enth lt, wird Ekliptik genannt.
Der Punkt, der am weitesten von der Sonne entfernt ist, wird als Aphel bezeichnet (7. Juli), w hrend der n chstgelegene Punkt Perihel (3. Januar) genannt wird. Die Zwischenpunkte, an denen die Erde den Punkt passiert, an dem der Radius mit der Halbachse zusammenf llt, werden als Sonnenwenden bezeichnet.
Die Radien werden als gro er Halbachse (a) und kleiner Halbachse (b) bezeichnet.
Die Parameter der Umlaufbahn lauten wie folgt:
Parameter | Variable | Wert
|:---------------|:----------|:-----------:
Gro er Halbachse (Semi-major axis) | $a$ | $149.598.000 km$
Kleiner Halbachse (Semi-minor axis) | $b$ | $149.577.000 km$
Aphel | | $152,1 \times 10^6 km$
Perihel | | $147,1 \times 10^6 km$
Exzentrizit t der Umlaufbahn | $\epsilon$ | $0,0167$
Umlaufzeit | $T$ | $365,256 Tage$
Durchschnittsgeschwindigkeit | | $29.780 m/s$
(ID 3079)
Eine Ellipse kann gezeichnet werden, indem man ein Schnur an zwei Punkten (den Brennpunkten) befestigt und die Schnur auf maximale L nge spannt. Anschlie end werden mit einem Stift Punkte um beide Brennpunkte herum gezeichnet:

None
(ID 3081)
Die Position der Erde wird in Bezug auf die Koordinaten $(x, y)$ beschrieben, wobei der Mittelpunkt der Ellipse als Ursprung verwendet wird:

(ID 3080)
Da die Umlaufbahn eine Ellipse ist, weist sie einen gewissen Grad an Verformung auf, der mit der Exzentrizit t gemessen wird.

Im Folgenden sind die Werte f r verschiedene Planeten aufgef hrt:
Planet | Exzentrizit t [-]
|:-----------|:------------------:|
Merkur | 0,20563593
Venus | 0,00677672
Erde | 0,01671123
Mars | 0,0933941
Jupiter | 0,04838624
Saturn | 0,05386179
Uranus | 0,04725744
Neptun | 0,00859048
Quelle: NASA/Lunar and Planetary Institute
Daher haben nahezu alle Planeten eine ann hernd kreisf rmige Umlaufbahn.
(ID 3088)
Die Achse der Erde hat eine Neigung von 23,5 Grad gegen ber der Ekliptik.

Die Neigung der Achse ist der Grund daf r, dass die Strahlung, die von jedem Hemisph ren des Planeten empfangen wird, sich zwischen dem Moment, in dem der Planet im Perihel und Aphel ist, unterscheidet.
Die Werte f r die Neigung verschiedener Planeten sind unten aufgef hrt:
Planet | Neigung [Grad]
|:--------|:--------------------------:|
Merkur | 0
Venus | 177,3
Erde | 23,4393
Mars | 25,2
Jupiter | 3,1
Saturn | 26,7
Uranus | 97,8
Neptun | 28,3
Hinweis: Werte gr er als 90 Grad entsprechen "r ckl ufigen Rotationen", d.h. Rotationen in entgegengesetzter Richtung.
Quelle: NASA/Lunar and Planetary Institute
(ID 3085)
Debido a la inclinaci n del eje terrestre la intensidad de luz solar varia durante el a o dependiendo de la posici n de la tierra en torno al sol.
(ID 6869)
ID:(533, 0)
