Utilisateur:
Pression sonore
Storyboard 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
La variation de l'impulsion $dp$ est associ e la masse des mol cules $m$ et la vitesse du son $u$ des mol cules travers :
$dp = 2mu \approx mu$
Ainsi, dans un intervalle de temps gal la p riode $dt \approx T$, nous avons :
$F=\displaystyle\frac{dp}{dt}=\displaystyle\frac{mu}{T}$
Par cons quent, a pression sonore ($p_s$) peut tre calcul en utilisant la pression
a concentration molaire ($c$) est
et le volume avec des molécules ($\Delta V$) qui varie
comme suit :
$p=\displaystyle\frac{1}{S} \displaystyle\frac{dp}{dt}=\displaystyle\frac{1}{S}\displaystyle\frac{mu}{T}=\displaystyle\frac{muc}{ScT}=\displaystyle\frac{muc}{S\lambda}=\displaystyle\frac{muc}{\Delta V}=\rho u c$
Dans le dernier terme, la fois le num rateur et le d nominateur sont multipli s par $c$. L'expression dans le d nominateur repr sente le volume du gaz d plac par le son en $T$, donc nous pouvons remplacer la masse divis e par ce volume par la densit , ce qui donne :
Puisque ERROR:5104 est calcul partir de a pression sonore ($p_s$) et a vitesse des molécules ($u$) en utilisant
ainsi que l'expression de a pression sonore ($p_s$) en termes de a densité moyenne ($\rho$) et a concentration molaire ($c$),
nous obtenons
Exemples
Lorsque le son se propage, il provoque le d placement des mol cules au bord du syst me, entra nant des impacts contre le mur. Ces impacts transf rent de l' lan au mur, ce qui se traduit par une force. Comme cette force est g n r e par un grand nombre de particules, son effet d pend de la surface du syst me, ce qui g n re une pression.
Il est important de comprendre que la pression sonore n'est pas gale la pression ambiante. Dans l'air, cette derni re est de l'ordre de $10^5,Pa$, tandis que la pression sonore est g n ralement bien inf rieure $1,Pa$.
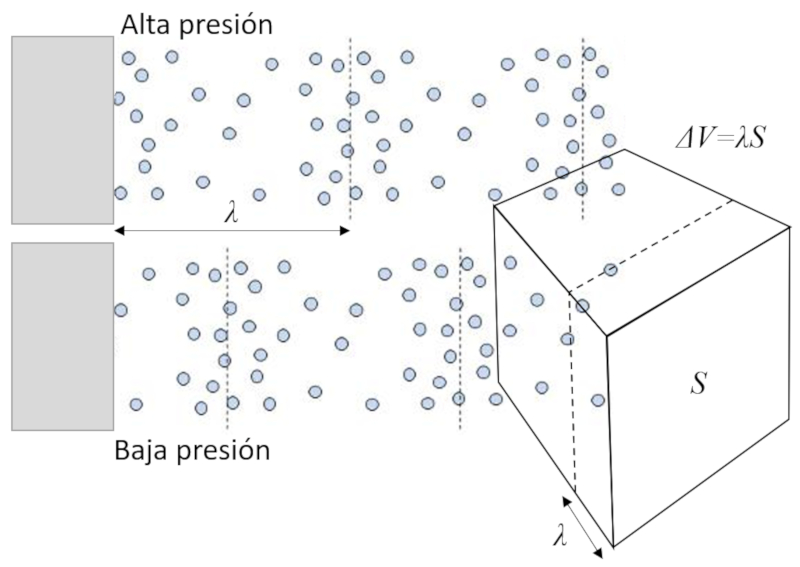
Si nous d pla ons la face d'un cube, nous g n rons une augmentation ou une diminution de la concentration, ce qui conduit une diminution ou une augmentation des collisions des mol cules avec la face du volume :
Comme la pression est le transfert de moment d aux collisions des mol cules avec la paroi, la variation du volume entra ne une augmentation ou une diminution de la pression.
A pression de la colonne d'eau ($p$) se calcule partir de a force de la colonne ($F$) et a hauteur de la colonne de liquide ($S$) comme suit :
Quand une onde sonore traverse un volume avec des molécules ($\Delta V$), elle se dilate et se contracte sur une distance de l'ordre de un longueur d'onde sonore ($\lambda$), ce qui entra ne une variation de volume d pendant de a coupe ou surface ($S$) perpendiculaire la direction de propagation.
Par cons quent, la variation de volume est gale :
A pression sonore ($p_s$) peut tre compris comme la densit de moment calcul e partir de a densité moyenne ($\rho$) et a vitesse des molécules ($u$), qui est ensuite multipli e par a concentration molaire ($c$) gr ce
A pression de référence ($L$) englobe une large gamme de a pression sonore ($p_s$), ce qui rend utile de d finir une chelle qui att nue cette difficult . Pour ce faire, nous pouvons travailler avec le logarithme de la pression normalis par une valeur correspondant z ro sur cette chelle. Si nous prenons la pression minimale qu'une personne peut d tecter, d finie comme a pression de référence ($p_{ref}$), nous pouvons d finir une chelle en utilisant :
qui commence 0 pour la plage audible. Dans le cas de l'air, a pression de référence ($p_{ref}$) est de $20 \mu Pa$.
Le concept de ERROR:5104,0 fournit une mesure de la r sistance du syst me transmettre l'onde sonore. Il prend en compte une pression agissante et tablit une mesure dans laquelle le milieu expos est d plac . Ainsi, a pression sonore ($p_s$) est compar a vitesse des molécules ($u$).
Par cons quent, ERROR:5104 est d fini comme :
Pour calculer ERROR:5104 partir de a densité moyenne ($\rho$) et a concentration molaire ($c$), on utilise la formule :
ID:(1589, 0)
