Benützer:
Gravitation
Storyboard 
Um zu beschreiben, wie sich die Geschwindigkeit im Laufe der Zeit entwickelt, muss der zeitliche Verlauf untersucht werden.
Das Geschwindigkeitsänderungsverhältnis entspricht der Krümmung des Weges in der verstrichenen Zeit, die geteilt durch diese der Beschleunigung entspricht.
Für eine endliche verstrichene Zeit entspricht die Geschwindigkeit der durchschnittlichen Beschleunigung während dieser Zeit.
ID:(1383, 0)
Schwerkraft Axis nach unten
Definition
Wenn ein Koordinatensystem verwendet wird, bei dem die positive z-Achse nach oben zeigt, entspricht die Gravitation einem Beschleunigungsprozess in Richtung nach unten:
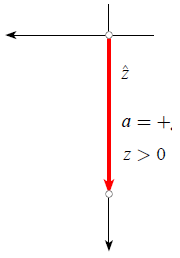
Schwerkraft mit nach unten weisender Achse
ID:(2249, 0)
Schwerkraft Axis nach oben
Bild
Wenn ein Koordinatensystem verwendet wird, bei dem die negative z-Achse nach unten zeigt, entspricht die Gravitation einem Beschleunigungsprozess in dieselbe Richtung wie die z-Achse:
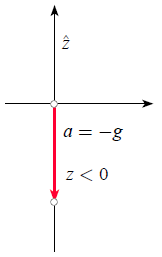
Schwerkraft mit nach oben zeigender Achse
ID:(2250, 0)
Gravitation
Storyboard
Um zu beschreiben, wie sich die Geschwindigkeit im Laufe der Zeit entwickelt, muss der zeitliche Verlauf untersucht werden. Das Geschwindigkeitsänderungsverhältnis entspricht der Krümmung des Weges in der verstrichenen Zeit, die geteilt durch diese der Beschleunigung entspricht. Für eine endliche verstrichene Zeit entspricht die Geschwindigkeit der durchschnittlichen Beschleunigung während dieser Zeit.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Beispiele
Wenn die Bewegung eines Objekts in einem Koordinatensystem beschrieben wird, bei dem die z-Achse nach oben (in Richtung Himmel) zeigt, ist die Beschleunigung, der das Objekt ausgesetzt ist, gleich der als negativ definierten Gravitationsbeschleunigung, gegeben durch
$a = -g < 0$
.
Da die Beschleunigung konstant ist, ndert sich die Geschwindigkeit des Objekts linear entsprechend der Gleichung
die in diesem Fall zu
vereinfacht wird.
Wenn ein Koordinatensystem verwendet wird, bei dem die positive z-Achse nach oben zeigt, entspricht die Gravitation einem Beschleunigungsprozess in Richtung nach unten:
Wenn ein Objekt in einem Koordinatensystem beschrieben wird, bei dem die z-Achse \"nach unten\" (Richtung Boden) zeigt, ist die Beschleunigung, der es ausgesetzt ist, gleich der Gravitationsbeschleunigung, die als positiv definiert ist:
$a = g > 0$
Da die Beschleunigung konstant ist, wird sich die Geschwindigkeit linear entwickeln, wie in der folgenden Gleichung dargestellt:
Daher kann sie in diesem Fall auf die folgende Gleichung reduziert werden:
Wenn ein Koordinatensystem verwendet wird, bei dem die negative z-Achse nach unten zeigt, entspricht die Gravitation einem Beschleunigungsprozess in dieselbe Richtung wie die z-Achse:
ID:(1383, 0)