Total kinetic energy
Storyboard 
The total kinetic energy is the sum of the kinetic energy of translation and the kinetic energy of rotation.
This distinction is important because depending on how an object moves, the kinetic energy can be distributed differently between translation and rotation, affecting the speed at which it moves.
ID:(1418, 0)
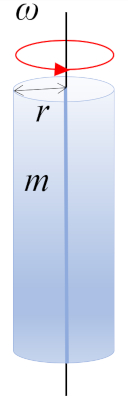
Cylinder rotating around axis $\parallel$
Image 
A rotation of a cylinder with mass $m$ and radius $r$ around the axis of the cylinder, where the center of mass (CM) is located at mid-height:
ID:(10964, 0)
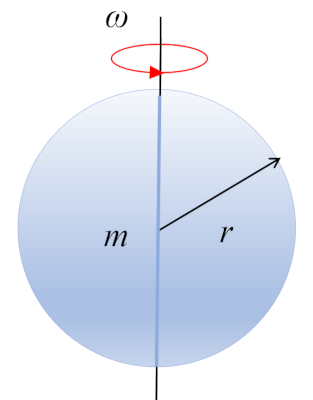
Sphere
Note 
A sphere with mass $m$ and radius $r$ is rotating around its center of mass, which is located at its geometric center:
ID:(10490, 0)
Total kinetic energy
Storyboard 
The total kinetic energy is the sum of the kinetic energy of translation and the kinetic energy of rotation. This distinction is important because depending on how an object moves, the kinetic energy can be distributed differently between translation and rotation, affecting the speed at which it moves.
Variables
Calculations
Calculations
Equations
The energy required for an object to change its angular velocity from $\omega_1$ to $\omega_2$ can be calculated using the definition
Applying Newton's second law, this expression can be rewritten as
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Using the definition of angular velocity
we get
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
The difference in angular velocities is
$\Delta\omega=\omega_2-\omega_1$
On the other hand, angular velocity itself can be approximated with the average angular velocity
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Using both expressions, we obtain the equation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Thus, the change in energy is given by
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
This allows us to define kinetic energy as
The work variance ($\Delta W$) required for an object to change from the initial Angular Speed ($\omega_0$) to the angular Speed ($\omega$) is obtained by applying a the torque ($T$) that produces an angular displacement the difference of Angles ($\Delta\theta$), according to:
Applying Newton's second law for rotation, in terms of the moment of inertia for axis that does not pass through the CM ($I$) and the mean Angular Acceleration ($\bar{\alpha}$):
this expression can be rewritten as:
$\Delta W = I \alpha \Delta\theta$
or, using the difference in Angular Speeds ($\Delta\omega$) and the time elapsed ($\Delta t$):
we get:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Using the definition of the mean angular velocity ($\bar{\omega}$) and the time elapsed ($\Delta t$):
results in:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
where the difference in Angular Speeds ($\Delta\omega$) is expressed as:
On the other hand, the angular velocity can be approximated by the average angular velocity:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
By combining both expressions, we obtain the equation:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Therefore, the change in energy is expressed as:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
This allows us to define the rotational kinetic energy as:
When an object rolls, its angular velocity is related to its translational velocity by
resulting in the rotational kinetic energy
which becomes
$K_r=\displaystyle\frac{1}{2}I \omega^2=\displaystyle\frac{1}{2} I \displaystyle\frac{v^2}{r^2}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{I}{r^2}\right)v^2$
Thus, when combining the translational kinetic energy
the kinetic energy of a rotating body is calculated by the sum
meaning,
The total Kinetic Energy ($K$) corresponds to the sum of the translational Kinetic Energy ($K_t$) and the kinetic energy of rotation ($K_r$):
Since the translational Kinetic Energy ($K_t$) is expressed as a function of the inertial Mass ($m_i$) and the speed ($v$):
and the kinetic energy of rotation ($K_r$), as a function of the moment of inertia for axis that does not pass through the CM ($I$) and the angular Speed ($\omega$), is defined as:
the final expression is:
Examples
The translational Kinetic Energy ($K_t$) is determined based on the speed ($v$) and the inertial Mass ($m_i$), according to:
5288 is associated with 6290 and not with 8762, even though they are numerically equal. The energy that an object possesses is a direct consequence of the inertia that had to be overcome to set it in motion.
The kinetic energy of rotation ($K_r$) is a function of the angular Speed ($\omega$) and of a measure of inertia represented by the moment of inertia for axis that does not pass through the CM ($I$):
The total Kinetic Energy ($K$) can have translational and/or rotational components. Therefore, it is expressed as the sum of the translational Kinetic Energy ($K_t$) and the kinetic energy of rotation ($K_r$):
The total kinetic energy is calculated by adding the kinetic energies of translation and rotation
so we have:
When an object rolls,
its angular velocity is related to its translational velocity by
resulting in the rotational kinetic energy
and consequently, yielding a total kinetic energy
ID:(1418, 0)
