Benützer:
RC-Schaltung
Definition 
El circuito RC es un circuito con una capacitancia y una resistencia tal como se ve en esta iamagen:
ID:(12071, 0)
Laden des Kondensators
Bild
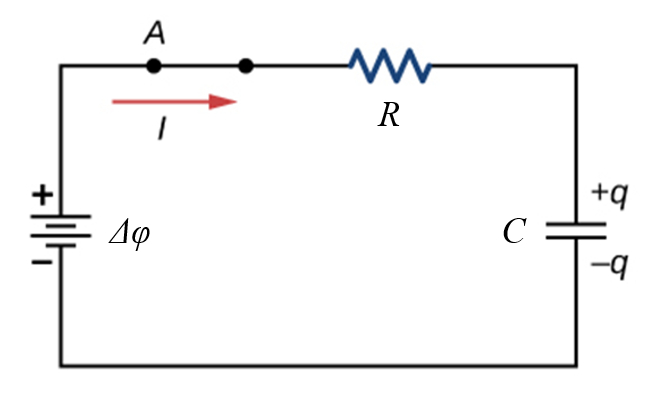
Cuando se conecta la batería al circuito se puede cargar el condensador:
ID:(12072, 0)
Entladen des Kondensators
Notiz
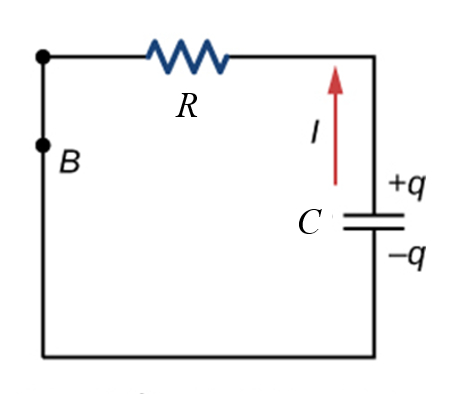
Cuando se cierra el circuito se puede descargar el condensador:
ID:(12073, 0)
Strom im Kondensator
Zitat
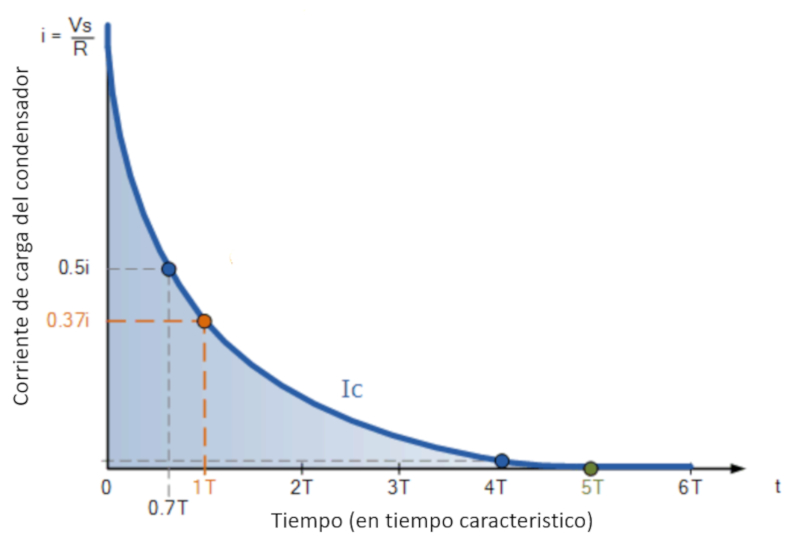
Cuando se cierra el circuito se puede descargar el condensador:
ID:(12075, 0)
Kondensatorpotenzial
Übung
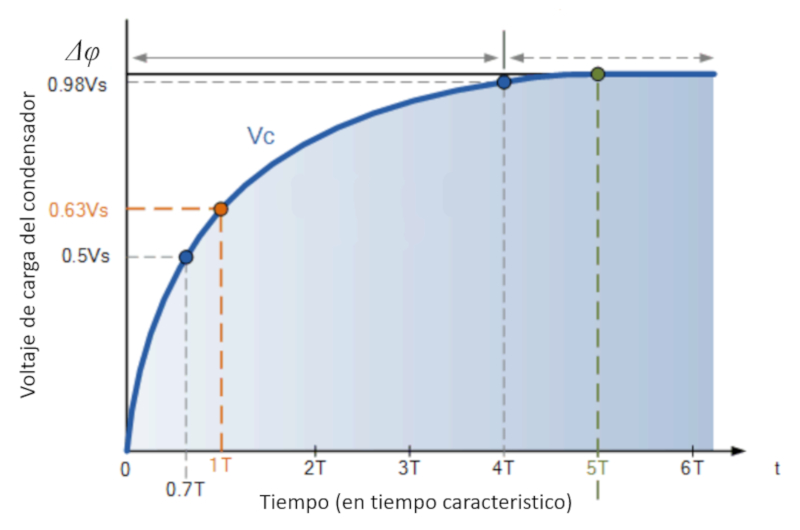
Cuando se cierra el circuito se puede descargar el condensador:
ID:(12074, 0)
RC-Schaltungen
Beschreibung
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Beispiele
El circuito RC es un circuito con una capacitancia y una resistencia tal como se ve en esta iamagen:
(ID 12071)
Cuando se conecta la bater a al circuito se puede cargar el condensador:
(ID 12072)
Cuando se cierra el circuito se puede descargar el condensador:
(ID 12073)
En el caso de carga se tiene que la segunda ley de Kirchhoff es con
| $- \Delta\varphi + R I + \Delta\varphi_C = 0$ |
(ID 12077)
A medida que las cargas van llegando al condensador se va formando el potencial que al final opondr a que nuevas cargas puedan lo contin en cargando.
Por ello el potencial del condensador ser con
| $ \Delta\varphi_C =\displaystyle\frac{1}{ C }\displaystyle\int_0^t I du $ |
(ID 12076)
Con la ecuaci n de la segunda ley de Kirchhoff, con potentialunterschied in der Kapazität $V$, potenzialunterschied an der Quelle $V$, strom $A$ und widerstand $Ohm$
| $- \Delta\varphi + R I + \Delta\varphi_C = 0$ |
y la ecuaci n del potencial del condensador, con
| $ \Delta\varphi_C =\displaystyle\frac{1}{ C }\displaystyle\int_0^t I du $ |
se llega reemplazando y derivando con potentialunterschied in der Kapazität $V$, potenzialunterschied an der Quelle $V$, strom $A$ und widerstand $Ohm$ a la ecuaci n
| $ R \displaystyle\frac{d I }{d t } + \displaystyle\frac{1}{ C } I = 0$ |
(ID 12080)
Con kondensatorkapazität $F$, potenzialunterschied an der Quelle $V$, strom $A$, widerstand $Ohm$ und zeit $s$ la ecuaci n para la corriente
| $ R \displaystyle\frac{d I }{d t } + \displaystyle\frac{1}{ C } I = 0$ |
y la condici n con potentialunterschied in der Kapazität $V$, potenzialunterschied an der Quelle $V$, strom $A$ und widerstand $Ohm$
| $- \Delta\varphi + R I + \Delta\varphi_C = 0$ |
que significa que inicialmente se tiene que
$I(0) = \displaystyle\frac{\Delta\varphi}{R}$
tiene la soluci n, con potentialunterschied in der Kapazität $V$, potenzialunterschied an der Quelle $V$, strom $A$ und widerstand $Ohm$, de la forma
| $ I =\displaystyle\frac{ \Delta\varphi }{ R } e^{- t / R C }$ |
(ID 12079)
Cuando se cierra el circuito se puede descargar el condensador:
(ID 12075)
Con la corriente calculada con kondensatorkapazität $F$, potenzialunterschied an der Quelle $V$, strom $A$, widerstand $Ohm$ und zeit $s$
| $ I =\displaystyle\frac{ \Delta\varphi }{ R } e^{- t / R C }$ |
y la relaci n de la segunda ley de Kirchhoff con potentialunterschied in der Kapazität $V$, potenzialunterschied an der Quelle $V$, strom $A$ und widerstand $Ohm$
| $- \Delta\varphi + R I + \Delta\varphi_C = 0$ |
se tiene con potentialunterschied in der Kapazität $V$, potenzialunterschied an der Quelle $V$, strom $A$ und widerstand $Ohm$ el potencial el ctrico en el condensador
| $ \Delta\varphi_C =\displaystyle\frac{ \Delta\varphi }{ R }(1-e^{- t / RC })$ |
(ID 12078)
Cuando se cierra el circuito se puede descargar el condensador:
(ID 12074)
ID:(1622, 0)