El ciclo consta de cuatro procesos reversibles: dos isot rmicos (temperatura constante) y dos adiab ticos (sin intercambio de calor). Durante la expansi n isot rmica, el sistema (t picamente un gas) absorbe calor de un reservorio de alta temperatura, expandi ndose y realizando trabajo sobre el entorno. Esto es seguido por una expansi n adiab tica donde el sistema contin a realizando trabajo pero sin intercambiar calor, lo que provoca que se enfr e. El gas luego experimenta una compresi n isot rmica, liberando calor a un reservorio m s fr o mientras se realiza trabajo sobre el gas para comprimirlo. El ciclo concluye con una compresi n adiab tica, que aumenta a n m s la temperatura del gas, devolvi ndolo a su estado original.

La belleza del ciclo de Carnot radica en su simplicidad y en la perspectiva que ofrece sobre los l mites de eficiencia para todos los motores basados en calor. La eficiencia de un motor de Carnot depende nicamente de las temperaturas de los reservorios caliente y fr o y es independiente de la sustancia de trabajo o los detalles del proceso en s . Esta eficiencia se expresa como la relaci n entre la diferencia de temperaturas entre los reservorios y la temperatura m s alta, mostrando que ning n motor real que opere entre dos reservorios de calor puede ser m s eficiente que un motor de Carnot operando entre los mismos reservorios.

mechanisms

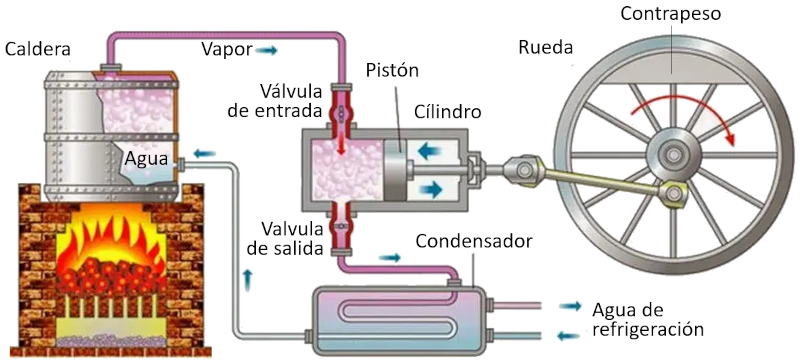
En una m quina que utiliza el concepto de Carnot, se llevan a cabo los siguientes procesos:

• El reservorio con la temperatura m s alta se crea mediante un horno.
• El reservorio con la temperatura m s baja se crea mediante un sistema de refrigeraci n.
• El vapor generado desde el reservorio se expande en forma de gas, desplazando el pist n y elevando la masa de compensaci n. En la primera etapa isot rmica, la primera v lvula est abierta mientras que la segunda est cerrada. En la segunda etapa del proceso, se cierra la primera v lvula y la expansi n contin a de manera adiab tica.
• En la tercera etapa, se abre la segunda v lvula y con ayuda de la masa de compensaci n, el pist n regresa y el gas es expulsado de forma isot rmica. En la cuarta etapa, se cierra la v lvula y el proceso concluye de manera adiab tica.

image

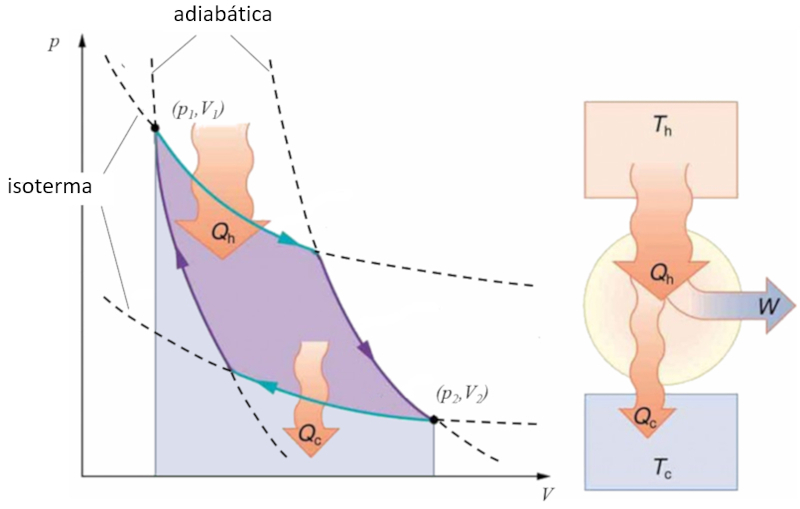
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:

image

The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.

Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work.

[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las m quinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)

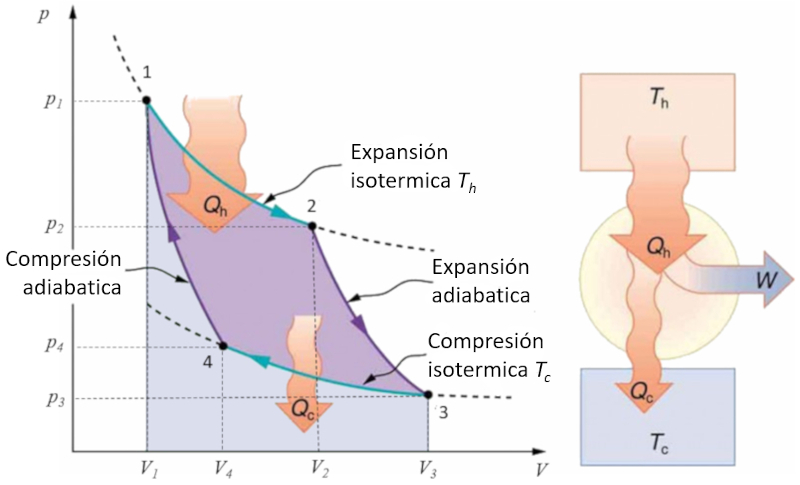
El ciclo de Carnot se describe de manera sencilla como un ciclo en el que se trabaja alternativamente de forma isot rmica y adiab tica. En particular, se estudian los diagramas de presi n-volumen y temperatura-entrop a. En el primer caso, se pueden identificar las cuatro etapas que se llevan a cabo:

Etapa 1 a 2: Expansi n isot rmica.
Etapa 2 a 3: Expansi n adiab tica.
Etapa 3 a 4: Compresi n isot rmica.
Etapa 4 a 1: Compresi n adiab tica.
Estas etapas se representan a continuaci n:

image

En el diagrama adjunto se muestra el flujo de energ a, donde el calor suministrado ($Q_H$) (caliente) sale del ba o a la temperatura alta ($T_H$), ingresa al sistema, se realiza un trabajo $W$, mientras que el complemento ERROR:8171,0 (fr o) es absorbido por el ba o a la temperatura baja ($T_C$).

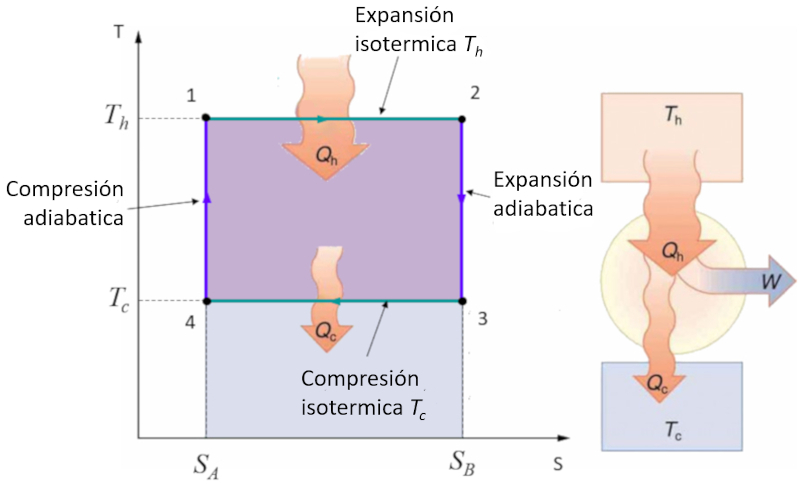
El ciclo de Carnot se describe de forma sencilla como un ciclo en el que se trabaja alternadamente de manera isot rmica y adiab tica. En particular, se estudian los diagramas de presi n-volumen y temperatura-entrop a. En el segundo caso, el diagrama se simplifica al pasar de etapas isot rmicas a etapas de entrop a constante:

En el diagrama temperatura-entrop a, las etapas de entrop a constante se representan de la siguiente manera:

image

Durante estas etapas, la entropía ($S$) se mantiene constante, lo que significa que no hay transferencia de calor, mientras que la temperatura absoluta ($T$) puede variar. Esto simplifica la representaci n del ciclo y facilita un an lisis m s directo de las propiedades termodin micas del sistema.

Dado que el diferencial inexacto del trabajo ($\delta W$) se define en funci n de la presión ($p$) y la variación del volumen ($\Delta V$) como:

equation=3468

Podemos calcular el trabajo efectivo ($W$) integrando a lo largo de las curvas del diagrama del ciclo:

$W = \displaystyle\oint pdV$

Utilizando la primera ley de la termodin mica con el diferencial de la energía interna ($dU$) y el diferencial inexacto del calor ($\delta Q$):

equation=9632

Y considerando el recorrido en el diagrama de la temperatura absoluta ($T$) y la entropía ($S$), obtenemos con la variación de la entropía ($dS$):

$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$

Dado que la integral a lo largo de un camino cerrado de un diferencial exacto es igual a cero, tenemos:

equation=11139

Teniendo en cuenta que la eficiencia ($\eta$) con el trabajo efectivo ($W$) y el calor suministrado ($Q_H$) es

equation=11154

puede ser sustituido por el trabajo efectivo ($W$) que junto a el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) resulta en

equation=11135

obteniendo la siguiente relaci n:

equation=11155

La eficiencia ($\eta$) es una funci n de el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) expresada como:

equation=11155

Podemos reemplazar el calor suministrado ($Q_H$) en funci n de la temperatura baja ($T_C$), la entropía baja ($S_C$) y la entropía alta ($S_H$) como:

equation=11138

Y utilizando la temperatura alta ($T_H$) como:

equation=11137

Si realizamos estos reemplazos, obtenemos:

equation=11136

model

Si en el ciclo de Carnot se extrae el calor suministrado ($Q_H$) del reservorio de mayor temperatura y se entrega el calor absorbido ($Q_C$) al reservorio de menor temperatura, se genera un trabajo efectivo ($W$) que es igual a:

kyon

El calor absorbido ($Q_C$) es igual a la temperatura baja ($T_C$) debido a la diferencia de entrop a, es decir, la entropía alta ($S_H$) y la entropía baja ($S_C$):

kyon

El calor suministrado ($Q_H$) es igual a la temperatura alta ($T_H$) debido a la diferencia de entrop a, es decir, la entropía alta ($S_H$) y la entropía baja ($S_C$):

kyon

La eficiencia ($\eta$) se puede definir como el porcentaje que representa el trabajo efectivo ($W$) en funci n de el calor suministrado ($Q_H$):

kyon.

La eficiencia ($\eta$) se puede calcular de el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) como

kyon

La eficiencia ($\eta$) se puede calcular en funci n de ERROR:8166,0 y ERROR:8167,0 con:

kyon