Arco-íris
Definição 
Se você observar um arco-íris, verá que na verdade são múltiplos arco-íris e que a sequência de cores se desloca: do azul ao vermelho e depois do vermelho ao azul, e assim por diante.

ID:(1844, 0)
O espectro
Imagem 
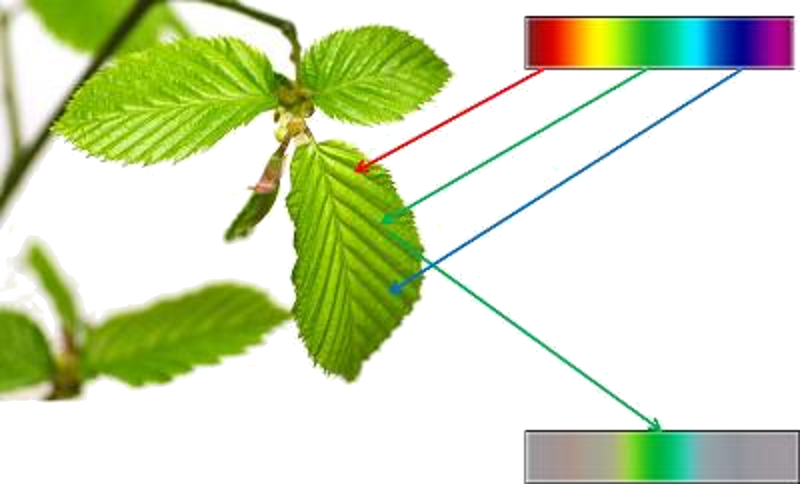
Uma vez que o ângulo de refração depende da frequência ou comprimento de onda da luz no vidro, é possível usar um prisma para decompor a luz em suas diferentes cores.

Isso resulta no que chamamos de espectro de luz.
ID:(6972, 0)
A luz e suas cores
Nota 
Um arco-íris nos mostra que a luz que o ilumina é decomposta em múltiplas cores. Na verdade, com uma observação cuidadosa, você pode ver que existem múltiplos arco-íris.
Isso acontece porque cada gota de água age como um pequeno prisma circular, permitindo múltiplas refrações e a criação de vários arco-íris.
ID:(1625, 0)
Espectro newtoniano
Citar 
Newton usou um prisma para decompor a luz em seus componentes, acreditando que poderia identificar um número finito de cores:

ID:(1682, 0)
Sir Isaac Newton
Exercício 
O primeiro a compreender a estrutura da luz como uma entidade física foi Sir Isaac Newton.
Sir Isaac Newton
(1643-1727)
Através de um experimento muito simples, ele demonstrou que a luz branca era composta por cores. No entanto, ele acreditava que o número de cores era discreto, como indicado em seu gráfico que representava suas observações.
ID:(6971, 0)
A realidade das coisas
Equação 
As cores que vemos nem sempre correspondem necessariamente à realidade. Nossos olhos captam a luz e geram impulsos elétricos com base na quantidade de luz azul, vermelha e verde que percebemos. No entanto, a intensidade nem sempre reflete as proporções reais, o que faz com que a percepção seja diferente da realidade:

ID:(12676, 0)
Luz e Cores
Storyboard 
Variáveis
Cálculos
Cálculos
Equações
Dado que o frequência de fotões ($\nu$) o inverso de o período ($T$):
$\nu=\displaystyle\frac{1}{T}$
isso significa que la superfície da fonte ($c$) igual dist ncia percorrida em uma oscila o, ou seja, ERROR:8439, dividida pelo tempo decorrido, que corresponde ao per odo:
$c=\displaystyle\frac{\lambda}{T}$
Em outras palavras, a seguinte rela o se aplica:
A energia de uma onda ou part cula (f ton) de luz definida como
Quando essa energia se propaga de um meio, por exemplo, um v cuo com velocidade da luz $c$, para outro meio com velocidade da luz $c_m$, conclui-se que a frequ ncia da luz permanece inalterada. No entanto, isso implica que, uma vez que a velocidade da luz igual ao produto da frequ ncia e do comprimento de onda, conforme expresso na equa o
o comprimento de onda deve mudar medida que transita entre meios.
Portanto, se tivermos um comprimento de onda da luz em um meio $\lambda_m$ e em um v cuo $\lambda$, o ndice de refra o pode ser definido como
e pode ser expresso como
$n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}$
Em outras palavras,
Exemplos
Se voc observar um arco- ris, ver que na verdade s o m ltiplos arco- ris e que a sequ ncia de cores se desloca: do azul ao vermelho e depois do vermelho ao azul, e assim por diante.
A cor da luz est associada sua o frequência de fotões ($\nu$), e existe uma rela o direta entre essa frequ ncia e la frequência de luz ($\epsilon$):
onde la constante de Planck ($h$) tem um valor de $6,62\times 10^{-34} , \text{Js}$.
Uma vez que o ngulo de refra o depende da frequ ncia ou comprimento de onda da luz no vidro, poss vel usar um prisma para decompor a luz em suas diferentes cores.
Isso resulta no que chamamos de espectro de luz.
O ndice de refra o, representado como $n$, definido como a raz o entre a velocidade da luz no v cuo, representada como $c$, e a velocidade da luz no meio, representada como $c_m$:
O f ton descrito como uma onda, e o frequência de fotões ($\nu$) est relacionada a ERROR:8439 atrav s de la superfície da fonte ($c$), de acordo com a seguinte f rmula:
Essa f rmula corresponde rela o mec nica que estabelece que a velocidade da onda igual ao comprimento de onda (dist ncia percorrida) dividido pelo per odo de oscila o, ou inversamente proporcional frequ ncia (o inverso do per odo).
Se $n$ for o ndice de refra o em um meio e $\lambda$ for o comprimento de onda no v cuo, ent o ao se propagar no meio, o comprimento de onda $\lambda_m$ ser
Um arco- ris nos mostra que a luz que o ilumina decomposta em m ltiplas cores. Na verdade, com uma observa o cuidadosa, voc pode ver que existem m ltiplos arco- ris.
Isso acontece porque cada gota de gua age como um pequeno prisma circular, permitindo m ltiplas refra es e a cria o de v rios arco- ris.
Newton usou um prisma para decompor a luz em seus componentes, acreditando que poderia identificar um n mero finito de cores:
O primeiro a compreender a estrutura da luz como uma entidade f sica foi Sir Isaac Newton.
Sir Isaac Newton
(1643-1727)
Atrav s de um experimento muito simples, ele demonstrou que a luz branca era composta por cores. No entanto, ele acreditava que o n mero de cores era discreto, como indicado em seu gr fico que representava suas observa es.
As cores que vemos nem sempre correspondem necessariamente realidade. Nossos olhos captam a luz e geram impulsos el tricos com base na quantidade de luz azul, vermelha e verde que percebemos. No entanto, a intensidade nem sempre reflete as propor es reais, o que faz com que a percep o seja diferente da realidade:
ID:(759, 0)
