Utilisateur:
Inertie de rotation
Définition 
Si nous considérons un objet ayant un moment d'inertie $I$ et une vitesse angulaire $\omega$, nous pouvons observer deux situations où il est plus difficile de changer son mouvement :
• Lorsque son moment d'inertie est très élevé (par exemple, essayer d'arrêter un carrousel).
• Lorsque sa vitesse angulaire est très élevée (par exemple, essayer d'arrêter l'axe d'un moteur).
C'est pourquoi une mesure du mouvement est introduite, qui implique le corps, à savoir le produit du moment d'inertie avec la vitesse angulaire, appelé moment cinétique du corps.
En danse classique, on peut voir comment la danseuse applique le premier principe de Newton pour la rotation dans toutes ses pirouettes :
ID:(10284, 0)
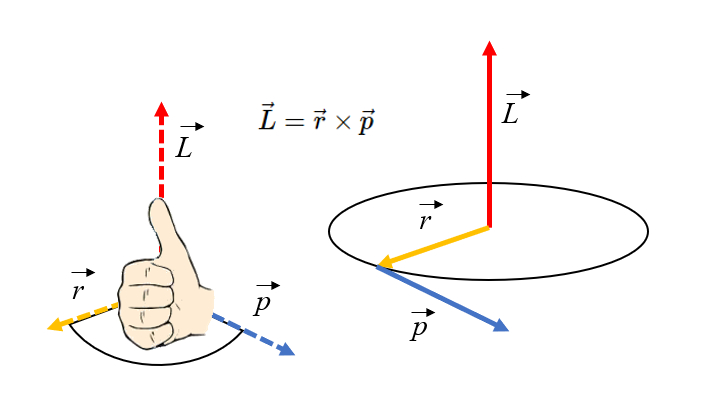
Moment angulaire, règle de la main droite
Image
L'orientation du moment angulaire peut être déterminée à l'aide de la règle de la main droite : si vous pointez vos doigts dans la direction du rayon et tournez dans la direction du moment,
ID:(11601, 0)
Inertie de rotation
Description
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
(ID 3251)
(ID 3251)
(ID 15841)
(ID 15842)
Exemples
(ID 15837)
Si nous consid rons un objet ayant un moment d'inertie $I$ et une vitesse angulaire $\omega$, nous pouvons observer deux situations o il est plus difficile de changer son mouvement :
• Lorsque son moment d'inertie est tr s lev (par exemple, essayer d'arr ter un carrousel).
• Lorsque sa vitesse angulaire est tr s lev e (par exemple, essayer d'arr ter l'axe d'un moteur).
C'est pourquoi une mesure du mouvement est introduite, qui implique le corps, savoir le produit du moment d'inertie avec la vitesse angulaire, appel moment cin tique du corps.
En danse classique, on peut voir comment la danseuse applique le premier principe de Newton pour la rotation dans toutes ses pirouettes :
(ID 10284)
(ID 15834)
Si le moment angulaire est constant, alors le moment cinétique ($L$) doit tre gal le moment cinétique initial ($L_0$), ce qui implique que :
| $ L = L_0 $ |
(ID 15841)
Le moment ($p$) a t d fini comme le produit de a masse d'inertie ($m_i$) et a vitesse ($v$), ce qui est gal :
| $ p = m_i v $ |
L'analogie de a vitesse ($v$) dans le cas de la rotation est a vitesse angulaire instantanée ($\omega$), donc l' quivalent de le moment ($p$) devrait tre un le moment cinétique ($L$) de la forme :
| $ L = I \omega $ |
.
a masse d'inertie ($m_i$) est associ l'inertie dans la translation d'un corps, donc le moment d'inertie ($I$) correspond l'inertie dans la rotation d'un corps.
(ID 3251)
Le moment ($p$) a t d fini comme le produit de a masse d'inertie ($m_i$) et a vitesse ($v$), ce qui est gal :
| $ p = m_i v $ |
L'analogie de a vitesse ($v$) dans le cas de la rotation est a vitesse angulaire instantanée ($\omega$), donc l' quivalent de le moment ($p$) devrait tre un le moment cinétique ($L$) de la forme :
| $ L = I \omega $ |
.
a masse d'inertie ($m_i$) est associ l'inertie dans la translation d'un corps, donc le moment d'inertie ($I$) correspond l'inertie dans la rotation d'un corps.
(ID 3251)
L'acc l ration est d finie comme le changement de vitesse angulaire par unit de temps.
Par cons quent, l'acc l ration angulaire a différence de vitesses angulaires ($\Delta\omega$) peut tre exprim e en termes de vitesse angulaire a vitesse angulaire ($\omega$) et de temps a vitesse angulaire initiale ($\omega_0$) comme suit :
| $ \Delta\omega = \omega_2 - \omega_1 $ |
(ID 3681)
Si la forme du corps change pendant la rotation, son moment d'inertie changera galement. Il est donc logique de d finir le variation du moment d'inertie ($\Delta I$) en soustrayant la valeur de a moment d\'inertie initial ($I_0$) de le moment d'inertie ($I$) comme suit :
| $ \Delta I = I - I_0 $ |
(ID 15842)
ID:(1455, 0)