Modelo de Hill
Storyboard 
Un modelo mas completo de como opera un musculo es el de Hill que considera tanto el comportamiento elástico que observamos en el caso de los saltos y amortización que se observo al final de dicho movimiento o que ocurre cuando vez que detenemos un pie al caminar.
ID:(1084, 0)
Estructura del modelo
Definición 
Hill propuso en 1938 un modelo que da cuenta de como se comporta mecánicamente un musculo que se puede reducir a resortes, amortiguadores y un motor que realiza la tracción:
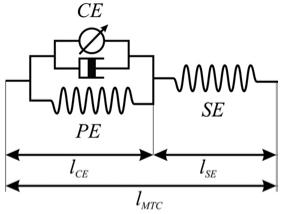
Modelo mecánico de Hill
Hoy en día entendemos que los distintos elementos tienen un equivalente biológico del musculo real. En dicha correspondencia se tiene que:
- el mecanismo de tracción corresponde a la actina, miosina y sarcomeros
- el resorte paralelo (PE) corresponde al tejido suave que envuelve el musculo
- el resorte serial (SE) los tendones mediante el musculo se liga al hueso
ID:(8767, 0)
Elemento serial: el tendón
Imagen 
La resistencia serial repersenta los tendones que conecta el musculo y el hueso.
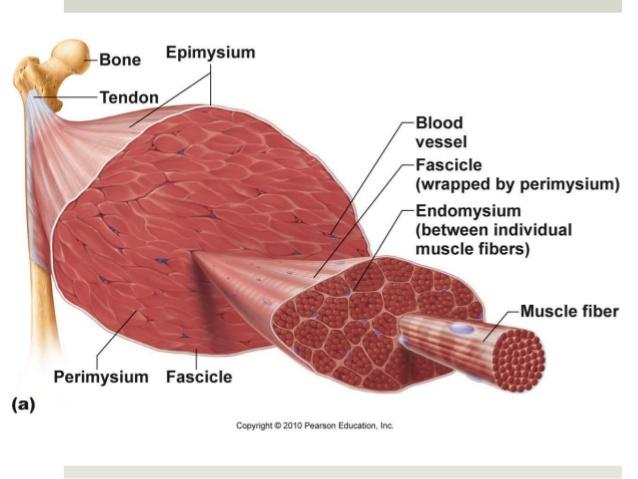
Estructura del músculo como sistema de fibras musculares en paralelo. Adicionalmente se muestra como el músculo esta fijado al hueso mediante tendones.
ID:(8768, 0)
Elemento motor: Actina-Miosina-Filamentos
Nota 
La estructura que impulsa el desplazamiento consta de las filamentos sobre las que se encuentran los bastones (miosina) y que enganchan sobre las cabezas (actina) en el filamento opuesto:
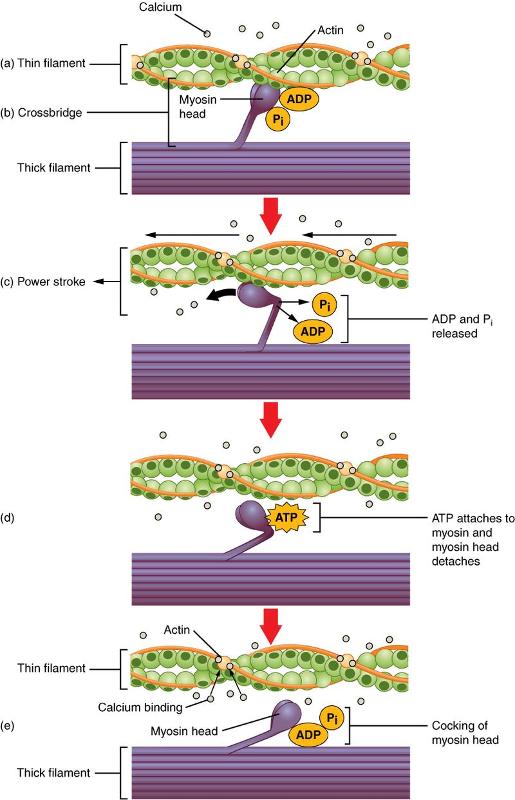
proceso en que el baston desplaza la actina, libera ADP y Pi, se adhiere ATP con lo que se libera la cabeza para luego reabsorber ADP y Pi e iniciar el proceso nuevamente.
ID:(8770, 0)
Equivalente para la parte motriz
Cita 
La imagen muestra como la actina (cabeza), miosina (brazo) y sarcomero (base) equivalen a la parte motriz del modelo de Hill:
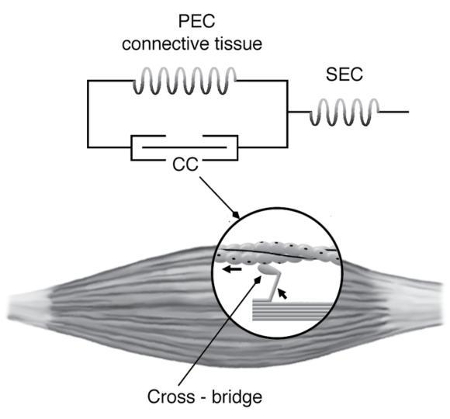
ID:(8780, 0)
Elemento paralelo: el tejido conectivo
Ejercicio 
El tejido que rodea las miofibrillas en el sarcomero y en las fibrillas conforman el sistema de tejido blando que actúa como un resorte paralelo a la parte motriz:
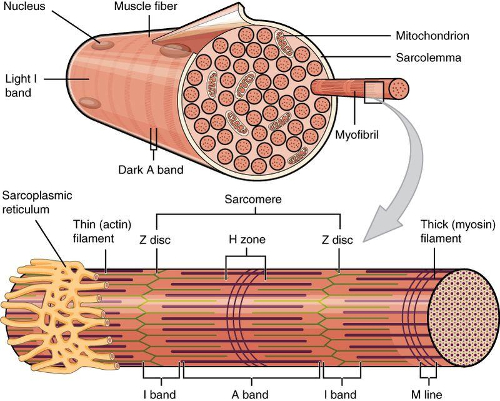
Estructura de la fibra muscular como múltiples miofibrillas en paralelo que a su vez están compuestas de múltiples sarcomeros en paralelo.
ID:(8769, 0)
Detalle de las curvas de fuerza y el modelo de Hill
Ecuación 
El modelo de Hill, aquí representado con un angulo entre la parte muscular y tendón:
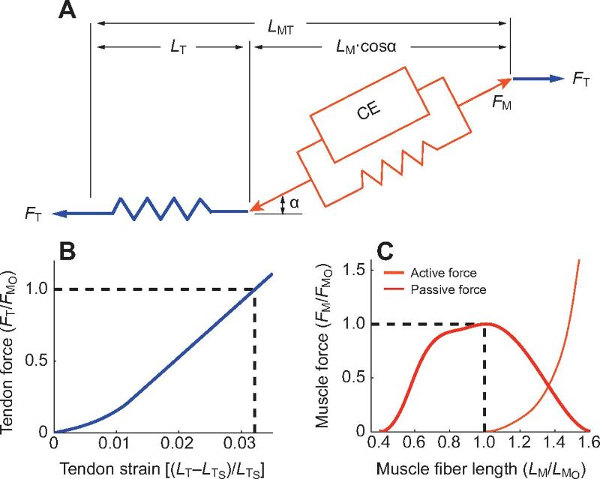
Diagrama de respuesta de los elementos del modelo de Hill
muestra ademas la gráfica de fuerza y dilatación del tendón (B).
La segunda gráfica (C) muestra la parte activa y pasiva. La primera corresponde al motor mientras que la segunda el resorte paralelo, que actúa en forma similar que el serial solo tras una deformación inicial.
ID:(8781, 0)
Detalle de la fuerza activa y pasiva
Script 
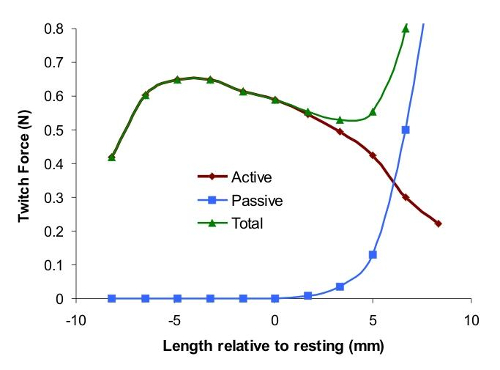
La siguiente gráfica muestra las curvas de fuerza activa y pasiva según y su suma:
ID:(8782, 0)
Modelo de Hill
Storyboard 
Un modelo mas completo de como opera un musculo es el de Hill que considera tanto el comportamiento elástico que observamos en el caso de los saltos y amortización que se observo al final de dicho movimiento o que ocurre cuando vez que detenemos un pie al caminar.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Hill propuso en 1938 un modelo que da cuenta de como se comporta mec nicamente un musculo que se puede reducir a resortes, amortiguadores y un motor que realiza la tracci n:
Hoy en d a entendemos que los distintos elementos tienen un equivalente biol gico del musculo real. En dicha correspondencia se tiene que:
- el mecanismo de tracci n corresponde a la actina, miosina y sarcomeros
- el resorte paralelo (PE) corresponde al tejido suave que envuelve el musculo
- el resorte serial (SE) los tendones mediante el musculo se liga al hueso
La resistencia serial repersenta los tendones que conecta el musculo y el hueso.
Para el tejido sano se asume que la variaci n de la fuerza tiene una componente el stica y una que depende de la fuerza misma:
Si se integra la ecuaci n del modelo del tend n:
se obtiene
donde la constante de integraci n debe ser elegida de modo que sin deformaci n (x=0) no exista fuerza.
Si se considera la fuerza del modelo del tend n:
en la aproximaci n de
donde el camino
La estructura que impulsa el desplazamiento consta de las filamentos sobre las que se encuentran los bastones (miosina) y que enganchan sobre las cabezas (actina) en el filamento opuesto:
La imagen muestra como la actina (cabeza), miosina (brazo) y sarcomero (base) equivalen a la parte motriz del modelo de Hill:
El modelo de amortiguaci n general es de la forma
En muchos casos se asume que el exponente es del orden de uno.
En el caso del elemento motriz, el amortiguaci n y el resorte paralelos la ecuaci n tiene un elemento que genera fuerza en el tiempo
y el termino el stico
se da
El factor
El largo total del sistema es igual a la suma del elemento amrotiguador
Si el sistema solo funciona con el elemento de amortiguaci n el largo se reduce a un largo
La fuerza total se calcula como la suma del elemento de amortiguaci n
Con la relaci n del resorte serial
y la definici n del largo total
se tiene que la ecuaci n para el musculo
se puede escribir como:
de lo que se puede despejar la derivada de la fuerza en el tiempo quedando:
Hill propone para describir el elemento activo una ecuaci n que liga la fuerza
donde
La ecuaci n de Hill implica que:
- al ser alta la fuerza la velocidad de contracci n debe ser baja
- con alta velocidad de contracci n solo se pueden lograr peque as fuerzas
El tejido que rodea las miofibrillas en el sarcomero y en las fibrillas conforman el sistema de tejido blando que act a como un resorte paralelo a la parte motriz:
El modelo de Hill, aqu representado con un angulo entre la parte muscular y tend n:
muestra ademas la gr fica de fuerza y dilataci n del tend n (B).
La segunda gr fica (C) muestra la parte activa y pasiva. La primera corresponde al motor mientras que la segunda el resorte paralelo, que act a en forma similar que el serial solo tras una deformaci n inicial.
La siguiente gr fica muestra las curvas de fuerza activa y pasiva seg n y su suma:
En el caso de que el sistema es en paralelo las fuerzas son iguales:
El factor
donde
ID:(1084, 0)
