Storyboard

Se considera una columna con agua con un orificio en su parte inferior. El vaciado es monitoreado obteniendo una velocidad de salida en función de la altura de la columna.Si los datos se modelan con Bernoulli pero la salida por el orificio se modela con Hagen Poiseville con lo que se logra corregir el problema del caso en que se asumio sin viscosidad.

>Modelo

ID:(1428, 0)

Concepto

ID:(15492, 0)

Descripción

Si dejamos caer una pequeña esfera de radio $a$ en un medio con viscosidad $\eta$, esta experimentará una aceleración hasta que la fuerza gravitacional,

$mg=\displaystyle\frac{4\pi}{3}a^3\rho_sg$

donde $\rho_s$ es la densidad del material de la esfera, se iguale a la fuerza viscosa,

$6\pi \eta a v$

siendo $v$ la velocidad de la esfera.

De esta manera, es posible estimar la viscosidad del medio midiendo la velocidad, ya que se cumple la ecuación:

$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$

En esta imagen se puede apreciar el comportamiento de la esfera:

ID:(9871, 0)

Descripción

Esto significa que a medida que la columna se va vaciando y la altura $h$ se reduce, la velocidad $v$ también disminuye de manera proporcional.

ID:(9870, 0)

Descripción

Si analizamos la ecuación

que describe la aplicación de Hagen-Poiseuille, se observa que la curva solo coincide con los datos experimentales en los siguientes casos:

La velocidad es baja (cuando la columna está casi vacía).

El radio del canal de evacuación debe reducirse de 1,5 mm a 0,6 mm.

Esto muestra que el flujo es principalmente turbulento y que solo a niveles de baja velocidad la velocidad es lo suficientemente baja como para que el número de Reynolds sea bajo y el flujo sea laminar.

ID:(11065, 0)

Imagen

Si observamos el recorrido que realiza la bolita en el tiempo, podemos notar que en gran medida se desplaza a una velocidad constante de aproximadamente 0,31 metros en 25 segundos, es decir, 0,0124 m/s.

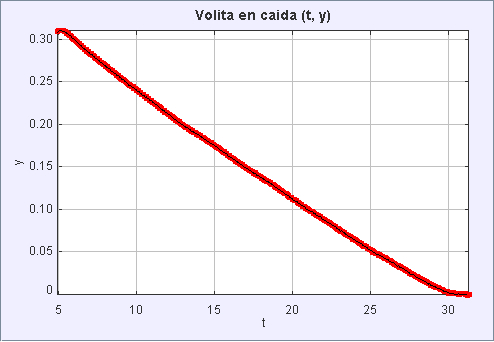
Despejando la igualdad entre la fuerza gravitacional y la fuerza de resistencia de Stokes:

$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$

obtenemos que:

$\eta = \displaystyle\frac{2 a^2\rho_sg}{9 v}$

Considerando que la bolita tiene un radio de 2 mm y pesa 8 mg, podemos calcular que su densidad es aproximadamente $\rho_s\sim 2,38 g/cm^3$. Por lo tanto, la viscosidad resultante es aproximadamente $\eta\sim 1,67 Pa s$.

ID:(9881, 0)

Concepto

ID:(15494, 0)

Descripción

Consideremos el sistema de un cubo cilíndrico con un agujero de evacuación. Al retirar el tapón, el agua comienza a fluir en función de la presión existente. Según Bernoulli en el interior ($v\sim 0$), la velocidad es nula y tenemos:

$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$

mientras que en el exterior ($h=0$), solo existe la componente cinética:

$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$

Como ambas expresiones son iguales, tenemos:

$\displaystyle\frac{1}{2}\rho v^2=\rho g h$

por lo que la velocidad es:

$v=\sqrt{2 g h}$

Para comparar con el experimento, podemos utilizar esta expresión para estimar con:

el alcance que debería tener el chorro. Si lo representamos gráficamente, observamos:

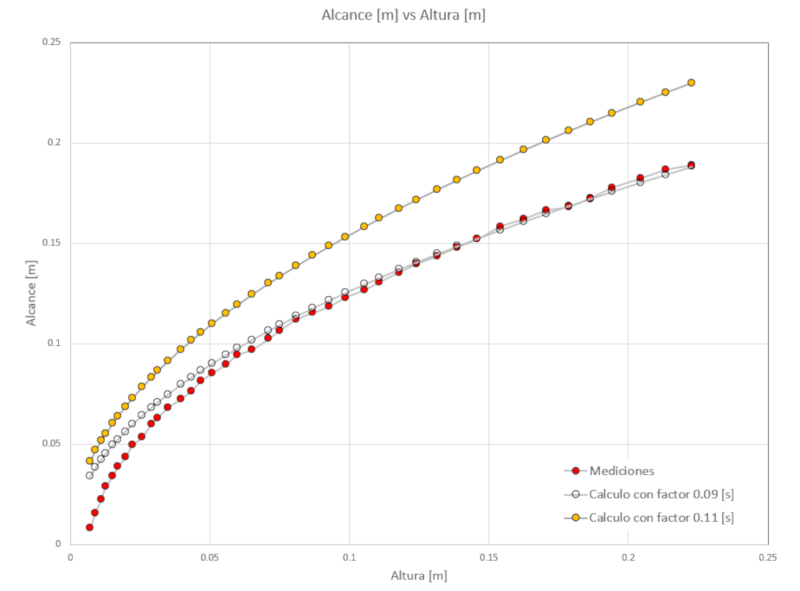
donde:• los puntos rojos corresponden a las mediciones experimentales,• los puntos azules corresponden al alcance calculado utilizando un factor de 0.11,• los puntos transparentes corresponden al alcance calculado utilizando un factor de 0.09.Por lo tanto, podemos concluir que el modelo de Bernoulli sobreestima la velocidad a la que se vacía el cubo. Esto se debe a que en la zona del agujero de evacuación, los efectos de la viscosidad no son despreciables y, por lo tanto, la velocidad es menor.

ID:(11063, 0)