Druyd:Knowledge

Aceleração angular constante, dois estágios

Storyboard

No caso de um movimento angular acelerado em duas etapas, no momento em que se passa da primeira para a segunda aceleração angular, a velocidade angular final da primeira etapa se torna a velocidade angular inicial da segunda. O mesmo ocorre com o ângulo, onde o ângulo final da primeira etapa é igual ao ângulo inicial da segunda etapa.Ao contrário do modelo de duas velocidades angulares, este modelo não apresenta problemas de descontinuidade, exceto que a aceleração angular pode mudar de forma abrupta, o que é tecnicamente possível, embora muitas vezes não seja muito realista.

>Modelo

ID:(1409, 0)

Mecanismos

Conceito

ID:(15413, 0)

Movimento em dois estágios

Descrição

Em um cenário de movimento em duas etapas, inicialmente o objeto ajusta sua velocidade pela diferença de la variação das velocidades angulares no primeiro estágio ( $\Delta\omega_1$ ) durante um período de o tempo decorrido na primeira etapa ( $\Delta t_1$ ), experimentando uma aceleração de la aceleração angular durante o primeiro estágio ( $\alpha_1$ ).

$\alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$

Na segunda etapa, o objeto continua modificando sua velocidade por la variação das velocidades angulares no segundo estágio ( $\Delta\omega_2$ ) ao longo de um intervalo de tempo o tempo gasto na segunda etapa ( $\Delta t_2$ ), com uma aceleração de la aceleração angular durante o segundo estágio ( $\alpha_2$ ).

$\alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$

Ao visualizar isso graficamente, obtém-se um diagrama de velocidade versus tempo como mostrado abaixo:

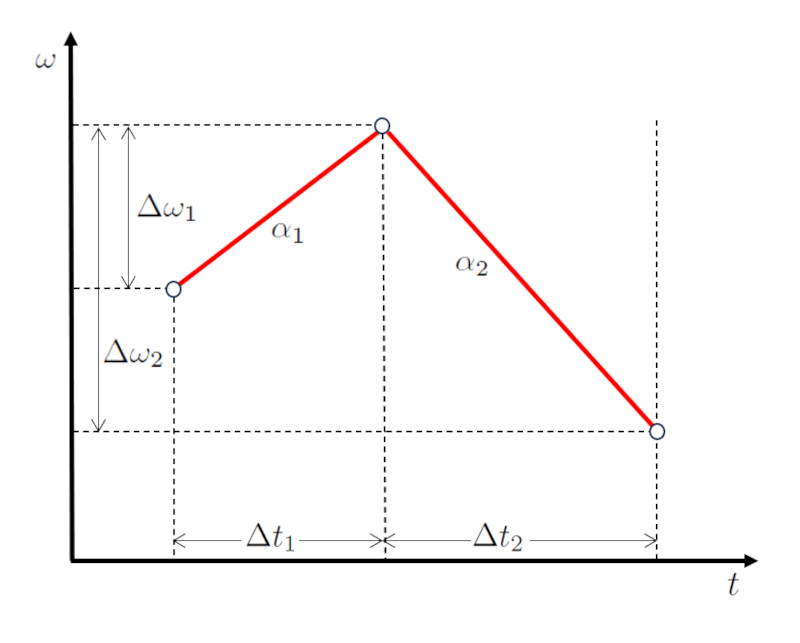
É importante notar que os intervalos de tempo o tempo decorrido na primeira etapa ( $\Delta t_1$ ) e o tempo gasto na segunda etapa ( $\Delta t_2$ ) são sequenciais, assim como as diferenças de velocidade la variação das velocidades angulares no primeiro estágio ( $\Delta\omega_1$ ) e la variação das velocidades angulares no segundo estágio ( $\Delta\omega_2$ ).

ID:(12521, 0)

Velocidade angular em um movimento de dois estágios

Descrição

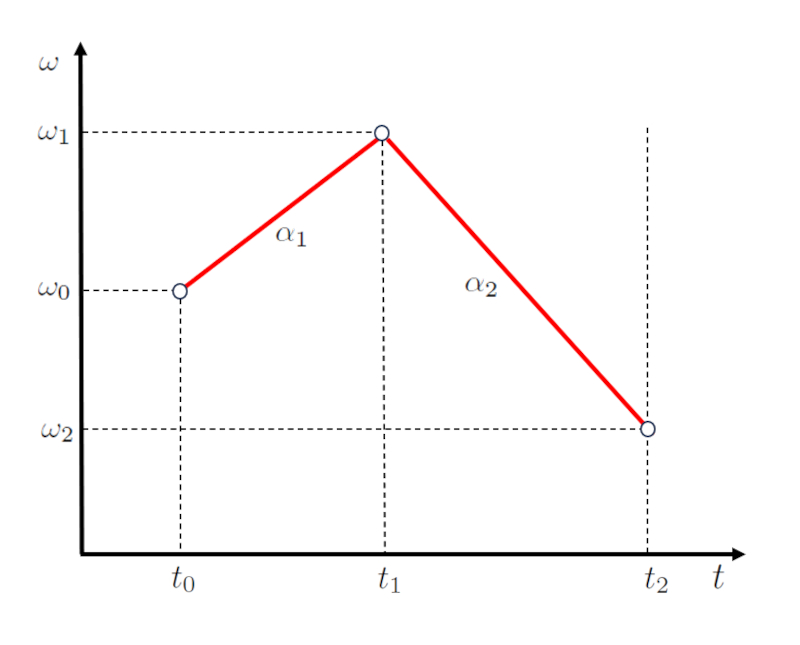
Na análise de um movimento segmentado em duas etapas, a primeira fase é caracterizada por uma função linear que incorpora os pontos o tempo inicial ( $t_0$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ), la velocidade angular inicial ( $\omega_0$ ) e la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ). Esta é expressa através de uma linha com inclinação de la aceleração angular durante o primeiro estágio ( $\alpha_1$ ), cuja relação matemática é especificada na seguinte equação:

$\omega_1 = \omega_0 + \alpha_1 ( t_1 - t_0 )$

Na transição para a segunda etapa, que é definida pelos pontos la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ), la velocidade angular final do segundo estágio ( $\omega_2$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ) e o hora de término da segunda etapa ( $t_2$ ), adota-se uma nova função linear com uma inclinação de la aceleração angular durante o segundo estágio ( $\alpha_2$ ). Esta relação é delineada pela segunda equação apresentada:

$\omega_2 = \omega_1 + \alpha_2 ( t_2 - t_1 )$

A representação gráfica destas relações lineares é ilustrada abaixo, fornecendo uma visualização clara de como a inclinação varia entre as duas etapas:

ID:(12522, 0)

Ângulo em um movimento de dois estágios

Descrição

Em um cenário de movimento dividido em duas etapas, o ângulo no final da primeira etapa é o mesmo que o ângulo no início da segunda etapa, designado como o primeiro ângulo final e segunda etapa começaram ( $\theta_1$ ).

Da mesma forma, o momento em que a primeira etapa termina coincide com o início da segunda etapa, marcado por o tempo final da primeira e início da segunda etapa ( $t_1$ ).

Dado que o movimento é definido pela aceleração angular experimentada, a velocidade angular no final da primeira etapa deve coincidir com a velocidade angular inicial da segunda etapa, indicada por la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ).

No contexto de uma aceleração angular constante, o ângulo em o primeiro ângulo final e segunda etapa começaram ( $\theta_1$ ) é determinado pelas variáveis o ângulo inicial ( $\theta_0$ ), la velocidade angular inicial ( $\omega_0$ ), la aceleração angular durante o primeiro estágio ( $\alpha_1$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ) e o tempo inicial ( $t_0$ ), conforme mostrado na seguinte equação:

$\theta_1 = \theta_0 + \omega_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} \alpha_1 ( t_1 - t_0 )^2$

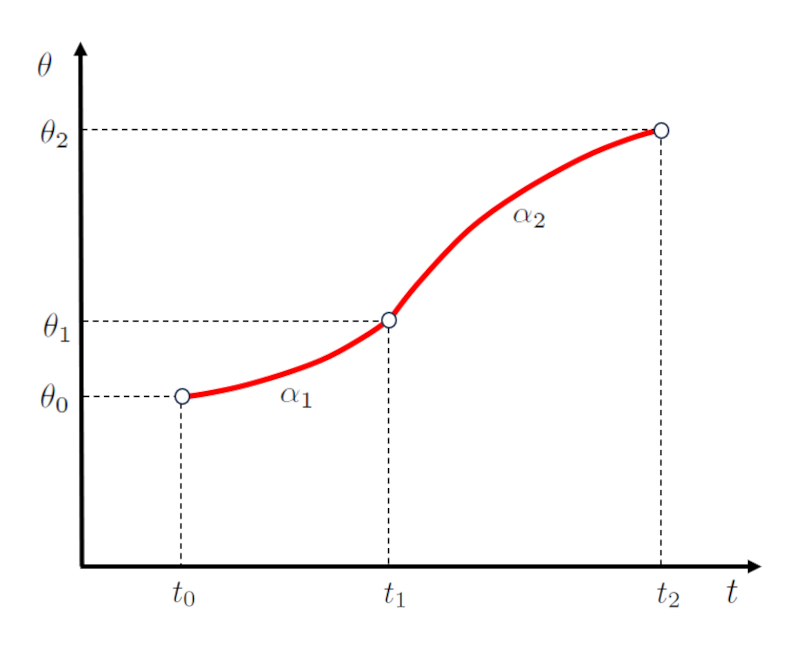
Na segunda etapa, o ângulo em la ângulo final do segundo estágio ( $\theta_2$ ) é calculado com base em o primeiro ângulo final e segunda etapa começaram ( $\theta_1$ ), la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ), la aceleração angular durante o segundo estágio ( $\alpha_2$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ) e o hora de término da segunda etapa ( $t_2$ ), de acordo com:

$\theta_2 = \theta_1 + \omega_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} \alpha_2 ( t_2 - t_1 )^2$

A representação gráfica dessas relações é ilustrada abaixo:

ID:(12520, 0)

Modelo

Conceito

ID:(15424, 0)

Aceleração angular constante, dois estágios

Modelo

No caso de um movimento angular acelerado em duas etapas, no momento em que se passa da primeira para a segunda aceleração angular, a velocidade angular final da primeira etapa se torna a velocidade angular inicial da segunda. O mesmo ocorre com o ângulo, onde o ângulo final da primeira etapa é igual ao ângulo inicial da segunda etapa. Ao contrário do modelo de duas velocidades angulares, este modelo não apresenta problemas de descontinuidade, exceto que a aceleração angular pode mudar de forma abrupta, o que é tecnicamente possível, embora muitas vezes não seja muito realista.

Variáveis

Símbolo

Texto

Variáve

Valor

Unidades

Calcular

Valeur MKS

Unidades MKS

$\alpha_1$

alpha_1

Aceleração angular durante o primeiro estágio

rad/s^2

$\alpha_2$

alpha_2

Aceleração angular durante o segundo estágio

rad/s^2

$a_1$

a_1

Aceleração durante a primeira fase

m/s^2

$a_2$

a_2

Aceleração durante a segunda etapa

m/s^2

$\theta_2$

theta_2

Ângulo final do segundo estágio

rad

$\theta_0$

theta_0

ângulo inicial

rad

$\Delta\theta$

Dtheta

Diferença de ângulos

rad

$t_2$

t_2

Hora de término da segunda etapa

$\omega_1$

omega_1

Primeira velocidade angular final e início do segundo estágio

rad/s

$\theta_1$

theta_1

Primeiro ângulo final e segunda etapa começaram

rad

$r$

Rádio

$\Delta t_1$

Dt_1

Tempo decorrido na primeira etapa

$t_1$

t_1

Tempo final da primeira e início da segunda etapa

$\Delta t_2$

Dt_2

Tempo gasto na segunda etapa

$t_0$

t_0

Tempo inicial

$\Delta\omega_1$

Domega_1

Variação das velocidades angulares no primeiro estágio

rad/s

$\Delta\omega_2$

Domega_2

Variação das velocidades angulares no segundo estágio

rad/s

$\omega_2$

omega_2

Velocidade angular final do segundo estágio

rad/s

$\omega_0$

omega_0

Velocidade angular inicial

rad/s

Cálculos

Equação

Primeiro, selecione a equação:

para

, depois, selecione a variável:

para

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve

Dado

Calcular

Objetivo :

Equação

A ser usado

Equações

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

alpha_m = Domega / Dt

A defini o da acelera o angular m dia baseada no ngulo percorrido

$\Delta\omega = \omega_2 - \omega_1$

e no tempo decorrido

$\Delta t \equiv t - t_0$

A rela o entre os dois definida como a acelera o angular m dia

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

dentro desse intervalo de tempo.

(ID 3234)

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

alpha_m = Domega / Dt

A defini o da acelera o angular m dia baseada no ngulo percorrido

$\Delta\omega = \omega_2 - \omega_1$

e no tempo decorrido

$\Delta t \equiv t - t_0$

A rela o entre os dois definida como a acelera o angular m dia

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

dentro desse intervalo de tempo.

(ID 3234)

$a = r \alpha$

a = r * alpha

Dado que la aceleração média ( $\bar{a}$ ) igual a la diferença de velocidade ( $\Delta v$ ) e o tempo decorrido ( $\Delta t$ ) conforme

$\bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$

e la aceleração angular média ( $\bar{\alpha}$ ) igual a la diferença de velocidades angulares ( $\Delta\omega$ ) e o tempo decorrido ( $\Delta t$ ) conforme

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

deduz-se que

$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$

Assumindo que la aceleração angular média ( $\bar{\alpha}$ ) igual a la aceleração angular constante ( $\alpha_0$ )

$\bar{\alpha} = \alpha_0$

e supondo que la aceleração média ( $\bar{a}$ ) igual a la aceleração constante ( $a_0$ )

$a_0 = \bar{a}$

obt m-se a seguinte equa o:

$a = r \alpha$

(ID 3236)

$a = r \alpha$

a = r * alpha

Dado que la aceleração média ( $\bar{a}$ ) igual a la diferença de velocidade ( $\Delta v$ ) e o tempo decorrido ( $\Delta t$ ) conforme

$\bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$

e la aceleração angular média ( $\bar{\alpha}$ ) igual a la diferença de velocidades angulares ( $\Delta\omega$ ) e o tempo decorrido ( $\Delta t$ ) conforme

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

deduz-se que

$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$

Assumindo que la aceleração angular média ( $\bar{\alpha}$ ) igual a la aceleração angular constante ( $\alpha_0$ )

$\bar{\alpha} = \alpha_0$

e supondo que la aceleração média ( $\bar{a}$ ) igual a la aceleração constante ( $a_0$ )

$a_0 = \bar{a}$

obt m-se a seguinte equa o:

$a = r \alpha$

(ID 3236)

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

omega = omega_0 + alpha_0 * ( t - t_0 )

Se assumirmos que la aceleração angular média ( $\bar{\alpha}$ ) constante, equivalente a la aceleração angular constante ( $\alpha_0$ ), ent o a seguinte equa o se aplica:

$\bar{\alpha} = \alpha_0$

Portanto, considerando la diferença de velocidades angulares ( $\Delta\omega$ ) junto com la velocidade angular ( $\omega$ ) e la velocidade angular inicial ( $\omega_0$ ):

$\Delta\omega = \omega_2 - \omega_1$

e o tempo decorrido ( $\Delta t$ ) em rela o a o tempo ( $t$ ) e o tempo inicial ( $t_0$ ):

$\Delta t \equiv t - t_0$

a equa o para la aceleração angular média ( $\bar{\alpha}$ ):

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

pode ser expressa como:

$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$

Resolvendo isso, obtemos:

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

(ID 3237)

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

omega = omega_0 + alpha_0 * ( t - t_0 )

Se assumirmos que la aceleração angular média ( $\bar{\alpha}$ ) constante, equivalente a la aceleração angular constante ( $\alpha_0$ ), ent o a seguinte equa o se aplica:

$\bar{\alpha} = \alpha_0$

Portanto, considerando la diferença de velocidades angulares ( $\Delta\omega$ ) junto com la velocidade angular ( $\omega$ ) e la velocidade angular inicial ( $\omega_0$ ):

$\Delta\omega = \omega_2 - \omega_1$

e o tempo decorrido ( $\Delta t$ ) em rela o a o tempo ( $t$ ) e o tempo inicial ( $t_0$ ):

$\Delta t \equiv t - t_0$

a equa o para la aceleração angular média ( $\bar{\alpha}$ ):

$\bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$

pode ser expressa como:

$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$

Resolvendo isso, obtemos:

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

(ID 3237)

$\Delta\theta = \theta_2 - \theta_1$

Dtheta = theta - theta_0

(ID 3680)

$\Delta\theta = \theta_2 - \theta_1$

Dtheta = theta - theta_0

(ID 3680)

$\Delta\omega = \omega_2 - \omega_1$

Domega = omega_2 - omega_1

(ID 3681)

$\Delta\omega = \omega_2 - \omega_1$

Domega = omega_2 - omega_1

(ID 3681)

$\theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$

theta = theta_0 + omega_0 *( t - t_0 )+ alpha_0 *( t - t_0 )^2/2

No caso de la aceleração angular constante ( $\alpha_0$ ), la velocidade angular ( $\omega$ ) como fun o de o tempo ( $t$ ) segue uma rela o linear com o tempo inicial ( $t_0$ ) e la velocidade angular inicial ( $\omega_0$ ) na forma:

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

Dado que o deslocamento angular igual rea sob a curva de velocidade angular-tempo, neste caso, pode-se adicionar as contribui es do ret ngulo:

$\omega_0(t-t_0)$

e do tri ngulo:

$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$

Isso nos leva express o para o ângulo ( $\theta$ ) e o ângulo inicial ( $\theta_0$ ):

$\theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$

(ID 3682)

$\theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$

theta = theta_0 + omega_0 *( t - t_0 )+ alpha_0 *( t - t_0 )^2/2

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

Dado que o deslocamento angular igual rea sob a curva de velocidade angular-tempo, neste caso, pode-se adicionar as contribui es do ret ngulo:

$\omega_0(t-t_0)$

e do tri ngulo:

$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$

Isso nos leva express o para o ângulo ( $\theta$ ) e o ângulo inicial ( $\theta_0$ ):

$\theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$

(ID 3682)

$\Delta t \equiv t - t_0$

Dt = t - t_0

(ID 4353)

$\Delta t \equiv t - t_0$

Dt = t - t_0

(ID 4353)

$\theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$

theta = theta_0 +( omega ^2 - omega_0 ^2)/(2* alpha_0 )

Se resolvermos o tempo na equa o de la velocidade angular ( $\omega$ ) que inclui as vari veis la velocidade angular inicial ( $\omega_0$ ), o tempo ( $t$ ), o tempo inicial ( $t_0$ ) e la aceleração angular constante ( $\alpha_0$ ):

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

obtemos a seguinte express o para o tempo:

$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$

Esta solu o pode ser substitu da na equa o para calcular o ângulo ( $\theta$ ) usando o ângulo inicial ( $\theta_0$ ) da seguinte forma:

$\theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$

o que resulta na seguinte equa o:

$\theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$

(ID 4386)

$\theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$

theta = theta_0 +( omega ^2 - omega_0 ^2)/(2* alpha_0 )

$\omega = \omega_0 + \alpha_0 ( t - t_0 )$

obtemos a seguinte express o para o tempo:

$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$

Esta solu o pode ser substitu da na equa o para calcular o ângulo ( $\theta$ ) usando o ângulo inicial ( $\theta_0$ ) da seguinte forma:

$\theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$

o que resulta na seguinte equa o:

$\theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$

(ID 4386)

Exemplos

Mecanismos

(ID 15413)

Movimento em dois est gios

Em um cen rio de movimento em duas etapas, inicialmente o objeto ajusta sua velocidade pela diferen a de la variação das velocidades angulares no primeiro estágio ( $\Delta\omega_1$ ) durante um per odo de o tempo decorrido na primeira etapa ( $\Delta t_1$ ), experimentando uma acelera o de la aceleração angular durante o primeiro estágio ( $\alpha_1$ ).

$\alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$

Na segunda etapa, o objeto continua modificando sua velocidade por la variação das velocidades angulares no segundo estágio ( $\Delta\omega_2$ ) ao longo de um intervalo de tempo o tempo gasto na segunda etapa ( $\Delta t_2$ ), com uma acelera o de la aceleração angular durante o segundo estágio ( $\alpha_2$ ).

$\alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$

Ao visualizar isso graficamente, obt m-se um diagrama de velocidade versus tempo como mostrado abaixo:

importante notar que os intervalos de tempo o tempo decorrido na primeira etapa ( $\Delta t_1$ ) e o tempo gasto na segunda etapa ( $\Delta t_2$ ) s o sequenciais, assim como as diferen as de velocidade la variação das velocidades angulares no primeiro estágio ( $\Delta\omega_1$ ) e la variação das velocidades angulares no segundo estágio ( $\Delta\omega_2$ ).

(ID 12521)

Velocidade angular em um movimento de dois est gios

Na an lise de um movimento segmentado em duas etapas, a primeira fase caracterizada por uma fun o linear que incorpora os pontos o tempo inicial ( $t_0$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ), la velocidade angular inicial ( $\omega_0$ ) e la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ). Esta expressa atrav s de uma linha com inclina o de la aceleração angular durante o primeiro estágio ( $\alpha_1$ ), cuja rela o matem tica especificada na seguinte equa o:

$\omega_1 = \omega_0 + \alpha_1 ( t_1 - t_0 )$

Na transi o para a segunda etapa, que definida pelos pontos la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ), la velocidade angular final do segundo estágio ( $\omega_2$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ) e o hora de término da segunda etapa ( $t_2$ ), adota-se uma nova fun o linear com uma inclina o de la aceleração angular durante o segundo estágio ( $\alpha_2$ ). Esta rela o delineada pela segunda equa o apresentada:

$\omega_2 = \omega_1 + \alpha_2 ( t_2 - t_1 )$

A representa o gr fica destas rela es lineares ilustrada abaixo, fornecendo uma visualiza o clara de como a inclina o varia entre as duas etapas:

(ID 12522)

ngulo em um movimento de dois est gios

Em um cen rio de movimento dividido em duas etapas, o ngulo no final da primeira etapa o mesmo que o ngulo no in cio da segunda etapa, designado como o primeiro ângulo final e segunda etapa começaram ( $\theta_1$ ).

Da mesma forma, o momento em que a primeira etapa termina coincide com o in cio da segunda etapa, marcado por o tempo final da primeira e início da segunda etapa ( $t_1$ ).

Dado que o movimento definido pela acelera o angular experimentada, a velocidade angular no final da primeira etapa deve coincidir com a velocidade angular inicial da segunda etapa, indicada por la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ).

No contexto de uma acelera o angular constante, o ngulo em o primeiro ângulo final e segunda etapa começaram ( $\theta_1$ ) determinado pelas vari veis o ângulo inicial ( $\theta_0$ ), la velocidade angular inicial ( $\omega_0$ ), la aceleração angular durante o primeiro estágio ( $\alpha_1$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ) e o tempo inicial ( $t_0$ ), conforme mostrado na seguinte equa o:

$\theta_1 = \theta_0 + \omega_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} \alpha_1 ( t_1 - t_0 )^2$

Na segunda etapa, o ngulo em la ângulo final do segundo estágio ( $\theta_2$ ) calculado com base em o primeiro ângulo final e segunda etapa começaram ( $\theta_1$ ), la primeira velocidade angular final e início do segundo estágio ( $\omega_1$ ), la aceleração angular durante o segundo estágio ( $\alpha_2$ ), o tempo final da primeira e início da segunda etapa ( $t_1$ ) e o hora de término da segunda etapa ( $t_2$ ), de acordo com:

$\theta_2 = \theta_1 + \omega_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} \alpha_2 ( t_2 - t_1 )^2$

A representa o gr fica dessas rela es ilustrada abaixo:

(ID 12520)

Modelo

(ID 15424)

ID:(1409, 0)