Posición en una dimensión
Storyboard 
Para determinar la posición de un objeto, se introduce un sistema de coordenadas que permite establecer un punto de origen y definir la posición mediante la medición de la distancia a lo largo de una línea recta o una curva. Por tanto, la unidad de posición corresponde a una longitud, como kilómetros, metros, centímetros, y así sucesivamente.La elección del sistema de coordenadas es flexible y se busca con el propósito de simplificar al máximo la modelación y los cálculos asociados. Por ejemplo, si el objeto se desplaza a lo largo de una vía, que no necesariamente es recta, es conveniente definir el sistema de coordenadas a lo largo de esa vía. En este caso particular, la posición se define como la distancia desde el origen o el punto de inicio de la vía.
ID:(607, 0)
Posición, una dimensión
Simulation 
Uno de los aspectos fundamentales de la física es determinar la posición de los objetos que analizamos. Este simulador permite explorar ese concepto: al generar una barra roja y desplazar el mouse, se puede determinar su longitud. Dicha longitud corresponde a la posición de su borde derecho respecto a un origen situado en el borde izquierdo.
Medición del tamaño de la caja roja
Crea una caja roja presionando el botón ubicado debajo de la regla. Luego, arrástrala manteniendo pulsado el botón izquierdo del mouse hasta alinear el cero con el borde izquierdo de la caja. Lee el valor que aparece en el borde derecho, ingrésalo en el casillero inferior y presiona el botón para verificar si la medición es correcta.Considere el panel del simulador:
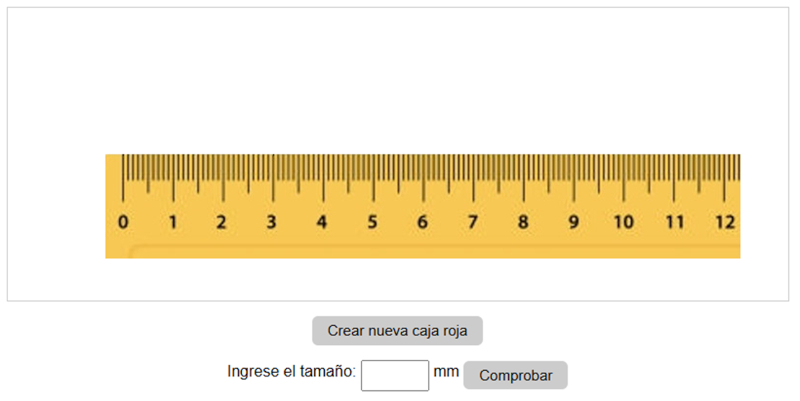
Cree una caja roja presionando el botón que se encuentra debajo de la regla.
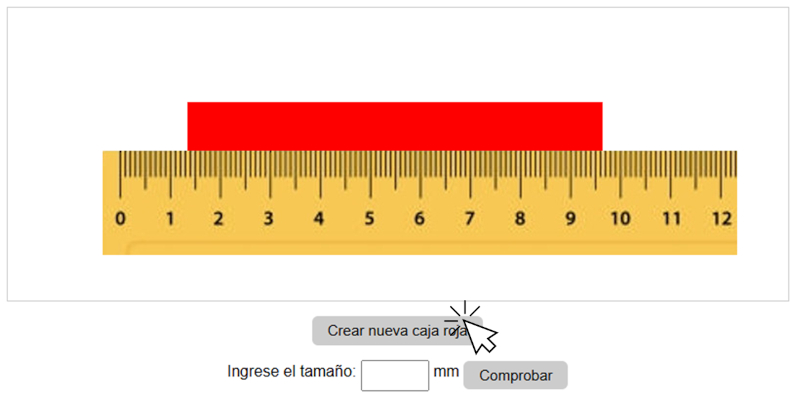
Luego, arrástrela manteniendo presionado el botón izquierdo del mouse.
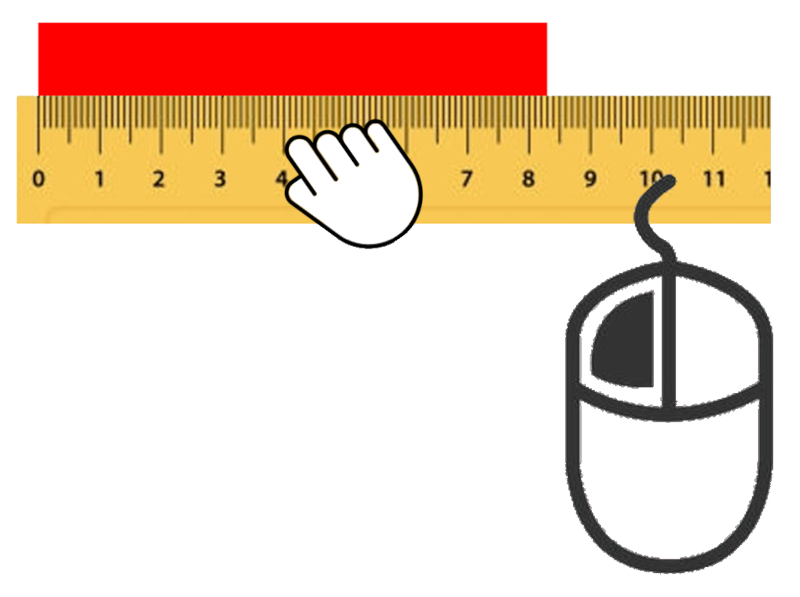
Asegúrese de que quede correctamente alineada con el cero de la regla en el borde izquierdo de la caja.

Lea el valor que aparece en el borde derecho.

Ingrese el valor estimado en el casillero inferior (puede ingresar también valores fraccionarios).

Si el valor es correcto, se lo confirmará. En caso de error, se le mostrará el valor correcto.
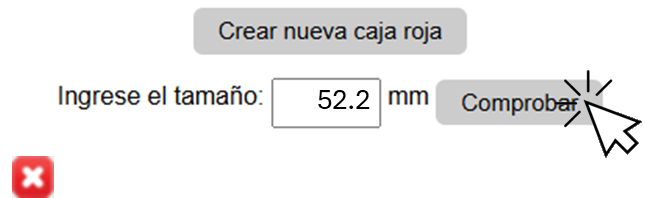
Puede experimentar desplazando el origen hacia la izquierda y observar cómo un pequeño error en la alineación inicial genera una diferencia en el resultado final. También puede modificar el valor ingresado: se considerará correcto siempre que se encuentre dentro de un margen de un milímetro.
Si alguien nos dice que su ubicación es 45 km, inmediatamente surge la necesidad de preguntar: ¿desde dónde? Es decir, necesitamos conocer el origen que da sentido a esa información.
En el simulador, esto se traduce en la necesidad de colocar el cero de la regla en el borde izquierdo de la caja roja para poder determinar correctamente la posición del borde derecho.

Si no se posiciona cuidadosamente, el valor que leamos en la regla en el borde derecho será incorrecto, y la simulación nos mostrará que hemos medido mal:

Al colocar la regla en el origen, notamos de inmediato que resulta difícil hacer coincidir exactamente el cero con el borde izquierdo. Algo similar ocurre en el borde derecho, donde este cae entre dos marcas de la regla, y nos vemos obligados a estimar a qué valor corresponde:

Finalmente, procedemos a estimar el porcentaje del espacio entre las dos líneas y terminamos asignando una décima de milímetro como valor. Sin embargo, esto nos hace darnos cuenta de que estamos operando a nivel de décimas de milímetro, sin siquiera considerar las centésimas.
Por lo tanto, concluimos que todo instrumento de medición (no solo los que miden longitud) posee una limitación inherente. Por esta razón, los valores obtenidos en una medición deben expresarse siempre junto con su incertidumbre. Esto puede indicarse asociando el número a un rango, por ejemplo: [27.1, 27.7], o bien utilizando el valor medio (27.4) y señalando cuánto debe sumarse o restarse para cubrir el rango:
27.4±0.3
Esta práctica no solo se aplica a cada medición individual, sino también al cálculo de distancias, como se ilustra en el modelo mediante un ejemplo.
ID:(3, 0)
Referencia de medición de largos
Descripción 
Cada medición corresponde a una comparación de valor determinado y un patrón de referencia con lo que se obtiene el valor en la unidad correspondiente.
Los patrones han ido cambiando en el tiempo logrando cada vez una mayor exactitud. Ejemplos son:

Copia falsa del primer estándar metro (nótese la ortografía incorrecta), sellada en los cimientos de un edificio, 36 rue de Vaugirard, París, Ken Eckert (Wikimedia Commons)
Una copia del metro provisional instalado de 1796 a 1797, ubicado en la pared de un edificio, 36 rue de Vaugirard, París

Réplicas históricas holandesas de estándares métricos en la colección del Rijksmuseum, Amsterdam: medidor de hierro con caja (construido por Étienne Lenoir, 1799; número de catálogo NG-2001-16-C-8), kilogramo de tumba de cobre con caja (1798; número de catálogo NG-2001-16-D-9), medidas de volumen de cobre ( 1829; número de catálogo NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
En 1799, Étienne Lenoir fabricó los estándares de platino y doce de hierro del metro.

Rule (Modificado de Wikimedia Commons, una regla que representa dos unidades habituales de longitud, el centímetro y la pulgada)
La regla graduada incluye una escala graduada longitudinal fabricadas en acero inoxidable para evitar que la formación de óxido dificulte la lectura o borre la escala.
ID:(2238, 0)
Regla o cinta métrica
Descripción 
Una regla o una cinta métrica son ambos métodos para medir la longitud. Una regla es un dispositivo de medición plano marcado con unidades de longitud como pulgadas, centímetros o milímetros. Una cinta métrica es un dispositivo de medición flexible marcado con unidades de longitud. Las cintas métricas suelen ser más precisas que las reglas, ya que pueden medir superficies curvas y se pueden extender a mayores longitudes.

ID:(12508, 0)
Localizador Laser
Descripción 
Un láser de medición es un dispositivo que utiliza un rayo láser para medir la distancia entre dos puntos. Funciona enviando un pulso láser, que es reflejado por el objeto que se está midiendo y luego detectado por el láser de medición. El tiempo que tarda el pulso láser en viajar desde el láser de medición hasta el objeto y de vuelta se puede usar para calcular la distancia entre los dos puntos. Los láseres de medición se utilizan comúnmente en topografía, navegación y otras aplicaciones en las que se necesitan mediciones precisas.

ID:(481, 0)
GPS (Sistema de Posicionamiento Global)
Descripción 
El Sistema de Posicionamiento Global (GPS) es un sistema de navegación basado en satélites que usa una red de 24 satélites orbitando la Tierra para determinar la ubicación exacta de una persona o objeto en el planeta. Los receptores GPS calculan la distancia a cada satélite midiendo la cantidad de tiempo que tardan las señales en viajar desde el satélite hasta el receptor. Una vez que estas distancias se conocen, el receptor puede usar un proceso llamado trilateración para calcular su ubicación exacta, incluyendo la longitud y la latitud, así como la altitud. Esto se puede usar para medir distancias entre dos ubicaciones, así como la longitud de un camino recorrido por una persona o objeto.

ID:(474, 0)
Posición
Descripción 
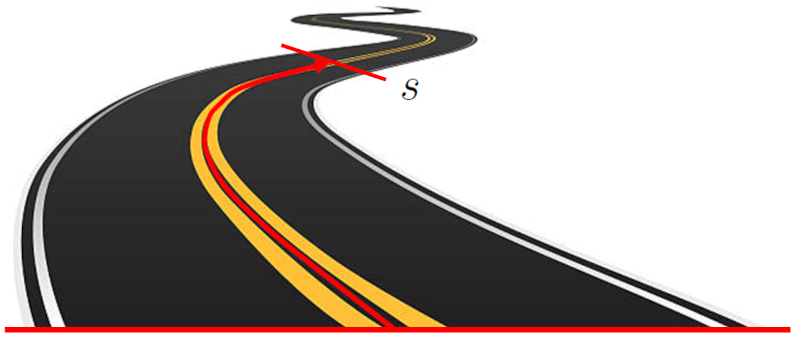
La posición ($s$) de un objeto en un sistema unidimensional se refiere a la ubicación del objeto en relación con un punto de referencia. Esta ubicación se expresa como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta en un eje cartesiano, o puede seguir un camino curvo:
ID:(15, 0)
Posición inicial
Descripción 
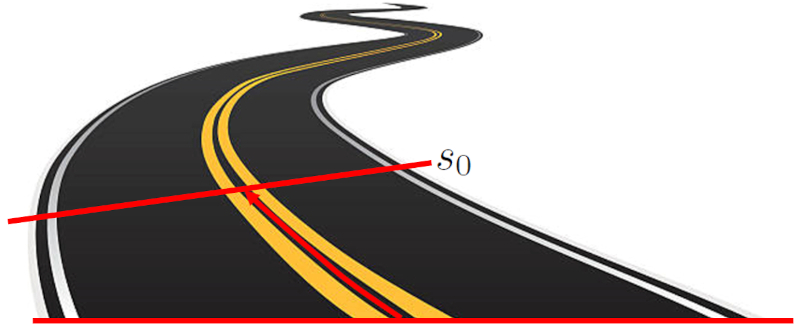
La posición inicial ($s_0$) es la ubicación inicial de un objeto antes de que comience un movimiento. Esta ubicación se define como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta sobre un eje cartesiano, o puede seguir una trayectoria curva.
ID:(10302, 0)
Distancia recorrida
Descripción 
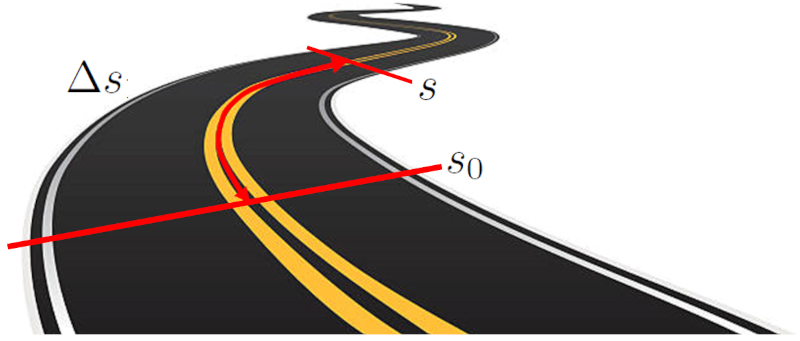
La distancia recorrida en un tiempo ($\Delta s$) por un objeto se mide midiendo la distancia entre dos puntos específicos a lo largo de una trayectoria. Esta trayectoria puede ser una línea recta en un eje cartesiano, o bien un camino curvo. La distancia se calcula midiendo la longitud de la trayectoria entre los dos puntos de partida y llegada.
ID:(9495, 0)
Posición en una dimensión
Modelo 
Para determinar la posición de un objeto, se introduce un sistema de coordenadas que permite establecer un punto de origen y definir la posición mediante la medición de la distancia a lo largo de una línea recta o una curva. Por tanto, la unidad de posición corresponde a una longitud, como kilómetros, metros, centímetros, y así sucesivamente. La elección del sistema de coordenadas es flexible y se busca con el propósito de simplificar al máximo la modelación y los cálculos asociados. Por ejemplo, si el objeto se desplaza a lo largo de una vía, que no necesariamente es recta, es conveniente definir el sistema de coordenadas a lo largo de esa vía. En este caso particular, la posición se define como la distancia desde el origen o el punto de inicio de la vía.
Variables
Cálculos
Cálculos
Ecuaciones
Si se parte de la posición inicial ($s_0$) y se desea calcular la distancia recorrida en un tiempo ($\Delta s$), es necesario definir un valor para la posición ($s$).
En un sistema unidimensional, la distancia recorrida en un tiempo ($\Delta s$) se obtiene simplemente restando la posición inicial ($s_0$) de la posición ($s$), lo que da como resultado:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Ejemplos
Para modelar el movimiento de un cuerpo es necesario describir c mo se desplaza, es decir, el camino y la direcci n en que se mueve. Si el camino es curvo, el vector entre la posici n actual y la futura no necesariamente coincidir con el camino real, a menos que el camino sea infinitesimal. En dicho caso, la desviaci n del segmento es despreciable y el arco corresponde al vector tangencial a la curva.
(ID 14452)
(ID 14449)
La distancia infinitesimal recorrida ($ds$) entre dos puntos es una medida de distancia tan peque a que el movimiento entre ambos puntos puede ser considerado uniforme o sea a velocidad constante.
En general, las diferencias de una variable se denotan a adiendo el s mbolo $\Delta$ antes de la letra correspondiente, de modo que la variaci n de la posici n $s$ se expresa como $\Delta s$. Para variaciones infinitesimales, se utiliza una $d$ en lugar de $\Delta$, por lo que una variaci n infinitesimal en la posici n ser a $ds$.
(ID 14451)
ID:(607, 0)
