Utilisateur:
Loi du levier
Modèle 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
(ID 3241)
(ID 3241)
Dans le cas d'une balance, une force gravitationnelle agit sur chaque bras, g n rant un couple
| $ T = r F $ |
Si les longueurs des bras sont $d_i$ et les forces sont $F_i$ avec $i=1,2$, la condition d' quilibre exige que la somme des couples soit nulle :
| $\displaystyle\sum_i \vec{T}_i=0$ |
Par cons quent, en consid rant que le signe de chaque couple d pend de la direction dans laquelle il induit une rotation,
$d_1F_1-d_2F_2=0$
ce qui donne comme r sultat
.
(ID 3250)
(ID 4431)
(ID 4431)
Exemples
(ID 15845)
tant donn que le couple g n r par la force gravitationnelle et le bras de levier est
| $ T = r F $ |
de chaque c t de la balance, il doit s'annuler en cas d' quilibre pour atteindre l' quilibre :
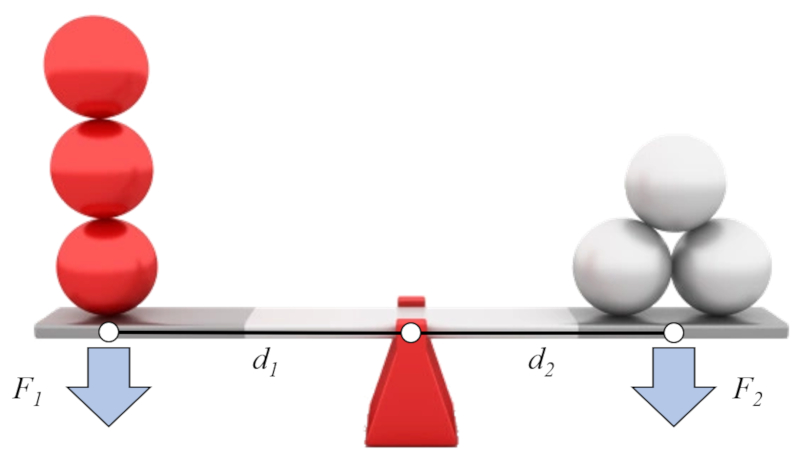
Si l'on suppose que d'un c t , nous avons a forcer 1 ($F_1$) et a force de distance - axe (bras) 1 ($d_1$), et de l'autre c t a forcer 2 ($F_2$) et a force de distance - axe (bras) 2 ($d_2$), on peut tablir la loi dite du levier comme suit :
| $ d_1 F_1 = d_2 F_2 $ |
(ID 15847)
(ID 15846)
ID:(1457, 0)