Utilizador:
Força de uma mola
Storyboard 
A força gerada por uma mola é diretamente proporcional à sua elongação.
A constante de proporcionalidade é chamada de constante da mola ou constante de Hooke. Da mesma forma, a relação dessa força é chamada de Lei de Hooke.
ID:(1414, 0)
Força de uma mola
Descrição
A força gerada por uma mola é diretamente proporcional à sua elongação. A constante de proporcionalidade é chamada de constante da mola ou constante de Hooke. Da mesma forma, a relação dessa força é chamada de Lei de Hooke.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
(ID 3207)
(ID 3241)
Dado que o momento ($p$) se define con la massa inercial ($m_i$) y la velocidade ($v$),
| $ p = m_i v $ |
Si la massa inercial ($m_i$) igual a la massa inicial ($m_0$), ent o podemos derivar o momento em rela o ao tempo e obter la força com massa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Portanto, chegamos conclus o de que
| $ F = m_i a $ |
(ID 10975)
Como la força com massa constante ($F$) igual a la força elástica ($F_k$) menos la força gravitacional ($F_g$):
| $ F = F_k - F_g $ |
Se considerarmos que la força com massa constante ($F$) com la massa inercial ($m_i$) e la aceleração instantânea ($a$)
| $ F = m_i a $ |
e que la força elástica ($F_k$) com la constante de Hooke ($k$) e la alongamento ($u$)
| $ F_k = k x $ |
e que la força gravitacional ($F_g$) com la massa gravitacional ($m_g$) e la aceleração gravitacional ($g$)
| $ F_g = m_g g $ |
ent o resulta
| $ m_i a = k x - m_g g $ |
(ID 11293)
(ID 12338)
(ID 12552)
(ID 15560)
Exemplos
(ID 15521)
Uma mola um fio enrolado que pode ser esticado ou comprimido.
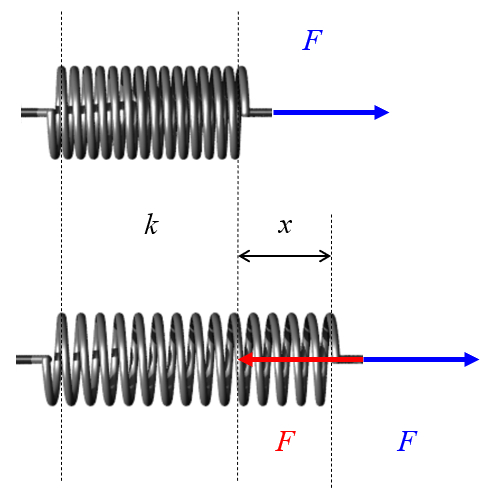
Ao aplicar essas deforma es, a mola gera uma for a que se op e ao movimento.
(ID 12527)
Se a for a necess ria para alcan ar uma determinada elonga o na mola for medida, perceber que ambas s o proporcionais:
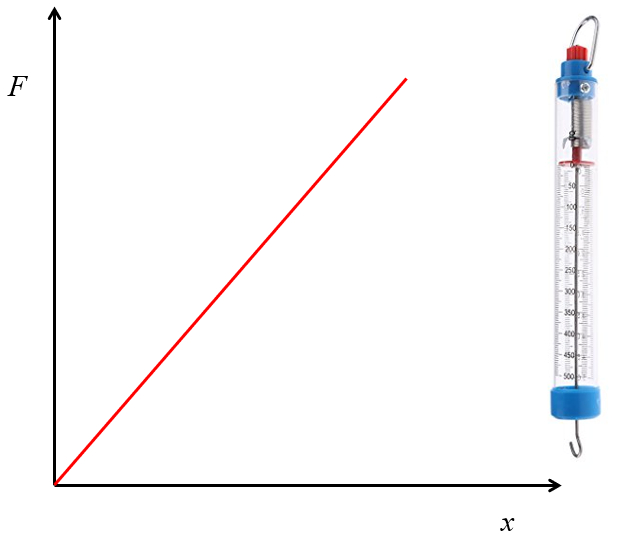
A mola pendurada verticalmente e pesos conhecidos s o adicionados a ela. A elonga o resultante medida e um gr fico de for a versus elonga o tra ado. A inclina o dessa rela o, conhecida como constante el stica da mola ou constante de Hooke, depende das propriedades da mola.
A linearidade dessa rela o permite o uso de molas como um m todo para medir for as.
A for a pode ser medida usando uma mola, estabelecendo uma escala proporcional elonga o que indica diretamente a for a associada.
O instrumento usado para medir for as usando uma mola chamado de dinam metro (a 'dina' a unidade de for a no sistema cgs - cent metros, gramas, segundos - de modo que 10^5 dinas equivalem a um Newton).
(ID 11530)
Para estudar como a mola se alonga, ela pode ser suspensa verticalmente e gradualmente carregada com pesos conhecidos.
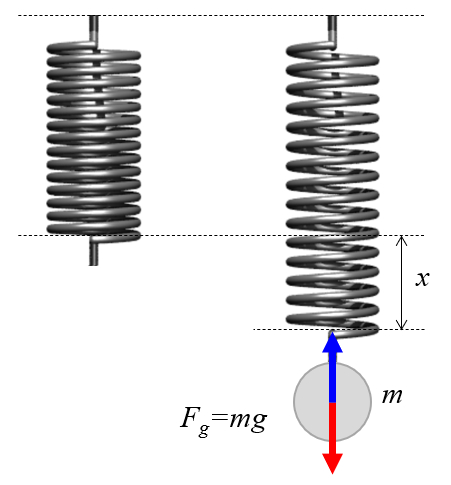
(ID 12528)
(ID 15533)
ID:(1414, 0)