User:
Lever Law
Description 
The lever law corresponds to a system exposed to two equal and opposite torques with which the system remains in equilibrium.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
(ID 3241)
(ID 3241)
In the case of a balance, a gravitational force acts on each arm, generating a torque
| $ T = r F $ |
If the lengths of the arms are $d_i$ and the forces are $F_i$ with $i=1,2$, the equilibrium condition requires that the sum of the torques be zero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Therefore, considering that the sign of each torque depends on the direction in which it induces rotation,
$d_1F_1-d_2F_2=0$
which results in
| $ d_1 F_1 = d_2 F_2 $ |
.
(ID 3250)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Examples
(ID 15845)
Since the torque generated by the gravitational force and the lever arm is
| $ T = r F $ |
on each side of the balance, it must cancel out in the case of equilibrium to achieve balance:
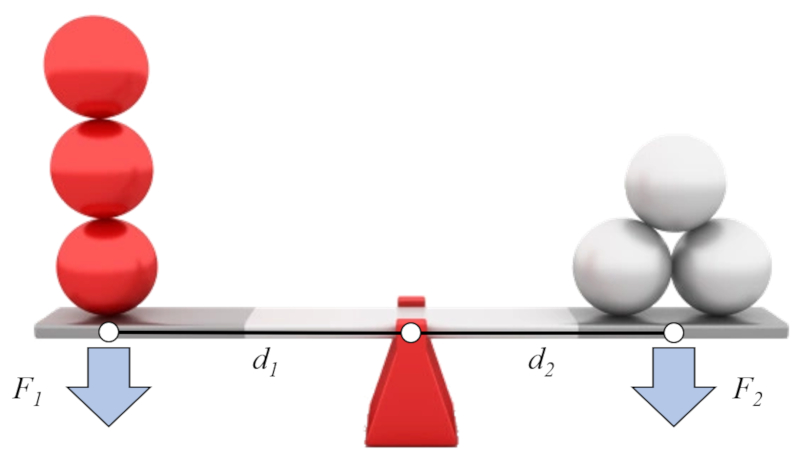
If we assume that on one side we have the force 1 ($F_1$) and the force - axis distance (arm) 1 ($d_1$), and on the other side the force 2 ($F_2$) and the force - axis distance (arm) 2 ($d_2$), we can establish the well-known lever law as follows:
| $ d_1 F_1 = d_2 F_2 $ |
(ID 15847)
(ID 15846)
If a bar mounted on a point acting as a pivot is subjected to the force 1 ($F_1$) at the force - axis distance (arm) 1 ($d_1$) from the pivot, generating a torque $T_1$, and to the force 2 ($F_2$) at the force - axis distance (arm) 2 ($d_2$) from the pivot, generating a torque $T_2$, it will be in equilibrium if both torques are equal. Therefore, the equilibrium corresponds to the so-called law of the lever, expressed as:
| $ d_1 F_1 = d_2 F_2 $ |
(ID 3250)
Since the relationship between angular momentum and torque is
| $ L = r p $ |
its temporal derivative leads us to the torque relationship
| $ T = r F $ |
The body's rotation occurs around an axis in the direction of the torque, which passes through the center of mass.
(ID 4431)
Since the relationship between angular momentum and torque is
| $ L = r p $ |
its temporal derivative leads us to the torque relationship
| $ T = r F $ |
The body's rotation occurs around an axis in the direction of the torque, which passes through the center of mass.
(ID 4431)
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
| $ F_g = m_g g $ |
(ID 3241)
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
| $ F_g = m_g g $ |
(ID 3241)
ID:(1457, 0)