Vitesse constante, deux étapes
Storyboard 
Si lors d'un mouvement à vitesse constante un changement survient, cela résulte en un mouvement qui se déroule en deux étapes, chacune caractérisée par une vitesse définie.
Chaque étape est modélisée par une relation linéaire représentée par une droite, où la clé réside dans le fait que le temps et la position finaux de la première étape sont, à leur tour, le temps et la position initiaux de la deuxième étape.
Il est important de noter que ce modèle présente un problème, car la vitesse change de manière instantanée, ce qui équivaut à une accélération suivie d'un freinage infini, ce qui n'est pas réaliste. Cependant, ce problème n'est pas pertinent si la durée des étapes est considérablement plus longue que le temps pendant lequel le changement de vitesse se produit.
ID:(1448, 0)
Vitesse constante, deux étapes
Storyboard 
Si lors d'un mouvement à vitesse constante un changement survient, cela résulte en un mouvement qui se déroule en deux étapes, chacune caractérisée par une vitesse définie.
Chaque étape est modélisée par une relation linéaire représentée par une droite, où la clé réside dans le fait que le temps et la position finaux de la première étape sont, à leur tour, le temps et la position initiaux de la deuxième étape.
Variables
Calculs
Calculs
Équations
Avec a distance parcourue en un temps ($\Delta s$) c'est avec a position ($s$) et a vitesse ($s_0$) :
et le temps écoulé ($\Delta t$) est avec le temps ($t$) et le temps initial ($t_0$) :
L' quation pour la vitesse moyenne :
peut tre crite comme :
donc, en la r solvant, on obtient :
Avec a distance parcourue en un temps ($\Delta s$) c'est avec a position ($s$) et a vitesse ($s_0$) :
et le temps écoulé ($\Delta t$) est avec le temps ($t$) et le temps initial ($t_0$) :
L' quation pour la vitesse moyenne :
peut tre crite comme :
donc, en la r solvant, on obtient :
Exemples
Le mod le de vitesse constante d crit le mouvement pendant une phase ou un intervalle de temps au cours duquel la vitesse de lobjet peut tre consid r e comme constante. Cependant, un mouvement plus complexe peut inclure plusieurs phases ou intervalles durant lesquels la vitesse varie, voire sinverse (devient n gative), ce qui signifie que lobjet fait marche arri re.
Si lon assemble deux mod les de vitesse constante comme des mouvements cons cutifs, on peut les relier en faisant co ncider les positions et les temps finaux de la premi re phase avec les positions et les temps initiaux du second mouvement. Ainsi, on obtient les distances a distance parcourue lors de la première étape ($\Delta s_1$) et a distance parcourue lors de la deuxième étape ($\Delta s_2$), parcourues avec les vitesses a vitesse du premier étage ($v_1$) et a vitesse du deuxième étage ($v_2$). Ces valeurs peuvent tre modifi es, y compris en inversant le mouvement avec des vitesses n gatives et en lan ant la simulation avec le bouton 'start'.
Dans le cas d'un mouvement se produisant en deux tapes, tout d'abord, l'objet avance une distance de une distance parcourue lors de la première étape ($\Delta s_1$) pendant une p riode de temps de un temps écoulé dans la première étape ($\Delta t_1$) avec une vitesse de une vitesse du premier étage ($v_1$).
Ensuite, dans une deuxi me tape, il avance une distance de une distance parcourue lors de la deuxième étape ($\Delta s_2$) pendant une p riode de temps de un temps passé dans la deuxième étape ($\Delta t_2$) avec une vitesse de une vitesse du deuxième étage ($v_2$).
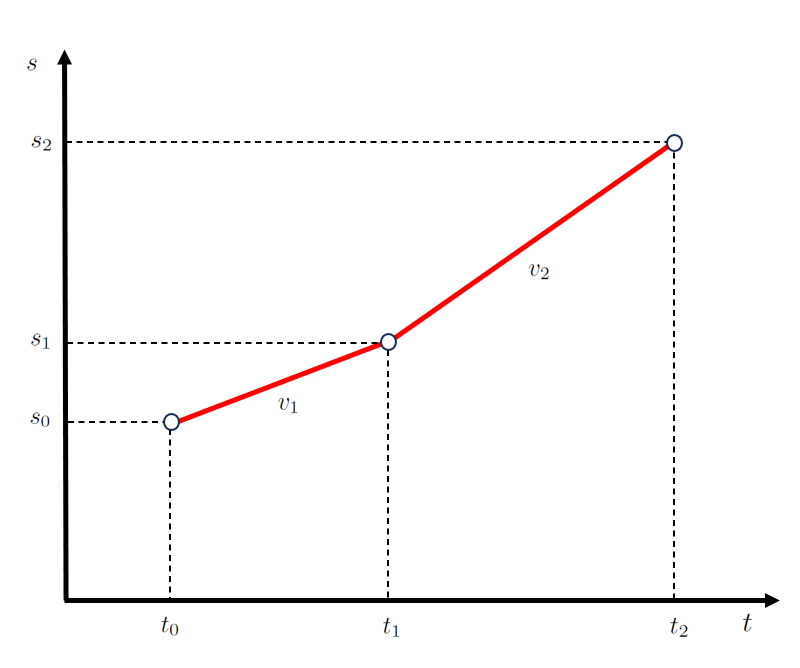
Lorsqu'il est repr sent graphiquement, nous obtenons un diagramme de position-temps comme suit :
Le point cl noter est que le temps écoulé dans la première étape ($\Delta t_1$) et le temps passé dans la deuxième étape ($\Delta t_2$) sont s quentiels, tout comme a distance parcourue lors de la première étape ($\Delta s_1$) et a distance parcourue lors de la deuxième étape ($\Delta s_2$).
Dans le cas d'un mouvement se produisant en deux tapes, tout d'abord, l'objet avance une distance de une distance parcourue lors de la première étape ($\Delta s_1$) pendant une p riode de temps de un temps écoulé dans la première étape ($\Delta t_1$) avec une vitesse de une vitesse du premier étage ($v_1$).
Ensuite, dans une deuxi me tape, il avance une distance de une distance parcourue lors de la deuxième étape ($\Delta s_2$) pendant une p riode de temps de un temps passé dans la deuxième étape ($\Delta t_2$) avec une vitesse de une vitesse du deuxième étage ($v_2$).
Lorsqu'il est repr sent graphiquement, nous obtenons un diagramme de position-temps comme suit :
Le point cl noter est que le temps écoulé dans la première étape ($\Delta t_1$) et le temps passé dans la deuxième étape ($\Delta t_2$) sont s quentiels, tout comme a distance parcourue lors de la première étape ($\Delta s_1$) et a distance parcourue lors de la deuxième étape ($\Delta s_2$).
Dans le cas d'un mouvement en deux tapes, la premi re tape peut tre d crite par une fonction impliquant les points le temps initial ($t_0$), le temps final de la première et départ de la deuxième étape ($t_1$), a vitesse ($s_0$) et le première position finale et départ de la deuxième étape ($s_1$), repr sent e par une droite avec une pente de a vitesse du premier étage ($v_1$):
Pour la deuxi me tape, d finie par les points le première position finale et départ de la deuxième étape ($s_1$), a position finale de la deuxième étape ($s_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), une deuxi me droite avec une pente de a vitesse du deuxième étage ($v_2$) est utilis e:
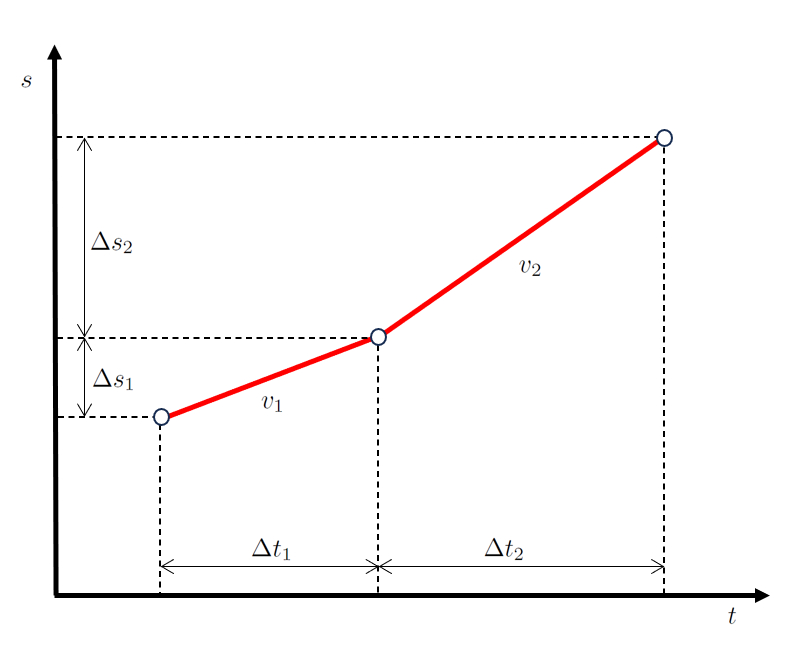
qui est repr sent e comme suit:
Il est important de noter que le d but de la deuxi me tape, d fini par les points le temps final de la première et départ de la deuxième étape ($t_1$) et le première position finale et départ de la deuxième étape ($s_1$), co ncide avec la fin de la premi re tape.
Le mod le de base implique deux mouvements en tapes cons cutives.
Dans la premi re tape, il commence a vitesse ($s_0$) et se termine le première position finale et départ de la deuxième étape ($s_1$), couvrant une distance de a distance parcourue lors de la première étape ($\Delta s_1$), qui commence le temps initial ($t_0$) et se termine le temps final de la première et départ de la deuxième étape ($t_1$), avec une dur e de le temps écoulé dans la première étape ($\Delta t_1$) et une vitesse de a vitesse du premier étage ($v_1$).
Dans la deuxi me tape, il commence le première position finale et départ de la deuxième étape ($s_1$) et se termine a position finale de la deuxième étape ($s_2$), couvrant une distance de a distance parcourue lors de la deuxième étape ($\Delta s_2$), qui commence le temps final de la première et départ de la deuxième étape ($t_1$) et se termine le heure de fin de la deuxième étape ($t_2$), avec une dur e de a distance parcourue lors de la deuxième étape ($\Delta s_2$) et une vitesse de a vitesse du deuxième étage ($v_2$).
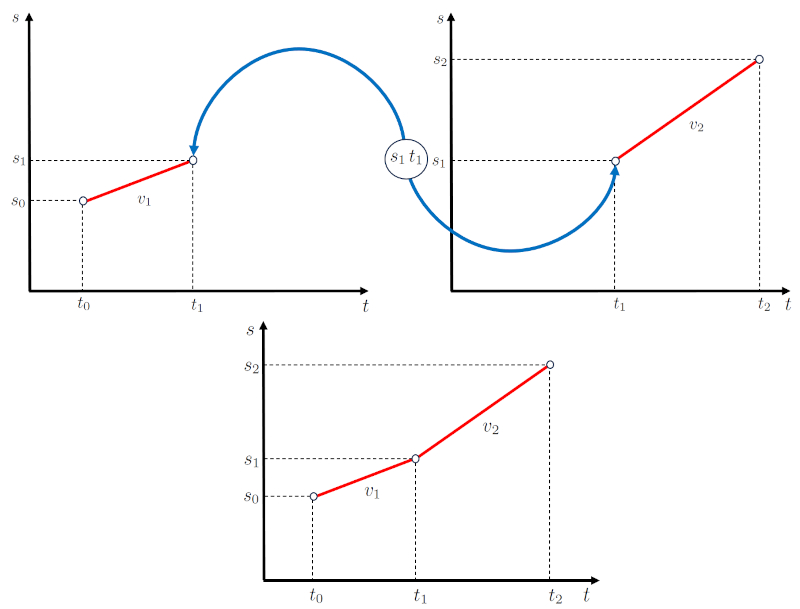
Le diagramme r sultant se compose de deux sous-diagrammes dans lesquels la vitesse est maintenue constante. Les deux diagrammes sont connect s par le première position finale et départ de la deuxième étape ($s_1$) et le temps final de la première et départ de la deuxième étape ($t_1$), qui correspondent au point final de la premi re tape et au point de d part de la deuxi me tape.
Ainsi, la structure en r seau du mod le est la suivante :
Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) partir de a vitesse ($s_0$) et a position ($s$) gr ce l' quation suivante :
Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) partir de a vitesse ($s_0$) et a position ($s$) gr ce l' quation suivante :
Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :
Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :
A vitesse moyenne ($\bar{v}$) peut tre calcul partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) en utilisantxa0:
A vitesse moyenne ($\bar{v}$) peut tre calcul partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) en utilisantxa0:
Si la vitesse est constante, la vitesse sera gale a vitesse initiale ($v_0$). Dans ce cas, la distance parcourue en fonction du temps peut tre calcul e en utilisant la diff rence entre a position ($s$) et a vitesse ($s_0$), divis e par la diff rence entre le temps ($t$) et le temps initial ($t_0$) :
L' quation correspondante d finit une ligne droite dans l'espace-temps.
Si la vitesse est constante, la vitesse sera gale a vitesse initiale ($v_0$). Dans ce cas, la distance parcourue en fonction du temps peut tre calcul e en utilisant la diff rence entre a position ($s$) et a vitesse ($s_0$), divis e par la diff rence entre le temps ($t$) et le temps initial ($t_0$) :
L' quation correspondante d finit une ligne droite dans l'espace-temps.
ID:(1448, 0)