Énergie cinétique totale
Storyboard 
L'énergie cinétique totale est la somme de l'énergie cinétique de translation et de l'énergie cinétique de rotation.Cette distinction est importante car selon la manière dont un objet se déplace, l'énergie cinétique peut être distribuée différemment entre la translation et la rotation, ce qui affecte la vitesse à laquelle il se déplace.
ID:(1418, 0)
Cylindre qui tourne autour de l'axe $\parallel$
Image 
Considérons une rotation d'un cylindre de masse $m$ et de rayon $r$ autour de l'axe du cylindre, où le centre de masse (CM) se situe à mi-hauteur :
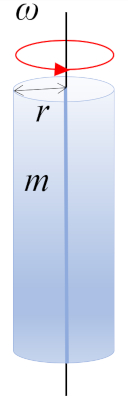
ID:(10964, 0)
Sphère
Image 
Une sphère de masse $m$ et de rayon $r$ tourne autour de son centre de masse, qui est situé au centre de celle-ci :
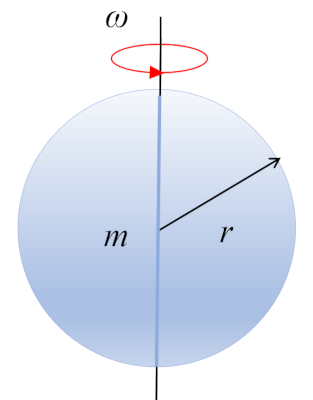
ID:(10490, 0)
Énergie cinétique totale
Modèle 
L'énergie cinétique totale est la somme de l'énergie cinétique de translation et de l'énergie cinétique de rotation. Cette distinction est importante car selon la manière dont un objet se déplace, l'énergie cinétique peut être distribuée différemment entre la translation et la rotation, ce qui affecte la vitesse à laquelle il se déplace.
Variables
Calculs
Calculs
Équations
L' nergie n cessaire pour qu'un objet passe de la vitesse angulaire $\omega_1$ la vitesse angulaire $\omega_2$ peut tre calcul e l'aide de la d finition
| $ \Delta W = T \Delta\theta $ |
Avec la deuxi me loi de Newton, nous pouvons r crire cette expression comme
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
En utilisant la d finition de la vitesse angulaire
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
nous obtenons
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I,\omega,\Delta\omega$
La diff rence entre les vitesses angulaires est
$\Delta\omega=\omega_2-\omega_1$
D'autre part, la vitesse angulaire elle-m me peut tre approxim e par la vitesse angulaire moyenne
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
En utilisant ces deux expressions, nous obtenons l' quation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Ainsi, l' nergie varie selon
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Nous pouvons utiliser cela pour d finir l' nergie cin tique
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
(ID 3244)
A écart de travail ($\Delta W$) nécessaire pour quun objet passe de a vitesse angulaire initiale ($\omega_0$) à A vitesse angulaire ($\omega$) est obtenue en appliquant un a torque ($T$) qui produit un déplacement angulaire a différence d'angles ($\Delta\theta$), selon :
| $ \Delta W = T \Delta\theta $ |
En appliquant la deuxième loi de Newton pour la rotation, avec a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) et a accélération angulaire moyenne ($\bar{\alpha}$) :
| $ T = I \alpha $ |
cette expression peut être réécrite comme :
$\Delta W = I \alpha \Delta\theta$
ou, en utilisant a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$) :
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
nous obtenons :
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
En utilisant la définition de a vitesse angulaire moyenne ($\bar{\omega}$) et le temps écoulé ($\Delta t$) :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
il en résulte :
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
où A différence de vitesses angulaires ($\Delta\omega$) sexprime comme :
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Dautre part, la vitesse angulaire peut être approximée par la vitesse angulaire moyenne :
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
En combinant les deux expressions, on obtient léquation :
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Ainsi, la variation dénergie sexprime comme :
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Cela permet de définir lénergie cinétique de rotation comme :
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 3686)
Lorsqu'un objet roule, sa vitesse angulaire est reli e sa vitesse de translation par
| $ v = r \omega $ |
ce qui entra ne l' nergie cin tique de rotation
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
qui devient
$K_r=\displaystyle\frac{1}{2}I \omega^2=\displaystyle\frac{1}{2} I \displaystyle\frac{v^2}{r^2}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{I}{r^2}\right)v^2$
Ainsi, en combinant l' nergie cin tique de translation
l' nergie cin tique d'un corps en rotation est calcul e par la somme
| $ K = K_t + K_r $ |
c'est- -dire,
| $ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$ |
(ID 9877)
A énergie cinétique totale ($K$) correspond à la somme de a énergie cinétique translationnelle ($K_t$) et a énergie cinétique de rotation ($K_r$) :
| $ K = K_t + K_r $ |
Étant donné que a énergie cinétique translationnelle ($K_t$) sexprime en fonction de a masse d'inertie ($m_i$) et a vitesse ($v$) :
| $ K_t =\displaystyle\frac{1}{2} m v ^2$ |
et que a énergie cinétique de rotation ($K_r$), en fonction de a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) et a vitesse angulaire ($\omega$), se définit comme :
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
on obtient alors lexpression finale :
| $ K =\displaystyle\frac{1}{2} m_i v ^2+\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 9944)
Exemples
(ID 15605)
(ID 15607)
ID:(1418, 0)
