Velocidade constante, dois estágios
Storyboard 
Se durante um movimento a uma velocidade constante ocorre uma mudança, isso resulta em um movimento que acontece em duas etapas, cada uma caracterizada por uma velocidade definida.
Cada etapa é modelada com uma relação linear representada por uma reta, onde a chave está no fato de que o tempo e a posição finais da primeira etapa são, por sua vez, o tempo e a posição iniciais da segunda etapa.
É importante notar que este modelo apresenta um problema, já que a velocidade muda de forma instantânea, o que equivale a uma aceleração seguida de uma desaceleração infinita, o que não é realista. No entanto, este problema não é relevante se a duração das etapas for consideravelmente mais longa do que o tempo em que ocorre a mudança de velocidade.
ID:(1448, 0)
Mecanismos
Definição 
Na primeira etapa, se a velocidade for constante, estabelece-se uma relação direta de la velocidade do primeiro estágio ($v_1$) entre o primeira posição final e largada na segunda etapa ($s_1$) e o tempo final da primeira e início da segunda etapa ($t_1$), representada por uma linha reta.
Na segunda etapa, não podem ser definidas posições e tempos iniciais nulos, pois devem corresponder a o primeira posição final e largada na segunda etapa ($s_1$) e o tempo final da primeira e início da segunda etapa ($t_1$). Uma vez que a velocidade é constante nesta etapa, estabelece-se uma relação direta de la velocidade do segundo estágio ($v_2$) entre la posição final da segunda fase ($s_2$) e o hora de término da segunda etapa ($t_2$), representada por outra linha reta.
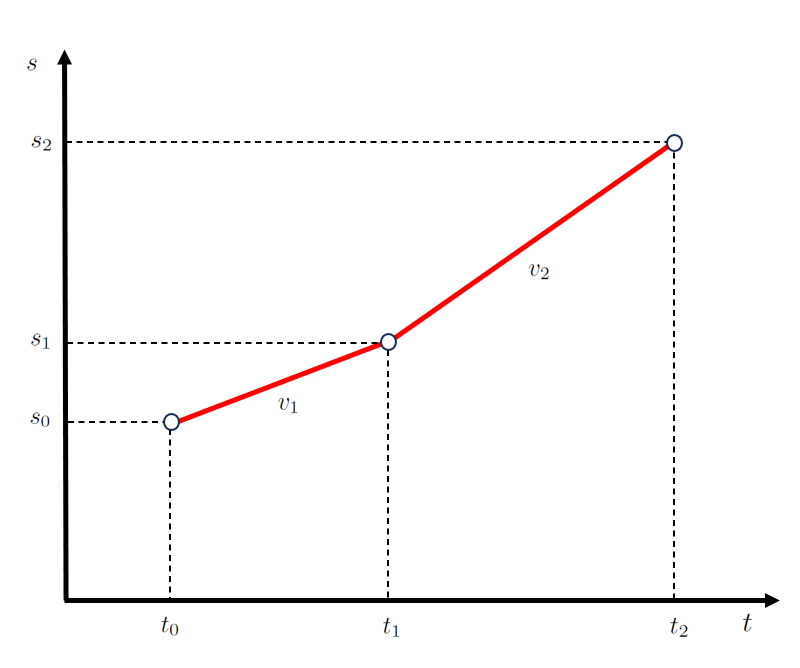
qual é a chave do modelo representado pela rede:
ID:(15383, 0)
Conceito de dois estágios
Imagem 
No caso de um movimento ocorrendo em duas etapas, primeiro, o objeto avança uma distância de uma distância percorrida na primeira etapa ($\Delta s_1$) durante um período de tempo de um tempo decorrido na primeira etapa ($\Delta t_1$) com uma velocidade de uma velocidade do primeiro estágio ($v_1$).
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
Então, em uma segunda etapa, ele avança uma distância de uma distância percorrida na segunda etapa ($\Delta s_2$) durante um período de tempo de um tempo gasto na segunda etapa ($\Delta t_2$) com uma velocidade de uma velocidade do segundo estágio ($v_2$).
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
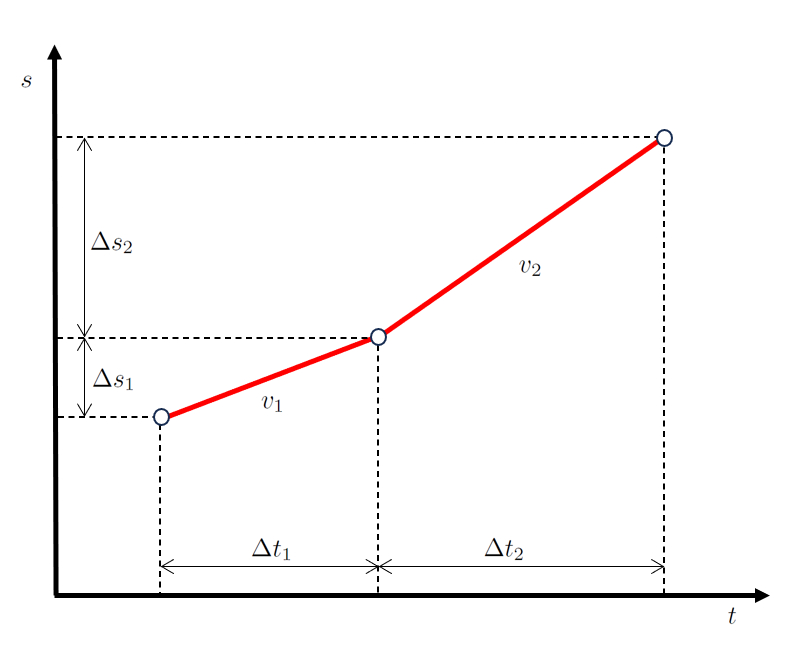
Quando representado graficamente, obtemos um diagrama de posição-tempo como segue:
O ponto chave a ser observado é que o tempo decorrido na primeira etapa ($\Delta t_1$) e o tempo gasto na segunda etapa ($\Delta t_2$) são sequenciais, assim como la distância percorrida na primeira etapa ($\Delta s_1$) e la distância percorrida na segunda etapa ($\Delta s_2$).
ID:(15504, 0)
Velocidades em dois estágios
Nota 
No caso de um movimento ocorrendo em duas etapas, primeiro, o objeto avança uma distância de uma distância percorrida na primeira etapa ($\Delta s_1$) durante um período de tempo de um tempo decorrido na primeira etapa ($\Delta t_1$) com uma velocidade de uma velocidade do primeiro estágio ($v_1$).
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
Então, em uma segunda etapa, ele avança uma distância de uma distância percorrida na segunda etapa ($\Delta s_2$) durante um período de tempo de um tempo gasto na segunda etapa ($\Delta t_2$) com uma velocidade de uma velocidade do segundo estágio ($v_2$).
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
Quando representado graficamente, obtemos um diagrama de posição-tempo como segue:
O ponto chave a ser observado é que o tempo decorrido na primeira etapa ($\Delta t_1$) e o tempo gasto na segunda etapa ($\Delta t_2$) são sequenciais, assim como la distância percorrida na primeira etapa ($\Delta s_1$) e la distância percorrida na segunda etapa ($\Delta s_2$).
ID:(15395, 0)
Posições e horários em duas etapas
Citar 
No caso de um movimento em duas etapas, a primeira etapa pode ser descrita por uma função que envolve os pontos o tempo inicial ($t_0$), o tempo final da primeira e início da segunda etapa ($t_1$), la velocidade ($s_0$) e o primeira posição final e largada na segunda etapa ($s_1$), representada por uma reta com uma inclinação de la velocidade do primeiro estágio ($v_1$):
| $ s_1 = s_0 + v_1 ( t_1 - t_0 )$ |
Para a segunda etapa, definida pelos pontos o primeira posição final e largada na segunda etapa ($s_1$), la posição final da segunda fase ($s_2$), o tempo final da primeira e início da segunda etapa ($t_1$) e o hora de término da segunda etapa ($t_2$), é utilizada uma segunda reta com uma inclinação de la velocidade do segundo estágio ($v_2$):
| $ s_2 = s_1 + v_2 ( t_2 - t_1 )$ |
que é representada como:

É importante observar que o início da segunda etapa, definido pelos pontos o tempo final da primeira e início da segunda etapa ($t_1$) e o primeira posição final e largada na segunda etapa ($s_1$), coincide com o final da primeira etapa.
ID:(15396, 0)
Modelo
Exercício 
O modelo básico envolve dois movimentos em etapas consecutivas.
Na primeira etapa, começa em la velocidade ($s_0$) e termina em o primeira posição final e largada na segunda etapa ($s_1$), cobrindo uma distância de la distância percorrida na primeira etapa ($\Delta s_1$), que começa em o tempo inicial ($t_0$) e termina em o tempo final da primeira e início da segunda etapa ($t_1$), com duração de o tempo decorrido na primeira etapa ($\Delta t_1$) e uma velocidade de la velocidade do primeiro estágio ($v_1$).
Na segunda etapa, começa em o primeira posição final e largada na segunda etapa ($s_1$) e termina em la posição final da segunda fase ($s_2$), cobrindo uma distância de la distância percorrida na segunda etapa ($\Delta s_2$), que começa em o tempo final da primeira e início da segunda etapa ($t_1$) e termina em o hora de término da segunda etapa ($t_2$), com duração de la distância percorrida na segunda etapa ($\Delta s_2$) e uma velocidade de la velocidade do segundo estágio ($v_2$).
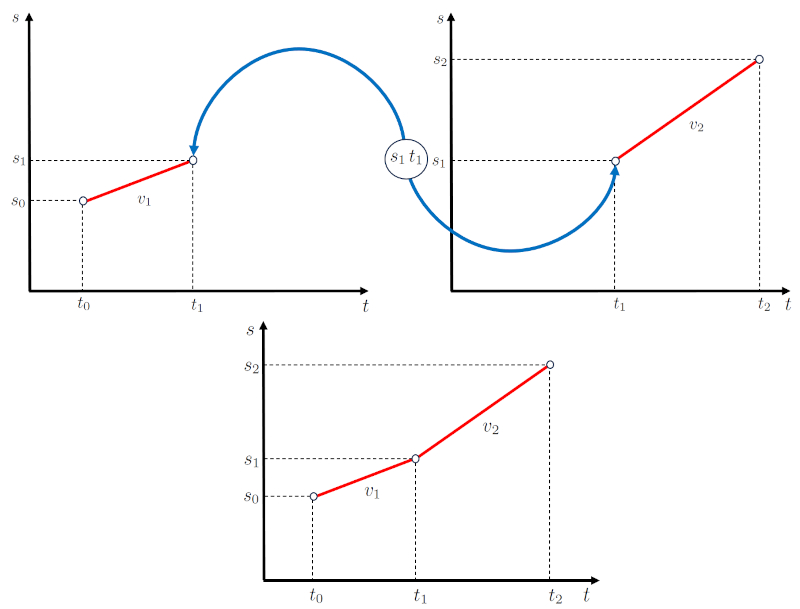
O diagrama resultante consiste em dois subdiagramas nos quais a velocidade é mantida constante. Ambos os diagramas estão conectados por o primeira posição final e largada na segunda etapa ($s_1$) e o tempo final da primeira e início da segunda etapa ($t_1$), que correspondem ao ponto final da primeira etapa e ao ponto inicial da segunda etapa.

Com isso, a estrutura de rede do modelo é a seguinte:
ID:(15384, 0)
Velocidade constante, dois estágios
Storyboard 
Se durante um movimento a uma velocidade constante ocorre uma mudança, isso resulta em um movimento que acontece em duas etapas, cada uma caracterizada por uma velocidade definida.
Cada etapa é modelada com uma relação linear representada por uma reta, onde a chave está no fato de que o tempo e a posição finais da primeira etapa são, por sua vez, o tempo e a posição iniciais da segunda etapa.
Variáveis
Cálculos
Cálculos
Equações
Com la distância percorrida em um tempo ($\Delta s$) com la posição ($s$) e la velocidade ($s_0$):
e o tempo decorrido ($\Delta t$) com o tempo ($t$) e o tempo inicial ($t_0$):
A equa o para a velocidade m dia:
pode ser escrita como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
portanto, resolvendo para ela obtemos:
Com la distância percorrida em um tempo ($\Delta s$) com la posição ($s$) e la velocidade ($s_0$):
e o tempo decorrido ($\Delta t$) com o tempo ($t$) e o tempo inicial ($t_0$):
A equa o para a velocidade m dia:
pode ser escrita como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
portanto, resolvendo para ela obtemos:
Exemplos
O modelo de velocidade constante descreve o movimento durante uma etapa ou intervalo de tempo em que a velocidade do objeto pode ser considerada constante. No entanto, um movimento mais complexo pode envolver v rias etapas ou intervalos nos quais a velocidade varia e pode at se inverter (tornar-se negativa), indicando que o objeto est voltando.
Se dois modelos de velocidade constante forem combinados como movimentos consecutivos, poss vel vincul -los definindo que as posi es e os tempos finais da primeira etapa s o iguais s posi es e aos tempos iniciais do segundo movimento. Dessa forma, definem-se as dist ncias la distância percorrida na primeira etapa ($\Delta s_1$) e la distância percorrida na segunda etapa ($\Delta s_2$), percorridas com as velocidades la velocidade do primeiro estágio ($v_1$) e la velocidade do segundo estágio ($v_2$). Esses valores podem ser modificados, inclusive invertendo o movimento ao definir velocidades negativas e iniciar a simula o com o bot o 'start'.
No caso de um movimento ocorrendo em duas etapas, primeiro, o objeto avan a uma dist ncia de uma distância percorrida na primeira etapa ($\Delta s_1$) durante um per odo de tempo de um tempo decorrido na primeira etapa ($\Delta t_1$) com uma velocidade de uma velocidade do primeiro estágio ($v_1$).
Ent o, em uma segunda etapa, ele avan a uma dist ncia de uma distância percorrida na segunda etapa ($\Delta s_2$) durante um per odo de tempo de um tempo gasto na segunda etapa ($\Delta t_2$) com uma velocidade de uma velocidade do segundo estágio ($v_2$).
Quando representado graficamente, obtemos um diagrama de posi o-tempo como segue:
O ponto chave a ser observado que o tempo decorrido na primeira etapa ($\Delta t_1$) e o tempo gasto na segunda etapa ($\Delta t_2$) s o sequenciais, assim como la distância percorrida na primeira etapa ($\Delta s_1$) e la distância percorrida na segunda etapa ($\Delta s_2$).
No caso de um movimento ocorrendo em duas etapas, primeiro, o objeto avan a uma dist ncia de uma distância percorrida na primeira etapa ($\Delta s_1$) durante um per odo de tempo de um tempo decorrido na primeira etapa ($\Delta t_1$) com uma velocidade de uma velocidade do primeiro estágio ($v_1$).
Ent o, em uma segunda etapa, ele avan a uma dist ncia de uma distância percorrida na segunda etapa ($\Delta s_2$) durante um per odo de tempo de um tempo gasto na segunda etapa ($\Delta t_2$) com uma velocidade de uma velocidade do segundo estágio ($v_2$).
Quando representado graficamente, obtemos um diagrama de posi o-tempo como segue:
O ponto chave a ser observado que o tempo decorrido na primeira etapa ($\Delta t_1$) e o tempo gasto na segunda etapa ($\Delta t_2$) s o sequenciais, assim como la distância percorrida na primeira etapa ($\Delta s_1$) e la distância percorrida na segunda etapa ($\Delta s_2$).
No caso de um movimento em duas etapas, a primeira etapa pode ser descrita por uma fun o que envolve os pontos o tempo inicial ($t_0$), o tempo final da primeira e início da segunda etapa ($t_1$), la velocidade ($s_0$) e o primeira posição final e largada na segunda etapa ($s_1$), representada por uma reta com uma inclina o de la velocidade do primeiro estágio ($v_1$):
Para a segunda etapa, definida pelos pontos o primeira posição final e largada na segunda etapa ($s_1$), la posição final da segunda fase ($s_2$), o tempo final da primeira e início da segunda etapa ($t_1$) e o hora de término da segunda etapa ($t_2$), utilizada uma segunda reta com uma inclina o de la velocidade do segundo estágio ($v_2$):
que representada como:
importante observar que o in cio da segunda etapa, definido pelos pontos o tempo final da primeira e início da segunda etapa ($t_1$) e o primeira posição final e largada na segunda etapa ($s_1$), coincide com o final da primeira etapa.
O modelo b sico envolve dois movimentos em etapas consecutivas.
Na primeira etapa, come a em la velocidade ($s_0$) e termina em o primeira posição final e largada na segunda etapa ($s_1$), cobrindo uma dist ncia de la distância percorrida na primeira etapa ($\Delta s_1$), que come a em o tempo inicial ($t_0$) e termina em o tempo final da primeira e início da segunda etapa ($t_1$), com dura o de o tempo decorrido na primeira etapa ($\Delta t_1$) e uma velocidade de la velocidade do primeiro estágio ($v_1$).
Na segunda etapa, come a em o primeira posição final e largada na segunda etapa ($s_1$) e termina em la posição final da segunda fase ($s_2$), cobrindo uma dist ncia de la distância percorrida na segunda etapa ($\Delta s_2$), que come a em o tempo final da primeira e início da segunda etapa ($t_1$) e termina em o hora de término da segunda etapa ($t_2$), com dura o de la distância percorrida na segunda etapa ($\Delta s_2$) e uma velocidade de la velocidade do segundo estágio ($v_2$).
O diagrama resultante consiste em dois subdiagramas nos quais a velocidade mantida constante. Ambos os diagramas est o conectados por o primeira posição final e largada na segunda etapa ($s_1$) e o tempo final da primeira e início da segunda etapa ($t_1$), que correspondem ao ponto final da primeira etapa e ao ponto inicial da segunda etapa.
Com isso, a estrutura de rede do modelo a seguinte:
Podemos calcular la distância percorrida em um tempo ($\Delta s$) a partir de la velocidade ($s_0$) y la posição ($s$) usando a seguinte equa o:
Podemos calcular la distância percorrida em um tempo ($\Delta s$) a partir de la velocidade ($s_0$) y la posição ($s$) usando a seguinte equa o:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
La velocidade média ($\bar{v}$) pode ser calculado a partir de la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$) usando:
La velocidade média ($\bar{v}$) pode ser calculado a partir de la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$) usando:
Se a velocidade for constante, a velocidade ser igual a la velocidade inicial ($v_0$). Neste caso, o caminho percorrido em fun o do tempo pode ser calculado usando a diferen a entre la posição ($s$) e la velocidade ($s_0$), dividida pela diferen a entre o tempo ($t$) e o tempo inicial ($t_0$):
A equa o correspondente define uma linha reta no espa o-tempo.
Se a velocidade for constante, a velocidade ser igual a la velocidade inicial ($v_0$). Neste caso, o caminho percorrido em fun o do tempo pode ser calculado usando a diferen a entre la posição ($s$) e la velocidade ($s_0$), dividida pela diferen a entre o tempo ($t$) e o tempo inicial ($t_0$):
A equa o correspondente define uma linha reta no espa o-tempo.
ID:(1448, 0)
